Image Source.

If one looks at planetary systems from the “modern” point of view provided by the HARPS survey and the results from Kepler’s recent data release, our own solar system looks pretty strange. In the Sun’s case, the frequently planetiferous orbital zones inside of P=50 days are completely, mysteriously barren. The orbital region inside P<3000 days is also almost entirely bereft, with just a few iron-silicate dregs totaling less than two Earth masses. Out in the boondocks, however, the Sun’s harbors a giant planet that managed to accumulate lots of gas, yet paradoxically didn’t manage to migrate a really significant distance.

It will take more time to determine whether the solar system is really all that weird, but with each passing month’s accumulation of fresh exoplanets, our eight-planet set-up manages to seem slightly less ordinary. Jupiter, for example, induces a 12 m/s velocity half-amplitude, and the high-precision radial velocity surveys have been operating for long enough so that if true-Jupiter analogs were the rule, then we’d perhaps be hearing of more of them being detected.

The Kepler multi-transiting candidates correspond to systems that are completely alien when compared to MVEMJSUN, but they are much more familiar when compared to the regular giant planet satellites — the moon systems of Jupiter, Saturn and Uranus. In each of these cases (and despite a factor-of-twenty difference in mass between Jupiter and Uranus) the characteristic orbital period is of order a week, and the characteristic secondary-to-primary mass ratios are of order a few parts in 100,000. For example, Ariel, Umbriel, Titania and Oberon have mass ratios of 1.6e-5, 1.4e-5, 4.0e-5, and 3.5e-5 relative to Uranus, and their orbital periods are 2.52, 4.14, 8.71, and 13.46 days. In the Jovian system, the satellite/Jupiter ratios for Io, Europa, Ganymede and Callisto are 4.7e-5, 2.5e-5, 7.9e-5, and 5.8e-5, with corresponding orbital periods of 1.76, 3.55, 7.15, and 16.68 days.

In the plot below, I’ve taken the 45 three-transit systems from Kepler’s list, and plotted the orbital periods of their constituent planet candidates along the x-axis. The colors of the points are given a linear gray-scale, with black corresponding to a planet-to-star mass ratio of zero, and white corresponding to a planet-to-star mass ratio of 1.0e-4 or larger. I’ve converted radius to mass by assuming M=R^2 when mass and radius are expressed in Earth masses and Earth radii.

It’s interesting to speculate whether the commonality between the regular satellite systems, and the teeming population of Super-Earth/Sub-Neptune class systems might be more than just a coincidence…

The extrasolar planets constitute a fast-moving field. I was looking at the slides from a talk that I gave in early 2005, in which I showed the then-current, now hopelessly outdated, mass-period diagram for the known extrasolar planets:

At that time, the name “Gliese” had barely edged into the public consciousness, as a Google trends and news reference diagram illustrates:

The discovery of Gliese 436b occurred in the summer of 2004, and was the first Neptune-mass extrasolar planet found. The following summer saw the announcement of the first unambiguous “super-Earth”, Gliese 876d, which generated a blip in search volume in addition to news volume. The discovery of Gliese 876d might have been a bigger story, had it not shared a news cycle with Michael Jackson:

In early 2005, there was essentially no hint of the enormous population of sub-Neptune/super-Earths lying just below the threshold of detectability. Population synthesis models for extrasolar planets were doing an excellent job of reproducing the distribution of hot Jupiters, the period “desert”, and the population of eccentric giants, but at that time, the smart-money expectation was that the pickings would be rather slim in the hot sub-Neptune regime. (It was also believed that the detection rate would pick up substantially once truly terrestrial planets became observable.)

Mayor et al.’s announcement in 2008, therefore, came as a real bombshell. The Geneva Team made the startling claim that a very substantial fraction of stars in the solar neighborhood harbor at least one planet with Neptune mass or less, with an orbital period of fifty days or less. Their claim is equivalent to the statement that in a volume-limited survey, the number of planets in the green box of the diagram below is of order five times greater than the sum of the number in the peach box and the blue box.

In the diagram above, the population of planets known in 2010 is plotted. There’s a bulky cohort of RV-detected eccentric giants (Msin(i)’s), a lot of hot Jupiters from the transit surveys, and a respectable, but still sparse population in the sub-Neptune/super-Earth category. The Geneva claim was based primarily on signals that are emerging in the HARPS data, rather than solid published planets.

Fast-forward to last week. Kepler has suddenly augmented the planetary census by more than a factor of three. If we estimate masses through the simple relation Mpl=Rpl^2, then we can plot the Kepler candidates on the mass-period diagram. Detection biases etc., etc. aside, it’s abundantly clear that there is indeed a huge population of objects in the ground staked out by the Mayor et al. 2008 announcement:

In trying to make sense of the flood of new Kepler results, the very first order of business is to run through the various scatter plots to get a sense for the distributions, to look for correlations, and to test pet theories.

Kevin Schlaufman has made a useful formatted electronic table that joins Tables 1 and 2 from the Borucki et al. (2011) paper. Sifting through this table alone, notwithstanding the gigabytes of light curves currently available for download, there’s lots of very interesting stuff. For example, plotting planetary effective temperature vs planetary radius shows that as expected, there are a lot more small planets than large planets:

If we were looking at a complete volume-limited survey of planets, then this plot would have an interesting interpretation. The downward sweep of the main locus suggests that hot planets, by and large, tend to be smaller than cooler planets. The natural interpretation would be that we’re seeing a signature of evaporation — hence CoRoT-7b, AKA “Planet Freeport-McMoran” is small, whereas Gliese 1214b AKA “Planet Dasani” is relatively large by comparison. (Corporations interested in paying for product placements on oklo.org, please contact me directly.) Sadly, however, before jumping to conclusions, one has to worry about a whole host of possible gotcha-style observational biases. Small planets are harder to detect via transits, meaning that more orbits are required to reach given signal-to-noise, meaning that small planets are more likely to be found on short-period orbits. My gut feeling is that these effects might not be strong enough to completely wipe out the observed correlation, but it’ll take a lot of careful Monte-Carlo work to understand for sure.

I’ve got some unhedged exposure to the planet-stellar mass correlation. The idea is that if core accretion is zeroth-order correct, then it should be easier to form giant planets in orbit around more massive stars. If this hypothesis is correct, then the giant planet fraction (defined as planets having radii greater than 5 Earth radii divided by the total number of planets) should increase as one increases the mass of the host star. Again, if one lives dangerously, throwing caution regarding biases completely to the wind, this seems to be the case with the 1235 Kepler candidates:

The planetary disturbing function describes the time-dependent perturbing potential of one planet acting on another. The disturbing function dictates the non-Keplerian evolution of planetary orbits, and while it’s conceptually simple, it’s a triumph of analysis that it can be written down as a function of the planetary orbital elements themselves.

In large part, celestial mechanics consists of choosing the right terms in the disturbing function for a particular planetary configuration, and then working out the simplified motion that arises from the chosen terms. With this program, phenomena ranging from the “Great Inequality” of Jupiter and Saturn to the possible eventual ejection of Mercury from the Solar System can be isolated and understood.

Wednesday’s Kepler data release spills a nearly overwhelming number of new multiple-planet systems into the public domain. The data include 115 candidate double-transit systems, 45 triples, 8 quads, and one each with five and six transiting planets. Precise timing measurements make all of these set-ups amenable to analysis. Correct case-by-case invocation of the disturbing function, along with an account of tidal dissipation when relevant, will generate a deep understanding of what these planets are doing, and how they got to their present state.

That’s more than a few days work. In the interim, Dan Fabrycky has created a mesmerizing video (click here for the YouTube link) which shows a wide selection of the new multi-planet systems running through their orbits for the duration of the nominal Kepler mission. It’s a multiplexed digital update of the classical clockwork orrerys that mechanically integrated the motion of those old-fashioned planets in our own solar system.

At 5pm PST yesterday afternoon, a series of papers from the Kepler team were released on astro-ph. These include the Borucki et al. overview of the full data set from the first four months of observation, as well as articles that delve more deeply into the results. It’s hard to know quite where to begin. In a field that’s seen more than its share of hype and hyperbole, these papers and the accompanying data represent a watershed. The most interesting facets of the galactic planetary census can now be downloaded onto your hard drive — either in the form of raw light curves or as a ready-mixed compilation of over a thousand planets. I guess it’s time to stay up late…

Earlier this year, while putting together my slides for a UC Berkeley astronomy colloquium, I got the list of asteroid discovery dates from the Minor Planet Center. Back in 1801, the discovery of Ceres was every bit as big a deal as the discovery of the first extrasolar planets, so I thought it would be interesting to compare the progression of the asteroid discoveries with that of the extrasolar planets.

The first four asteroids, 1 Ceres, 2 Pallas, 3 Juno, and 4 Vesta were all discovered within a few years of each other, and then there was a surprisingly long gap until the discovery of 5 Astraea in 1845. Here, (courtesy of the Wikipedia), are the relative sizes of the first 10 asteroids in comparison to the size of Earth’s Moon:

Starting in 1847, asteroid detections began ramping up, and by 1857, there were enough examples for Daniel Kirkwood to notice gaps in the distribution which he (correctly) suspected were due to orbital commensurabilities with Jupiter.

Source: D. Kirkwood, 1867 AAAS Proceedings

With the extrasolar planets, the shape of the discovery histogram is strikingly similar. The pace of events, however, has unfolded five times faster, with the gap between the discovery of HD 114762 b and 51 Peg b being followed by a steady ramp-up in the pace of confirmed detections. There are a lot more astronomers now than there were in the 1800s.

In my Berkeley talk, I remarked that if things were to continue at the 5x faster rate, then 2011 should see the first discovery of a pair of planets in a Trojan configuration, echoing the discovery of the first Trojan asteroid, 588 Achilles, by Max Wolf of the Heidelberg Observatory in 1906.

Amazingly, it looks as if a pair of co-orbital “Trojan” planets has been found by Kepler. As detailed in the Lissauer, Ragozzine, Fabrycky et al. arXiv1102.0543 paper, The KOI 730 system contains transiting candidates with periods of 7.38, 9.84, 9.85, and 14.78 days — fully consistent with a 3:4:4:6 resonance:

The two middle planets (red and blue) in the configuration are participating in what are likely to be wide tadpole oscillations with respect to the equilateral equilibrium, like Hector chasing Patroclus around inside the Trojan Horse.

The above figures are adapted from a paper that John Chambers and I wrote in 2002 that explores the different flavors of one-to-one resonance that might exist among the extrasolar planets. I’m eager to sift the Kepler data to search for examples of the one-to-one “eccentric resonance” in which two planets share an orbital period and toss their orbital angular momentum back and forth like a hot potato:

It is mesmerizing to bring the KOI-730 candidates up in the systemic console, and watch the stability integration (try integrating for 500 years with an output frequency of 0.01 years). If one interprets the radial velocity wave-form as a audible signal, the system is simultaneously playing a fourth and an octave, with the longer-period libration distinctly heard as an unsteady vibrato.

A 10-second .WAV file (created with the Systemic Console) is here. This should play in your browser when the link is clicked.

It’s also interesting to note that the first clear picture of an asteroid was taken in 1992 by the Galileo probe, which passed close to 951 Gaspra on its way to Jupiter.

Pushing the five-fold increase in pace to its natural conclusion, means you should be sure to check this site in 2028…

Image Source.

The Kepler Candidates were just announced! My immediate sensation at seeing a copy of the associated paper is not unlike those cheesy contests where you’re allowed 60 seconds in a grocery store to grab whatever you can grab for free.

The most remarkable and unexpected development seems to be contained in Table 6 of the paper. Here, it looks as if candidates identified during the first four months of data collection have had their confidence levels increased through the use of additional transit measurements taken after September 16th, 2009. This allows for the identification of fifty candidate planets that might be considered prospects for potential “habitability”.

I ran the fifty planets in the table through my valuation formula (see here, and here.)

The total value of the planets in Kepler paper’s Table 6 is USD 295,897.65. As with most distributions of wealth, this one is highly inequitable — the most valuable planet candidate in the newly released crop is KOI 326.01, to which the formula assigns a value of USD 223,099.93. Assuming 5g/cc density, this planet has a mass of ~0.6 Earth masses, which is actually a little on the low side as far as the valuation formula is ensured. Nevertheless, USD 223,099.93 is a huge increase in value over Gl 581c, which charts at USD 158.32.

Back in 2009, I wrote that (in my opinion) the appropriate threshold for huge media excitement is USD 1M. With the planets in Table 6 of the paper, we are starting to get very close to that.

Here are the planets in the table with a formula valuation greater than one penny:

(These numbers are associated with a little bit of uncertainty. I’m using Kepler magnitudes rather than V magnitudes, and assuming 5 gm/cc. I’m also assuming that stellar mass goes as stellar radius. Running a cross correlation with the other tables in the paper will change the values slightly, but not substantially.)

The whole astronomical community is buzzing with anticipation over the imminent release of the unredacted First-Run Kepler results — all of the good stuff that was held back from the data release that occurred last June.

One can only imagine what might be contained — multiple-planet transiting systems, giant planet satellites, potentially habitable planets transiting low mass stars, a definitive answer to the super-Earth occurrence rate (to name but a few).

Once the candidates hit the stands, there will be a rush to skim the cream, and a mobilization of follow-up observational campaigns to capitalize on the best opportunities in the data set. With this eventuality in mind, Konstantin Batygin and I have prepared a follow-up characterization flow chart to aid fellow exoplanet prospectors in sifting potentially interesting systems — a template for the treasure map. As always, keep in mind that the brighter the individual parent star, the better the chances for the most interesting planetary characterizations.

Click here for a legible full-size version of the flowchart. (The paper containing it is focused primarily on the rather remarkable things one can do with tidally evolved multi-planet RV-detected systems. It’s been accepted to the Astrophysical Journal, and will appear on astro-ph shortly. It’s available now for download from oklo.org.)

NOAA Weather prediction is performed continuously by two IBM Power 575 Supercomputers named Stratus and Cirrus, each carrying out 69.7 trillion calculations per second. These machines each run 20 concurrent models for a global ensemble forecast. Approved production models run on Stratus, and development codes run on Cirrus. Huge volumes of this-just-in updates to the world’s atmospheric conditions pour in constantly from satellites, radiosondes, aircraft, ships and ground stations. The resulting predictions tend to be pretty good to about five days out:

Weather prediction would get a lot harder if the atmosphere was partially ionized. Not only would the ground stations melt, but the wind would no longer be able to blow freely through Earth’s magnetic field lines, which in turn would start to behave like rubber bands that resist being stretched and squeezed. The charged wind, furthermore, would experience Ohmic resistance that would create local heating.

On hot Jupiters, temperatures are high enough so that atmospheric alkali metals such as sodium and potassium are starting to ionize. This effectively guarantees that it’s necessary to do radiation magnetohydrodynamics in order to understand how these planets really work.

In a paper published last year, Konstantin Batygin and Dave Stevension showed that Ohmic dissipation is a very attractive mechanism for providing an extra energy source that inflates hot Jupiters and contributes to the bizarre range of radii exhibited by the transiting planets (radii that have caused a lot of consternation among those who tend to worry about such things).

Konstantin’s paper got me thinking about ways to test the Ohmic dissipation hypothesis. I wrote up some initial thoughts in this post from last summer. I’ve since worked things out further in collaboration with UCSC Physics Undergrad Matteo Crismani and with Fred Adams. We have a new paper on the topic that’ll be up on astro-ph later today.

We started with the data in the plot shown above, namely the disparate collection of transiting planets with well-measured masses and radii. We computed the radius anomaly for each of these planets, that is, the difference between a plain-vanilla structural model for a solar-composition planet with the observed mass and insolation and the actual observed radii.

These radius anomalies show a strong correlation with the amount of energy that they receive from their parent stars. If one examines power-law fits, it turns out that radius anomalies scale with temperature to the 1.4+/-0.6 power.

Our bottom line is that this power-law dependence is very much in line with what one might expect from Ohmic heating (if the back reaction of the magnetic field onto the wind speed is taken into account), and my guess is that Batygin and Stevenson have taken out a large chunk of the radius problem. (See also, their very recent follow-up paper with Peter Bodenheimer).

Our paper contains several pages of details that might not be appropriate for a family-oriented site such as oklo.org, so if you’re interested, then by all means download the .pdf and have a look…

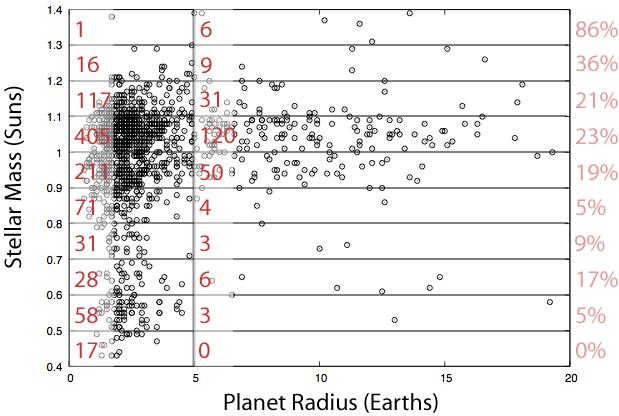
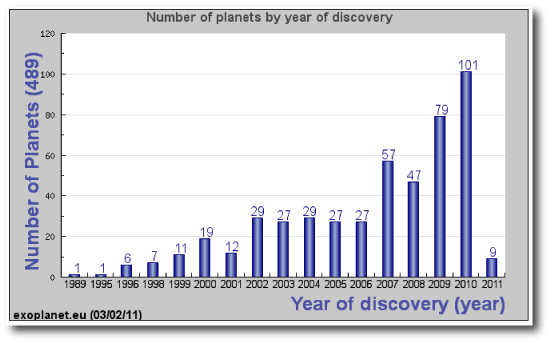
Here’s a selection of lead-off introductory lines from discovery papers of a completely random sample of planets announced in 2010:

With the discovery of extrasolar planets during the past 15 years, it has now become evident that our solar system is not unique. Similar to our Sun, many stars are believed to be hosts to giant and/or terrestrial-class planets and smaller objects.

In recent years, extending the threshold for exoplanet detection to yet lower and lower masses has been a significant endeavor for exoplanetary science. As at 2010 October, 31 exoplanets have been published with minimum (i.e., m sin(i)) masses of less than 20 Earth masses.

Radial velocity (RV) searches for extrasolar planets are discovering less massive planets by taking advantage of improved instrumental precision, higher observational cadence, and diagnostics to identify spurious signals. These discoveries include planets with minimum masses (M sin i) as low as 1.9 Earth masses (Mayor et al. 2009) and systems of multiple low-mass planets (Lovis et al. 2006; Fischer et al. 2008; Vogt et al. 2010). To date, 15 planets with M sin(i) < 10 Earth masses and 18 planets with M sin(i)=10–30 Earth masses have been discovered by the RV technique (Wright et al. 2010, Exoplanet Orbit Database10).

Ground-based transit surveys have been very successful at discovering short-period (P < 5 days) transiting extrasolar planets (TEPs) since 2006.

There has been a rapid increase in the number of transiting planets discovered each year due to dedicated ground– and space– based surveys: HAT (Bakos et al. 2002), TrES (Alonso et al. 2004), XO (McCullough et al. 2005),WASP (Pollacco et al. 2006), CoRoT (Baglin et al. 2006) and Kepler (Borucki et al. 2010). This trend looks set to continue, with the discovery of over 35 new planets published already this year (mid 2010), which represents more than a third of the total number of transiting planets known.

These soothing, robotic cadences are familiar to everyone who writes introductions and discussions for planet discovery papers. Those astronomers write prose with machine-like precision. Machine-like. Hmm…

Last year, after one of our “Wouldn’t it be cool if?” conversations, Stefano Meschiari decided to take up the daunting challenge of developing an NLG software package that can analyze radial velocity data, “discover” any statistically significant planets contained therein, and then write a publication-quality paper, that includes a human-readable introduction and analysis.

Stefano soon produced an amazing first-draft package, which he’s named “BAM” — short for Big Automatic Machine. Check out this screen-capture video of the systemic console hooked up to the BAM:

The Big Automatic Machine in action

There are certain advantages to having a computer write planet detection papers… BAM can go out on the Internet and scour the catalogs and the literature, which allows it to place new planets smoothly into the broader context. By looking at where new planets fall within the confines of all the known distributions, it can spot trends, peculiarities, and facets of interest.

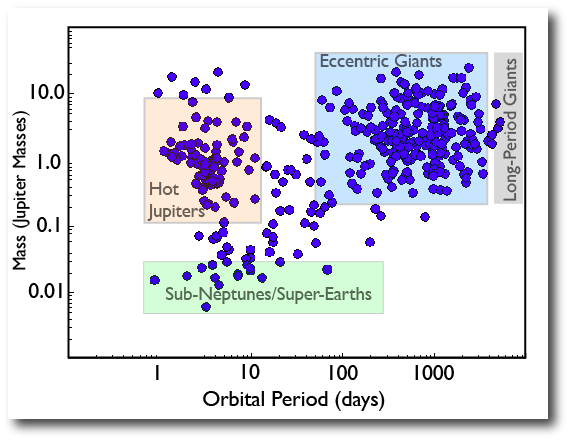
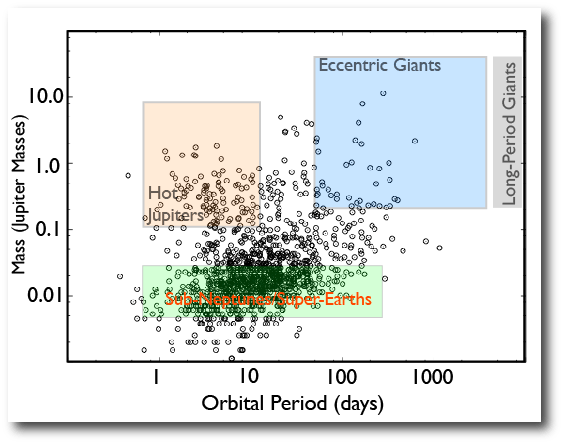
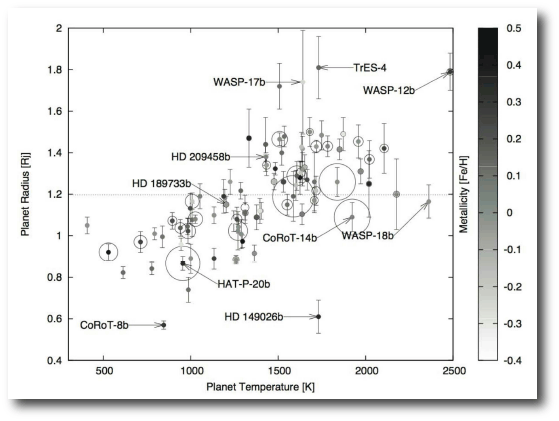
As an example, for the planets discussed in Stefano’s latest lead-authored paper, BAM notices that several of them fall in a somewhat sparsely populated region of the mass-period diagram:

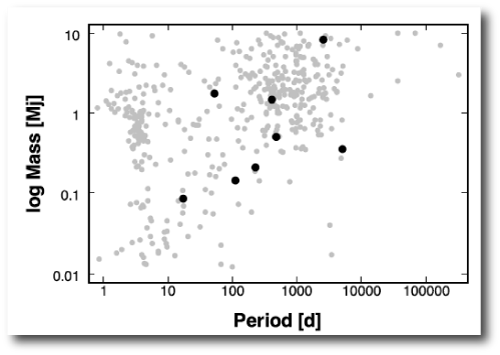
With a little coaxing and advice from its human minders, it now produces the following discussion:

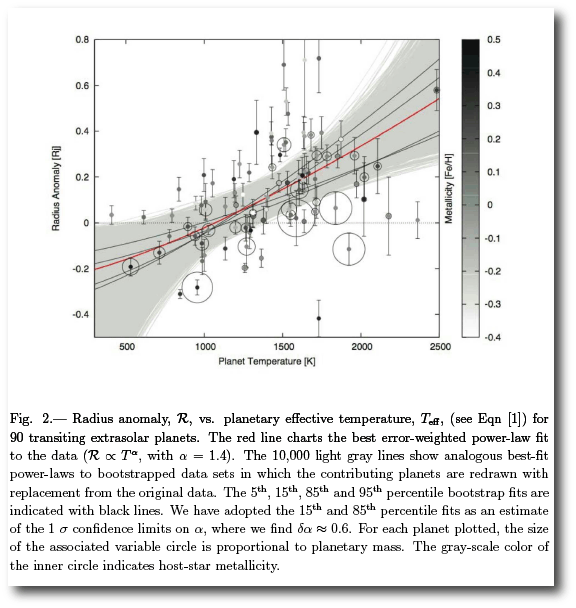
All the planets presented in this paper lie well within the existing exoplanet parameter envelopes (Fig. 15). Several of them lie in the so-called “desert” in the mass and semi-major axis distribution of extrasolar planets (Ida & Lin 2004). Monte-Carlo population synthesis models for extrasolar giant planet formation tend to suggest that planets migrate relatively rapidly through the period range between 10 and 100 days, and, in addition, often grow quickly through the mass range centered on the Saturnian mass. In the context of the overall planetary census, these four new planets help to further elucidate the various statistical properties of exoplanets. In particular, the discovery of multiple-planet systems helps in further characterizing the number of stars hosting multiple planetary companions and any correlations emerging in the distribution of orbital elements as suggested by observational clues (e.g. Wright et al. 2009).

With extrasolar planets as the topic, art retains a certain precedence over craft, and for the foreseeable future, BAM will be stuck with a learner’s permit — only allowed to drive if there’s a licensed driver in the car. I can imagine more mercenary, lawyerly, applications, however, where it will be able to really come into its own.

BAM, with its perfect command of LaTeX, its dry analytic mindset, and its cautiously factual discussions, writes prose that is pretty much the opposite of the writing that you’ll find in Jack Keroac’s On the Road. From the Wikipedia:

Keroac completed the first version of the novel during a three-week extended session of spontaneous confessional prose. Kerouac wrote the final draft in 20 days, with Joan, his wife, supplying him bowls of pea soup and mugs of coffee to keep him going. Before beginning, Kerouac cut sheets of tracing paper into long strips, wide enough for a type-writer, and taped them together into a 120-foot (37 m) long roll he then fed into the machine. This allowed him to type continuously without the interruption of reloading pages.

In the mid-1950’s, at the urging of Allen Ginsberg and William Burroughs, Keroac compiled a list of “essentials” for writing the spontaneous prose that comprises On the Road and his other work. Taken as a set of instructions, they seem almost perfectly designed to defy machine implementation in an NLG program. Take for example, the prescription for implementing proper structure:

STRUCTURE OF WORK
Modern bizarre structures (science fiction, etc.) arise from language being dead, “different” themes give illusion of “new” life. Follow roughly outlines in out fanning movement over subject, as river rock, so mind flowover jewel-center need (run your mind over it, once) arriving at pivot, where what was dim-formed “beginning” becomes sharp-necessitating “ending”and language shortens in race to wire of time-race of work, following laws of Deep Form, to conclusion, last words, last trickle-Night is The End.

One gets the feeling that the computers are still a decade or so away…

This coming July, the planet Neptune will have completed one full orbit since its discovery on September 23, 1846, an event which constituted the occasion, a week ago Sunday in Seattle, for a special session of the Historical Astronomy Division of the American Astronomical Society. From the conference program:

The year 2011 marks not only the 200th anniversary of the French mathematical astronomer Urbain Le Verrier’’s birth, but also the first return of Neptune to its optical-discovery position in 1846. Despite the passage of more than 164 years since that planet discovery, the circumstances surrounding the near-simultaneous mathematical predictions of a transuranian disturbing planet made by Le Verrier and John Couch Adams, a young Fellow in St. John’s College at the University of Cambridge, and the subsequent optical discovery of Neptune by German astronomer Johann Gottfried Galle at the Berlin Observatory continue to remain controversial. The double anniversary occurring in 2011 is an appropriate time to examine the Neptune discovery event from a number of new perspectives. In this session we shall explore how Cornwall shaped Adams’ early education and his method of locating the presence of a hypothetical disturbing planet. We shall examine the possibility that Adams (and perhaps Le Verrier as well) may have had Asperger’s Syndrome (high-functioning autism), a condition that may explain their difficulties in communicating and interacting with their contemporaries. The intense French press attack on British astronomers immediately after the discovery is examined in detail for the first time. The role that Benjamin Peirce’s analysis of Neptune’s actual orbit (which differed greatly from those hypothesized by Adams and Le Verrier) played in the development and European perception of American astronomy and mathematics will be discussed. We open and close the session with presentations placing the Neptune discovery event within the context of 19th-century science and relating it to modern-day searches for planets in the outskirts of the solar system and around other stars.

That Benjamin Peirce (pictured above), of the Harvard College Observatory, generally plays no role in the Astronomy 101 narrative of the discovery of Neptune is an interesting object lesson in itself: Nobody likes a playa hater. Peirce pointed out the inconvenient truth that the orbits calculated by Adams and LeVerrier, both of whom relied on Bodes’ law to inform their semi-major axes, are startlingly different from the actual orbit of Neptune:

In Peirce’s view, the discovery of Neptune constituted a “happy accident” because the event took place at the fortuitous time when the longitudes of the predicted and observed incarnations of Neptune lay near the same point on the ecliptic. Fast forward by one orbit, and the predictions don’t fare particularly well in a visual search with a 24.4 cm refractor:

Peirce did have a point. If you use a vague empirical law to inform a prediction, are you justified in reaping the accolades? Indeed, some of the praise that came to LeVerrier might justifiably have been seen as over-the-top:

I cannot attempt to convey… the impression that was made on me by the author’s undoubting confidence, but the firmness with which he proclaimed to the observing astronomers, `Look into the place which I have indicated and you will see the planet well.’

–George Bidell Airy, British Astronomer Royal

This scientist, this genius… had discovered a star with the tip of his pen, without other instrument that the strength of his calculations alone.

–Camille Flammarion

Now I’ll be the first to admit, I’m just about the last person who’s justified in taking the high road when it comes to planet “predictions”. For particularly egregious examples of my behavior in this particular regard, one need look no further than here, here or here. Nevertheless, here’s a set of obnoxiously rigorous criteria that I think would have satisfied even Benjamin Peirce’s exacting standards:

In order to be considered as having accurately “predicted” a planet, one must specify, prior to discovery, the planet’s

1. Mean anomaly to within +/- 19 degrees.
2. Argument of periastron to within +/- 19 degrees
3. Orbital eccentricity to within 0.1
4. Period to within 10%
5. Mass to within 10%
6. Inclination to within 10%
7. Longitude of the ascending node to within +/- 19 degrees.