A hundred, or even fifty-five years ago, it was thought that Mars and Venus might both harbor complex life, and the aspirations of science fiction writers and adventurers were pinned squarely on those two worlds. With the advent of space probes, however, we visited these planets, and the dream of lush sister worlds orbiting our own Sun was shattered. Mariner 2 reported the hot sulfurous truth about Venus; the crushingly poisonous atmosphere has no water and is hot enough to melt lead. Mars, when brought into focus by the Mariner and Viking probes, was only somewhat less disappointing. Aside from flood channels that have been bone-dry for billions of years, and the faint possibility that microbial life clings to the fringes of hypothesized hot springs, Mars has little to offer in the way of luxurious alien romance. For this, we must turn to other planets around other stars.

But we can still speculate. What would have happened if our solar system harbored a second, truly Earthlike, truly habitable world? What if there had been a genuine marquee destination for the cold war rockets?

Is such a planetary configuration dynamically feasible? We know that the continuously habitable zone around a star like the Sun may be relatively narrow. Is it possible to fit two Earth-mass planets within? More specifically, what would happen if we placed an exact copy of the Earth in the Earth’s orbit, with Earth’s orbital elements, and with the only difference being a 180 degree advance in the mean anomaly. In other words, what would the dynamical consequences be if Earth had a twin on the other side of the Sun?

In 1906, the German astronomer Maximillian Franz Joseph Cornelius Wolf discovered an asteroid at roughly Jupiter’s distance from the Sun which was orbiting roughly 60 degrees ahead of Jupiter, and thus forming a point of an Equilateral triangle with Jupiter and the Sun. It was soon realized that the orbit of this asteroid was very stable, since it is positioned at the so-called Jovian L4 point, one of the five stable Lagrangian points associated with the Sun and Jupiter. These points represent special solutions to the notorious three-body problem, and were discovered in 1772 by the Italian-French mathematician Joseph Louis Lagrange. The following diagram was lifted from the wikipedia:

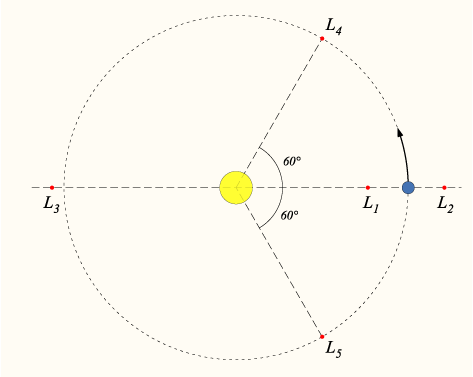
Wolf named his Jupiter-L4 asteroid 588 Achilles, after the sulky Greek hero of Homer’s Illiad. A year later, August Kopff discovered a similar asteroid, this one orbiting at the so-called L5 point, 60 degrees behind Jupiter. In keeping with the Homeric tradition launched by Wolf, Kopff named his asteroid 617 Patroclus, after Achilles’ gentleman friend and fellow greek warrior. Thus, with fitting cosmic symmetry, the two heroes were immortalized in the heavens to either side of mighty Jupiter.

Later in 1907, Kopff discovered a third co-orbital asteroid of Jupiter, this one near L4, which he named 624 Hektor, in honor of Achilles’ Trojan nemesis. Hubble Space Telescope observations indicate that Hektor is actually a contact binary,
in which two asteroids are effectively glued together by their weak gravity. In 1908, Wolf discovered yet another object (659 Nestor) near Jupiter’s L4 point. It was clear that a whole class of Trojan asteroids existed, and in order to keep things straight, it was decided that asteroids found near L4 would be named after Greeks (the Greek camp), whereas asteroids near L5 would be named after Trojans (the Trojan camp). Hektor and Patrocles, who were thus orbiting in the camps of their respective enemies, were given the unique status of spies.
Nearly two thousand trojan asteroids are now known. Even minor figures such as Hektor’s infant son (1871 Astyanax) are now attached to asteroids, and the Illiad’s roster is nearly completely exhausted. Trojan asteroids of recent province, such as 84709 2002 VW120 are relegated to the status of neutral observers.

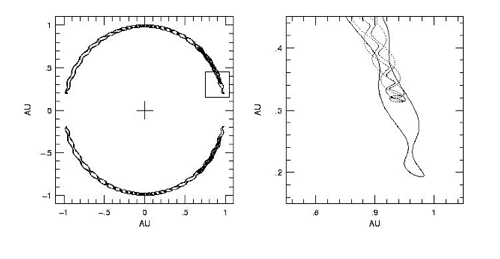
The US Navy maintains a website that charts the orbital motion of a number of trojan asteroids. (The Navy’s involvement seems rather appropriate, as it was Helen, whose beauty was sufficient to launch a thousand ships, who touched off the Trojan War.) As a Trojan asteroid orbits the Sun, it also orbits about its Lagrange point by executing two essentially independent librations. The combination of the two librational motions leads to an intricate motion when viewed in a frame that rotates along with Jupiter.

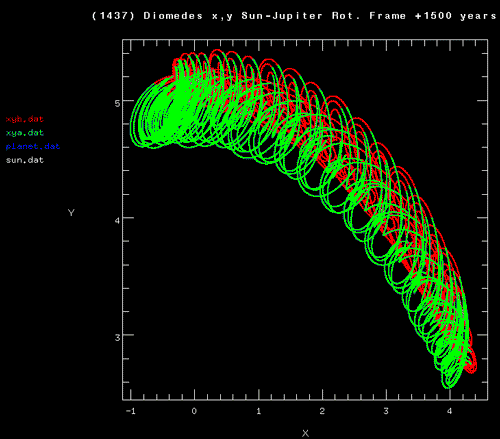
Back to our hypothetical Doppelganger of the Earth.

In the language of Lagrange, when we place a new world on the opposite side of the Sun from the Earth, we have populated the L3 point. A linear perturbation analysis shows that if an object at L3 is perturbed, then the orbit will drift steadily away from the initial L3 location. That is, the orbit is linearly unstable, in contrast to the the orbits at L4 and L5, which are linearly stable, and hence stick around in the vicinity of trojan points, even when they are subjected to orbital perturbations.

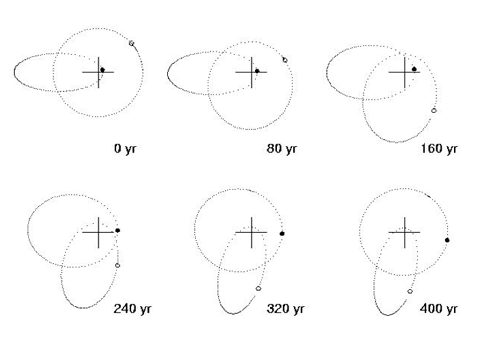
A computer is required to find out what would happen to the orbits of the Earth and our hypothetical twin planet. It turns out that the motion is nonlinearly stable. The Earth and its twin would be perfectly content, and, in a frame rotating with a 365 day period, the motion of the two planets over a period of years would look like this:

As one planet tries to pass the other one up, it receives a forward gravitational pull. This forward pull gives the planet energy, which causes it to move to a larger-radius orbit, which causes its orbital period to increase, which causes it to begin to lag behind. Likewise, the planet which is about to be passed up receives a backward gravitational pull. This backward pull drains energy from the orbit, causes the semi-major axis to decrease, and causes the period to get shorter. The two planets are thus able to toss a bit of their joint orbital energy back and forth like a hot potato, and orbit in a perfectly stable variety of a 1:1 orbital resonance, known as a horseshoe configuration. The horseshoe orbit is an example of the negative heat capacity of self-gravitating systems, which is one of the most important concepts in astrophysics: If you try to drain heat away from a self gravitating object, it gets hotter.

Here’s a thought. It is dynamically possible that 51 Peg b (or any of the other extrasolar planets that do not transit within the predicted window) is actually two planets participating in a stable 1:1 orbital resonance…

While we’re on the topic of far-out planetary configurations, another type of allowed 1:1 configuration is the 1:1 eccentric resonance, an example of which is shown below. In this situation, two Jupiter-mass planets share the same period, but have very different eccentricities.

Over time, the planets pass their eccentricity back and forth in an endless resonant cycle. If one of these configurations is found orbiting a sun-like star, it will induce a very distinctive radial velocity curve which will allow an unambiguous determination of the planetary masses and inclinations. And you can rest assured that the code that generates the systemic database is fully aware of the different flavors of one-to-one resonance.

This post isn’t yet complete, so check back later if it has caught your interest…