“The past year has given to us the new [minor] planet Astraea; it has done more – it has given us the probable prospect of another. We see it as Columbus saw America from the far shores of Spain. Its movements have been felt, trembling along the far-reaching line of our analysis with a certainty hardly inferior to ocular demonstration.”

— Sir John Herschel addressing the British Association of the Advancement of Science on Sept. 15, 1846, two weeks prior to the discovery of Neptune.

Yesterday, Ryan Montgomery gave his presentation at the AbSciCon meeting in Washington DC, and laid forth our provocative hypothesis. We think that Earth-mass planets are common in the habitable zones of the lowest-mass red dwarf stars, and we think that these planets can potentially be detected by targeted photometric searches of the nearest known low-mass stars. The closest stars on this list are accessible to transitsearch.org observers, and we are advocating that the search begin immediately.

Our calculations use John Chambers’ Mercury integrator to follow the last evolutionary stages of a planetesimal swarm in the protoplanetary disk of a young low-mass red dwarf star. The underlying physical picture in the simulations is that the star and disk are of order one million years old. The initial stages of planet formation are assumed to already have been completed. Grains of solid material have stuck together to build larger and larger objects in the disk. Most of the gas that was originally in the disk has either accreted onto the star, or has been photoevaporated by high-energy photons from the star itself and the neighboring stars in the birth aggregate.

We’ve completed three sets of calculations, and our computers are currently working on a large number of additional runs. In the first set (containing sixty individual simulations) we assume that two Neptune-like giant planet cores have already managed to form beyond the protostellar ice line, where the temperature is lower than 150K, and where planets can grow more quickly because of the availability of ices. We also assume that the innermost Neptune-mass core has been able to migrate a small ways inward to a distance of ~0.2 AU from the central star. This situation was chosen so as to be in analogy with the known Neptune-mass planets orbiting the red dwarfs GL 436 and GL 581 (see yesterday’s post). In a second set of sixty simulations, we didn’t include the giant planet cores. In our simulations, the Neptune-mass cores assume a role similar to that which Jupiter and Saturn are believed to have had during the formation phases of the terrestrial planets in our own solar system.

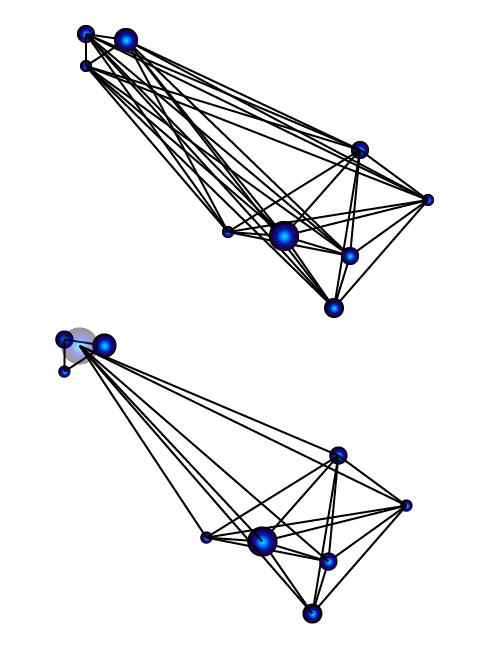
In each of the 120 simulations that comprise the first two sets, we distribute 1000 planetesimals in initially circular orbits in the region between 0.04 AU and 0.12 AU surrounding the eventual stellar habitable zone for the 0.12 solar mass star. Each planetesimal contains 0.003 Earth masses (about a quarter of a lunar mass). The swarm of planetesimals is then allowed to evolve under its own self-gravity, the gravity of the star, and the gravity of the ice-giant cores (if they are present). Planetesimals that collide with each other are assumed to conserve total angular momentum in the collision, while merging into a larger composite body. Some planetesimals collide with the ice giants or with the star, or are thrown out of the system. In a typical simulation (shown below) the swarm rapidly works itself down over a period of a few thousand years into a system of several terrestrial mass planets. Earth-mass planets in the habitable zone of the star are a very common outcome of the simulations.

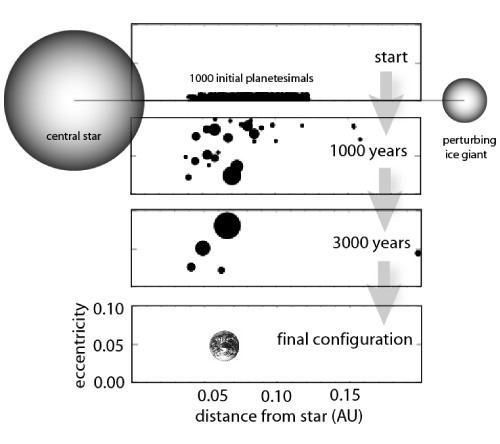
In a third set (of thirty) simulations, we lowered the masses of the planetesimals to 0.0003 Earth-masses, that is, a factor of ten times lower. The results of these simulations were the formation of Mars-sized or smaller bodies in the stellar habitable zone.

The results have a simple interpretation. The final stages of terrestrial planet formation in the protoplanetary disks of red dwarf stars appears to be an efficient process. If one starts with an adequately high effective surface density of solid material in the disk, then one frequently gets Earth-mass planets in the habitable zone. If one starts with a lower surface density, then one gets final sets of terrestrial planets that (on average) have proportionally lower masses, i.e., no deal.

We believe that the key issue, then, is: what is the appropriate surface density to use?

If one makes reasonable extrapolations from the minimum-mass solar nebula that formed our own solar system, or if one extrapolates from the dust disks which are observed around young stars in the solar neighborhood (see the photo below of the disk orbiting AU Microscopium), then one should adopt a low surface density. This was the approach taken by Sean Raymond in his talk (which followed Ryan at AbSciCon). Sean’s results agreed quite well with our low-surface density simulations, namely, Mars-sized or smaller planets in the habitable zones of red dwarfs.

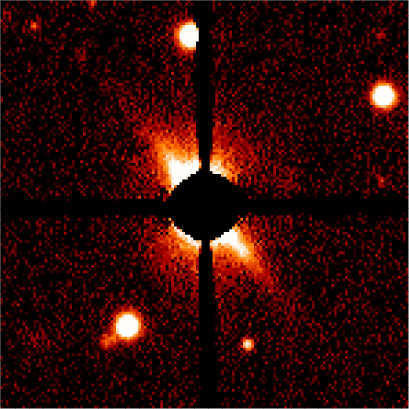
Submillimeter observations of dust masses in young stellar systems measure the amount of mass in dust, and are not directly sensitive to the amount of mass in large, planetesimal-sized bodies. Furthermore, such measurements give the dust mass at large distances (say greater than 1 astronomical unit at least) from the star, and hence do not give information about the mass of solids present in the innermost region of the disk.

Our preferred high surface density scenario is based on the “Minimum Mass Nebulae” for the inner regions of GJ 876 (0.32 solar mass), and Jupiter (0.001 solar mass). These are the two objects closest in mass to our hypothetical 0.12 solar mass star whose “terrestrial planet” systems we can measure.

In the case of Jupiter, the moon Io has a mass of 8.93e+25 grams, an orbital radius of 0.0028 AU, and an orbital period of 1.8 days. This implies a solid surface density of approximately 12,000 grams per square centimeter at the 1.8 day orbital radius in the proto-Jovian nebula.

In the case of GJ 876, planet “d” (which you can characterize from the actual Keck and Lick radial velocity data using the Systemic Console) has a mass of 4.5e+28 grams (7.5 Earth masses), an orbital radius of 0.02 AU, and an orbital period of 1.94 days. If we assume that GJ 876 d fed off material reaching out to a radius of 0.075 AU, then this implies a solid surface density of 11,000 grams per square centimeter at the 2.0 day orbital radius in GJ 876’s protoplanetary nebula. This is remarkably close to the value for Io. That is, the “rule of thumb” from these two systems suggests an effective surface density of solid material of ~10,000 grams per square centimeter at a 2-day orbital period.

The similarity between the solid surface densities obtained by grinding up Io and GJ 876d suggests that we also adopt a solid surface density of 11,000 grams per square centimeter at the 2-day orbital radius for our 0.12 solar mass star (0.015 AU). Using a reasonable r^-3/2 falloff in surface density as we move away from the star, this suggests a fiducial density of 2000 grams per square centimeter at a habitable-zone radius of 0.045 AU, which is the value that we use in our preferred (sets 1 and 2) simulations.

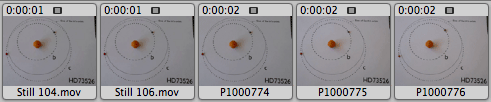
Once we’ve run a particular simulation, we choose a random angle from which the system is to be viewed. We then generate photometry that is typical of what high-end amateur observers such as Ron Bissinger or Tonny Vanmunster are capable of regularly achieving. For instance, here’s an example of Ron Bissinger’s observation of HD 149026b shortly after it was discovered.

We then “observe” the system by creating a simulated photometric time-series over a period of several hours, during the intervals in which a transit might possibly occur.

Our simulations imply about a 1.0% a-priori probability that a 0.12 solar mass red dwarf has a detectable, habitable planet. That means that most of the simulated systems, when observed at a random viewing angle, don’t show any transits:

With the omnipotence afforded by the simulation output files, we know that some of the simulations were not that far away from having a transiting planet:

Whereas some were closer still:

In this case, a tiny planet produces a grazing transit that is completely unobservable with 0.4% differential photometry:

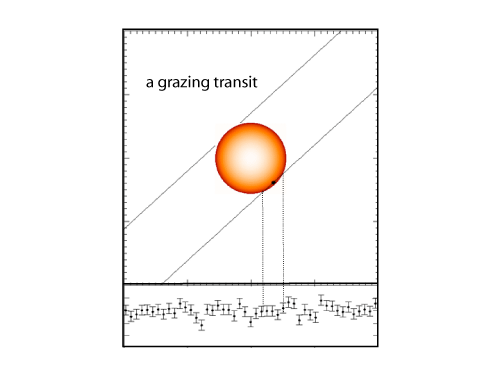
And then, finally, gloriously:

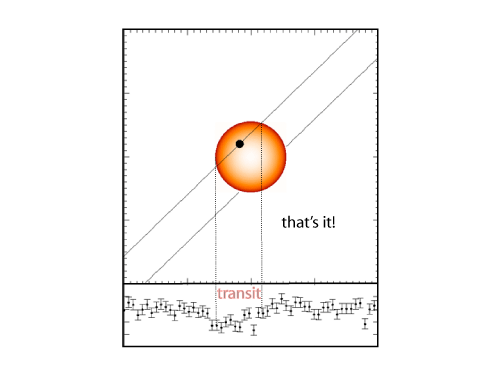
That’s how I think we’ll get our first look at a truly habitable world orbiting an alien star.

Finally, back to the passage from John Herschel that starts this post off with an egregious bang. At first glance, it looks like a totally outrageous bit of self-serving grandstanding. Moreover, the quote itself is well-known to the extent that a reasonable person might justifiably press charges of second or even first degree cliche. On second glance, however, it actually seems rather appropriate.

Columbus thought he was headed for the East Indies, and he was justifying his expedition on an assumed distance from the Canary Islands to Japan of only 4444 km (as opposed to the true distance of 19,600 km). He had no conception whatever of America while he was still on the “far shores of Spain.”

Furthermore, the prediction of the existence of Neptune by Urbain Jean Joseph LeVerrier, was based on the large perturbations to the orbit of Uranus which occured from ~1810-1840, and which only occur once per Uranus-Neptune conjunction. The large derangement of Uranus’ orbit allowed LeVerrier to compute predicted ephemerides for the location of Neptune that were accurate enough for it to be quickly discovered by Johann Galle and Heinrich d’Arrest on the night of Sept. 23, 1846. LeVerrier was lucky, however. Even though he assumed an incorrect distance for Neptune of 36.15 AU, based on Bode’s spurious “law”, his method — which was essentially a laborious hand-cranked version of what goes on beneath the hood of the Systemic Console — was able to compensate for this incorrect assumption by invoking a mass for Neptune that was too large (2.9 times too large, in fact), and an eccentricity, e=0.11, that was also too large. Neptune’s actual orbit is currently nearly circular, with e=0.00884. As a result, LeVerrier’s orbital predictions of the location of Neptune in the skies of 1846 were close enough to allow it to be found, even though his predicted planet had an orbital period of 217 years, in comparison to Neptune’s actual period of only 166 years.

This point is often glossed over in the astronomical lore, and LeVerrier (with Adams invariably in tow) is lionized a bit too assiduously as a hero of the scientific method. In fact, luck, in the form of the fact that Uranus and Neptune happened to be close to conjunction, played a major, if not leading role. At the end of the day, we expect the same situation to hold true for those habitable planets transiting nearby low-mass red dwarf stars.

The Solar System was once a gigantic black cloud in space, imbued with a tiny overall spin in some particular random direction. The net spin of our ancient protostellar cloud is still manifest in today’s solar system. The planets all orbit the Sun in a direction counterclockwise as seen from above. The major planetary satellites (with the exception of Triton) all orbit counterclockwise as well. The Sun spins on an axis that lies within 7 degrees of the average orbital plane of the planet.

The law of conservation of momentum suggests that alien planetary systems should display a similar state of orbital affairs. When a planetary system forms more or less quiescently, and more or less in isolation, then the final spin axis of the parent star should be nearly perpendicular to the orbital plane of the planets.

If the stellar equator and the planetary orbital planes are far from alignment, then we have evidence that disruptive events occurred early in the history of the planetary system. Spin-orbit misalignment hints at planetary collisions, ejections, and other dramatic events. In the Solar System, for example, the crazy 97.77 degree tilt of Uranus’ polar axis may be evidence that a large (perhaps Earth-mass) object collided with Uranus early in its history, leaving its spin axis askew, and its poles bathed in an endless succession 42-year days.

In a new paper accepted for publication in the Astrophysical Journal, members of the systemic team have participated in an investigation of the spin-orbit alignment of the recently discovered transiting planet orbiting HD149026. Our goal was to get a better sense of whether this star-planet system suffered a catastrophe in its distant past.

HD 149026 b was discovered last year by N2K (the discovery paper is here). The planet has a mass ~114 times that of the Earth (slightly bigger than Saturn) and has a 2.875 day orbital period. By measuring how the star’s light dims as the planet passes in front of the star, it’s possible to determine the size and the exact orbital geometry for the system. Here’s a scale model in which the star, and the planet, and the orbit are all shown in their correct proportions:

Perhaps the most charming aspect of HD 149026 b (to the limited extent that a scalding 1600K planet can exert charm) is that the planetary sidereal year lasts exactly one weekend. That is, if you punch a clock at noon on Friday, the planet has made one full orbit at 9:01 am the following Monday.

Perhaps the most scientifically interesting aspect of HD 149026 b is its small size. The transit depth is only 0.3%, which implies that the planet has a radius of only ~0.7 Jupiter radii. That is surprisingly small, given the high temperature on the planetary surface, and tells us that the planet is quite dense. It needs to contain at least 50 Earth masses of elements heavier than hydrogen and helium. This huge burden of heavy elements is hard to explain. One possibility is that the planet was built up from the collision of several Uranus or Neptune like objects. If this were the case, then one might expect that the final orbital plane could be significantly misaligned with the equatorial plane of the star.

Our measurement of the spin-orbit alignment for HD 149026 makes use of a phenomenon known as the Rossiter-McLaughlin effect. In 1924, Rossiter and McLaughlin independently measured the spin-orbit alignment of the eclipsing binary systems beta-Lyrae and Algol by modeling the variations in the measured radial velocities of the stars during transit. This effect, now appropriately called the Rossiter-McLaughlin effect, occurs any time an object (star or planet) occults part of a rotating stellar surface. The following figure shows how a rotating star outputs a small red-blue shifted version of its spectrum as we examine the changing radial spin-velocity from one limb to the other. When a planet passes in front of the oncoming limb, it blocks out red-shifted light, while the planet blocks out blue-shifted light when covering the outgoing limb. This is interpreted by the radial velocity code as a positive and then negative shift in the radial velocity of the star. The amplitude of this effect is thus due both to the spin velocity of the star as well as the total flux blocked out during transit.

The Rossiter effect can be used to tell us how closely the stellar equator is aligned to with the orbital plane of the planet. When the planet’s path across the stellar disk is not parallel to the stellar equator, the radial velocity zero-point does not occur at the transit mid-point, and the radial velocity curve is asymmetric. The figure above illustrates how this works.

High-cadence radial velocity observations taken during a transit are required to accurately measure the Rossiter effect. The in-transit velocities can be combined with other data, including the out-of-transit radial velocities which constrain the planetary orbit, and the transit photometry. An overall coupled model of all of these data can then give us the best possible picture of the system. Our new paper describes the exact details of how such an overall model can be constructed for HD 149026. The end result is that the equator of the star and the orbital plane of the transiting planet are quite well aligned; we measure the value of the misalignment angle to be 11 plus or minus 14 degrees.

Although a fourteen degree (1-sigma) uncertainty is more than we’d like, it nevertheless provides an excellent constraint on the HD 149026 system. Since the misalignment of our own sun is ~7 degrees relative to the net planetary orbital angular momentum, and because we believe that the solar system formed fairly quiescently, we are primarily interested in whether HD 149026 b sports a severe misalignment (say 40 degrees or more). From our modelling, it’s clear that the orbit and planetary spin are not egregiously out of whack. Hence, there’s no evidence of a particularly disruptive formation history. That is, no catastrophic orbit altering collisions between massive protostellar cores. Rather, we are left with evidence of a more traditional, more mundane history, in which planetary formation was dominated by gradual accretion and the prolonged interactions with a planetary disk

And the mystery of HD 149026b’s large core persists. How did all those heavy elements — all that oxygen, nitrogen, carbon, iron, gold, get into the planet?

Our favored explanation draws on a scenario described by Frank Shu in 1995, in which the planetesimal migrates radially inward through the planetary disk until it reaches the interior 2:1 resonance with the “magnetic X-point,” the outermost point at which closed stellar magnetic field lines intersected the planetary disk. At the X-point, heated ionized gas is forced to leave the disk and climb up the field lines to accrete directly onto the star. In this occurs, the planetismal is stuck in a gas-starved environment for the remainder of the disk lifetime, and is essentially fed nothing but rocks and heavy elements for millions of years. The end result is a crazy-large 72 Earth-mass core in the middle of a 114 Earth-mass planet.

A very interesting new planetary system has been discovered in orbit around the nearby star HD 73526, a solar-type main sequence dwarf visible from the Southern Hemisphere. The discovery was made by Chris Tinney, Paul Butler, Geoff Marcy and their collaborators on the Anglo Australian Planet Search Project. The discovery paper has been accepted by the Astrophysical Journal, and a preprint describing the discovery has been posted to arXiv.org.

[Photo of persimmons at Rakushisha, Kyoto, Japan, c2005 Adriane Steinacker]

The system contains two giant planets. The inner, slightly more massive planet (imaginatively named “b”) contains at least 3 Jupiter masses, and orbits with a 188 day period. The outer planet, c, is only slightly less massive, with about 2.5 Jupiter masses. It orbits with a period of roughly 379 days. Planet c is a true room temperature gas giant. Liquid water likely blows in gusty sheets across its cloudy skies. (And it’s worth noting that any large moons circling HD 73526 c lie pleasantly within the stellar habitable zone.)

The large masses of the two planets, and their relatively small orbital separation, indicate that they exert strong perturbations on each other’s motion. It appears that in order for the system to be stable, it is required that b and c exist in a protective 2:1 resonance. In other words, on average, planet c circles the parent star exactly half as many times as does planet b. Amazingly, however, it appears that the periastron points of the two orbits are not locked in sync, but rather circulate at very different rates around the star. This situation leads to a bizarre orbital motion when plotted over thousands of years. I’ve made an mpeg animation which shows how this works. In the animation, the clockhand like lines show the periastron angles of the orbits. They undergo a crazy, almost drunken, dance, but somehow, the system configuration manages to remain stable indefinitely.

I’ve also added the published radial velocity data for HD 73526 to the Systemic Console. Take a peek at the published orbital parameters (both Keplerian and dynamical) if you have a hard time rolling the Console’s Levenberg-Marquardt algorithm into the best-fit configuration. I will put up a post shortly which goes into more detail about the dynamics of this fascinating system and what they tell us about planetary formation.

This post follows up post #14, The Next Big Thing.

In 1916, in circular #30 of South Africa’s Union Observatory , Robert T. A. Innes reported the discovery of a faint red star in Centaurus. This otherwise unremarkable star, more than 100 times too faint to be seen with the naked eye, attracted his attention because it was rapidly moving with respect to other stars in the same part of the sky. This large proper motion indicated that the star was almost certainly a close neighbor of the Sun, and in 1917, this suggestion was verified. The distance to the star was measured to be only 4.22 light years, closer to the Sun than any other known star. Its extremely faint appearance, in spite of its close proximity, made it the intrinsically least luminous star known to astronomy at that time.

Proxima Centauri, as the star was later named, is now known to be merely the nearest (and most famous) of the roughly 50 billion red dwarfs (also called M-dwarfs) which inhabit our galaxy.

What about planets? Is it possible to have a terrestrial planet in orbit around Proxima? Do red dwarfs have a shot at harboring life-bearing worlds? If such worlds exist can we detect them?

Yes.

Continue reading →