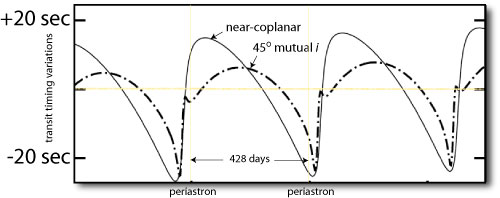
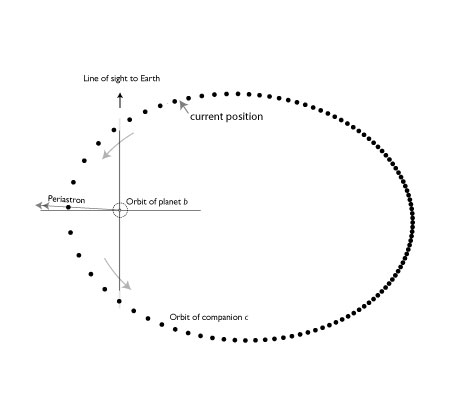
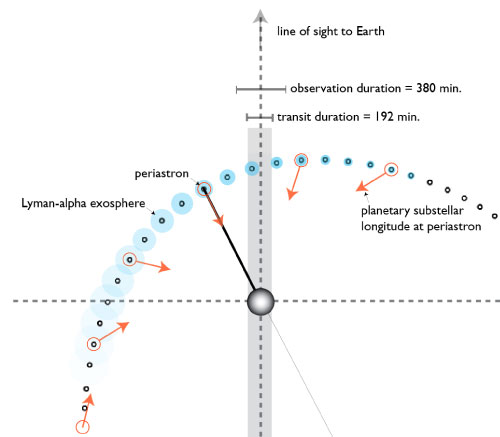
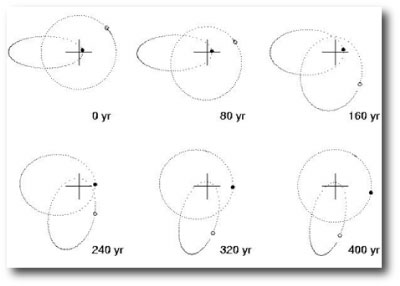
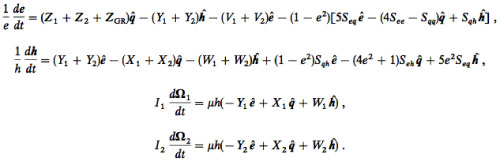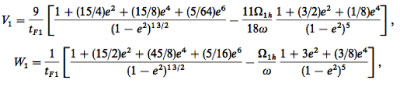Transit timing variations have a certain allure. Most extrasolar planets are found by patiently visiting and revisiting a star, and the glamour has begun to drain from this enterprise. Inferring, on the other hand, the presence of an unknown body — a “Planet X” — from its subtle deranging influences on the orbit of another, already known, planet is a more cooly cerebral endeavor. Yet to date, the TTV technique has not achieved its promise. The planet census accumulates exclusively via tried and true methods. 455 ± 21 at last count.

Backing a planet out of the perturbations that it induces is an example of an inverse problem. The detection of Neptune in 1846 remains the classic example. In that now increasingly distant age where new planets were headline news, the successful solution of an inverse problem was a secure route to scientific (and material) fame. The first TTV-detected planet won’t generate a chaired position for its discoverer, but it will most certainly be a feather in a cap.

Where inverse problems are concerned, being lucky can be of equal or greater importance than being right. Both Adams’ and Le Verrier’s masses and semi-major axes for Neptune were badly off (Grant 1852). What counted, however, was the fact that they had Neptune’s September 1846 sky position almost exactly right. LeVerrier pinpointed Neptune to an angular distance of only 55 arc-minutes from its true position, that is, to the correct 1/15,600th patch of the entire sky

In the past five years, a literature has been growing in anticipation of the detection of transit timing variations. The first two important papers — this one by Eric Agol and collaborators, and this one by Matt Holman and Norm Murray — came out nearly simultaneously in 2005, and showed that the detection of TTVs will be eminently feasible when the right systems turn up. More recently, a series of articles led by David Nesvorny (here, here, and here) take a direct stab at outlining solution methods for the TTV inverse problem, and illustrate that the degeneracy of solutions, the fly in the ointment for pinpointing Neptune’s orbit, will also be a severe problem when it comes to pinning down the perturbers of transiting planets from transit timing variations alone.

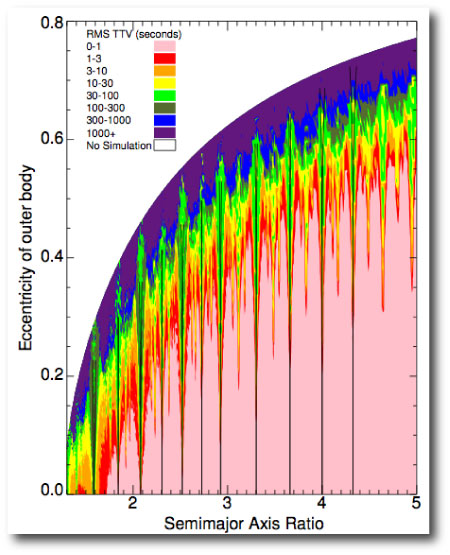
In general, transit timing variations are much stronger and much easier to detect if the unseen perturbing body is in mean-motion resonance with the known transiting planet. In a paper recently submitted to the Astrophysical Journal, Dimitri Veras, Eric Ford and Matthew Payne have carried out a thorough survey of exactly what one can expect for different transiter-perturber configurations, with a focus on systems where the transiting planet is a standard-issue hot Jupiter and the exterior perturber has the mass of the Earth. They show that for systems lying near integer period ratios, tiny changes in the system initial conditions can have huge effects on the amplitude of the resulting TTVs. Here’s one of the key figures from their paper — a map of median TTVs arising from perturbing Earths with various orbital periods and eccentricities:

The crazy-colored detail — which Veras et al. describe as the “flames of resonance” — gives the quite accurate impression that definitive solutions to the TTV inverse problem will not be easy to achieve. One of the conclusions drawn by the Veras et al. paper is that even in favorable cases, one needs to have at least fifty well-measured transits if the perturber is to tracked down via timing measurements alone.

The Kepler Mission holds out the promise of systems in which TTVs will be simultaneously present, well measured, and abundant. In anticipation of real TTV data, Stefano Meschiari has worked hard to update the Systemic Console so that it can be used to get practical solutions to the inverse problem defined by a joint TTV-RV data set. An improved console that can solve the problem is available for download, and a paper describing the method is now on astro-ph. In short, the technique of simulated annealing seems to provide the best route to finding solutions.

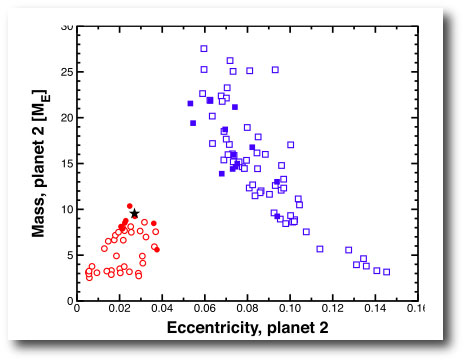
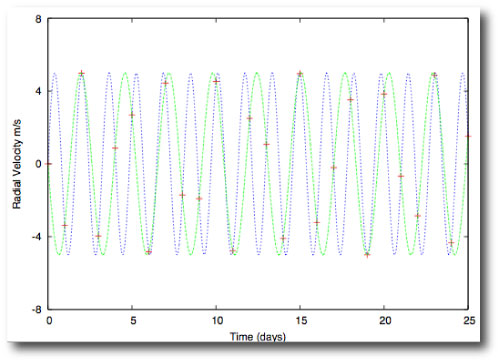
A data set with TTVs alone makes for a purer inverse problem, but it looks like it’s going to be generally impractical to characterize a perturber on the basis of photometric data alone. Consider an example from our paper. We generated a fiducial TTV system by migrating a relatively hefty 10 Earth-mass planet deep into 2:1 resonance with a planet assumed to be a twin to HAT-P-7. We then created data sets spanning a full year, and consisting of 166 consecutive measurements, each having 17-second precision, and a relatively modest set of radial velocity measurements. We launched a number of simulated annealing experiments and allowed the parameters of the perturbing planet to float freely.

The resulting solutions to the synthetic data set cluster around configurations where the perturber is in 2:1 resonance (red symbols), and solutions where it is in 3:1 resonance (blue symbols). Furthermore, increasing the precision of the transit timing measurements to 4.3 seconds per transit (solid symbols) does little to break the degeneracy:

The upshot of our paper is that high-quality RV measurements will integral to full characterizations of the planets that generate TTVs. At risk of sounding like a broken record, this means that to extract genuine value, one needs the brightest available stars for transits…

It’d be rather unsettling to sit down with a cup of coffee one morning, and learn from astro-ph that the orbital period of Mars is not 1.88 years as is widely believed, but is rather a mere 7.83 months.

Last week, Rebekah Dawson and Dan Fabrycky posted a paper that gave me an equivalent jolt, and which has likely touched off a certain uproar within the planet-hunting community. Their claim is that the periods of a number of A-list planets, including 55 Cnc e and HD 156668 b are in fact aliases, and that the true periods of these worlds are startlingly different. Dawson and Fabrycky argue that the true period of 55 Cnc e is a fleet 0.7365 days (revised from 2.817d), and that HD 156668b orbits with a period of 1.2699 days rather than the published value of 4.6455d. Other well-known worlds may well be in line for a similar treatment.

Sometimes, things seem very clear in retrospect. In the graph just below, I’ve plotted the reflex velocity curves for two planets. One has a period of 1.61803 days, the other has a a period of 2.61803 days. If one happens to observe only at the times when the curves intersect, then it’s clear that there’s no way to tell them apart.

In the particular case above, the intersections of the sinusoids are separated by exactly one day. If the true period of the system is 1.61803 days, then we would say that the 2.61803 day period is an alias produced by the 1-day observing frequency. In general, for an observing frequency, f_o, and a true period, f_t, aliases exist at frequencies f=f_t+m*f_o, where m is an integer.

Aliases are a problem in Doppler surveys because observations are most efficiently done when the star is crossing the meridian, leading to a natural spacing of one sidereal day (23h 56m) between data points. Further periodicities in data-taking arise because RV survey time is usually granted during “bright” time when the Moon is up, and as a consequence of the yearly observing season for non-circumpolar stars. Aliases are minimized when observations are taken randomly, but the nuts and bolts of the celestial cycles impose regularity on the timestamps.

In reducing the period of 55 Cnc e to a sizzling 17.7 hours, the probability that the planet transits is raised to a very respectable 25%. Seems to me like rolling the dice with a few hours of Warm Spitzer time might be in order.

Controversy generates revenue for exoplanet weblogs and supermarket tabloids alike, so I’m always happy when planet-related press releases roll out dramatic, far-reaching claims. Last week’s ESO press release — “Turning Planetary Theory Upside Down” — was quite satisfactory in this regard…

Upon digging into the back story, one finds that the observations underlying the press release are fully uncontroversial — it’s the big-picture interpretation that’s turning heads. Using Doppler velocity measurements taken during transit, Triaud et al. (preprint here) have measured the sky-projected misalignment angles, λ, for six of the transiting planets discovered by the SuperWASP consortium.

After an initial run of nine transiting planets were found to have sky-projected misalignment angles close to zero, the current count now has 8 out of 26 planets sporting significant misalignment. In the standard paradigm where hot Jupiters form beyond the ice line and migrate inward to reach weekend-length orbits, one would expect that essentially all transiting planets should be more or less aligned with the equators of their parent stars.

The standard migration paradigm, however, leaves at least two questions rather vaguely answered. First, why do the hot Jupiters tend to halt their inward migration just at the brink of disaster? The distribution of orbital periods — slew of selection biases aside — shows a durable peak near ~3 days. Second, why are transiting planets with well-characterized companions so scarce? In general, if one finds a giant planet with a period of ~10 days or more, the odds are excellent that there are further planets to be found in the system. For the known aggregate of transiting planets, and for hot Jupiters in general, additional planets with periods of a few hundred days or less are only infrequently found.

HD 80606b provides a clue that processes other than disk migration might be generating the observed population of hot Jupiters. The planet HD 80606b, its parent star HD 80606, and the binary companion HD 80607 form a “hierarchical triple” system, in which the two large stars provide an unchanging Keplerian orbit that drives the orbital and spin evolution of HD 80606b. If we imagine that HD 80606b and HD 80606 are both subject to small amounts of tidal dissipation, then to plausible approximation, this paper by Eggleton & Kiseleva-Eggleton argues that (i) the orbital evolution of “b”, (ii) the spin vector of “b”, and (iii) the spin vector of HD 80606 itself  can be described by a set of coupled first-order ordinary differential equations:

where e and h are vectors describing the planetary orbit, and where Ω_1 and Ω_2 are the spin vectors for HD 80606 and HD 80606b. The equations are somewhat more complicated than they appear at first glance, with expressions such as:

making up the various terms on the right hand sides.

Numerical integrations of the ODEs indicate that solutions exist in which the e and h vectors for `606b are bouncing like a ’64 Impala. Check out, for example, this solution vector animation by Dan Fabrycky (using initial conditions published by Wu and Murray 2003) which shows the leading scenario for how HD 80606b came to occupy its present state.

HD 80606b is imagined to have originally formed in a relatively circular orbit that was roughly 5 AU from its parent star, and which happened to be at nearly a right angle to the plane of the HD 80606-HD80607 binary orbit:

The large mutual inclination led to Kozai oscillations in which ‘606b was cyclically driven to very high eccentricity. During the high-eccentricity phases, tidal dissipation within the planet gradually drained energy from the orbit and decreased the semi-major axis:

Eventually, the orbital period became short enough so that general relativistic precession was fast enough to destroy the Kozai oscillations, and the planet was marooned on a high-eccentricity, gradually circularizing orbit that is severely misaligned with the stellar equator — exactly what is observed:

With HD 80606b, the case for Kozai-migration is pretty clear cut. The guilty party — the perturbing binary companion — is sitting right there in the field of view, and the scenario provides an easy explanation for anomalously high orbital orbital eccentricity. The only “just-so” provision is the requirement that the planet-forming protoplanetary disk of HD 80606 started out essentially perpendicular to the orbital plane of its wide binary companion.

The Triaud et al paper and the press release draw the much more dramatic conclusion that Kozai cycles with tidal friction could be the dominant channel for producing of the known hot Jupiters. From the abstract of their paper:

Conclusions. Most hot Jupiters are misaligned, with a large variety of spin-orbit angles. We observe that the histogram of projected obliquities matches closely the theoretical distributions of using Kozai cycles and tidal friction. If these observational facts are confirmed in the future, we may then conclude that most hot Jupiters are formed by this very mechanism without the need to use type I or II migration. At present, type I or II migration alone cannot explain the observations.

Can this really be the case? Might it be time to start reigning in the funding for studies of Type II migration in protostellar disks?

A key point to keep in mind is that Rossiter-McLaughlin measurements yield the sky-projected misalignment angle, λ, between the stellar spin and planetary orbital angular momentum vectors, and not the true misalignment angle, ψ, in three-dimensional space. That is, with transit spectroscopy alone, you can’t discern the difference between the following configurations:

In a paper published in 2007, Dan Fabrycky carried out integrations of the Eggleton-Kiseleva-Eggleton equations for an ensemble of a thousand star-planet-star systems that experience HD80606-style Kozai migration coupled with tidal friction. From the results of the integrations, he constructed a histogram showing the distribution of final misalignment angles, ψ:

The first nine Rossiter-McLaughlin observations of transiting planets all produced values for λ that were close to zero, in seeming conflict with Fabrycky’s distribution for ψ. The jump-the-gun conclusion, then, was that Kozai-migration is not an important formation channel for hot Jupiters.

With the spin-orbit determinations that appear in the Triaud et al. paper, there are now a total of 26 λ determinations. A fair fraction of the recent results indicate severely misaligned systems, and Triaud et al. show a histogram over λ (or in their notation, β):

In order to compare the observed distribution of λ measurements with Fabrycky’s predicted distribtion of Kozai-migration misalignments, ψ, Triaud et al. assume that the distribution of spin axes for the transit-bearing stars is isotropic. With this assumption, one can statistically deproject the λ distribution and recast it as a &#968 distribution, giving a startlingly good match between Fabrycky’s theory (blue dashed line) and observation:

When I first saw the above plot, I had a hard time believing it. The assumption that the spin axes of transit-bearing stars are isotropically distributed seems somewhat akin to baking a result into the data. Nevertheless, it is true that if Kozai migration produces the hot Jupiters, then the current ψ distribution is right in line with expectations.

In early 2009, Fabrycky and Winn did a very careful analysis of the 11 Rossiter measurements that were known at that time. Among those first 11 measurements, only XO-3 displayed a significant sky-projected spin-orbit misalignment. From the sparse data set, Fabrycky and Winn concluded that there were likely 2 separate populations of transit-bearing stars. One population, in which the spins and orbits are all aligned, constitutes (1-f)>64% of systems, whereas a second population, sporting random alignments, is responsible for f<36% of systems (to 95% confidence).

Bottom line conclusion? More Rossiter-McLaughlin measurements are needed, but I think its safe to say that Kozai-migration plays a larger role in sculpting the planet distribution than previously believed. If I had to put down money, I’d bet f=50%.

Competition keeps everyone on their toes, and the exoplanet Doppler detection game is no exception.

The California Planet Search has recently done a major overhaul of their exoplanets.org website, and the results are impressive. The redesigned site is now fully interactive, and it must be seeing a lot of traffic. Certainly, I can count myself as a frequent visitor!

Perhaps the most exciting feature of the site is a plotting applet that seamlessly connects to an up-to-date and curated database of the known extrasolar planets. In the “advanced” mode, one can get very finely tuned plots that can tell interesting stories. As an example, here is a plot of RV half-amplitudes of the known planets plotted against the RMS of the residuals to the fits. The color of the points corresponds to discovery year (cool = back in the day) and the size of each point corresponds to the number of published RV data points for the planet (those five big points correspond to 55 Cancri b-f which has a very extensive data set).

The plot shows that progress comes in part from competition. As the competing Doppler surveys push to lower Ks, there has a been a trend toward decreased signal-to-noise for the detections. It looks like oklo.org posts a few years from now will likely be discussing systems with K~60 cm/sec. At that amplitude, one is plausibly talking habitable worlds.

Another interesting plot comes from plotting parent star metallicity against planet mass. As with most of the interesting diagrams, a logarithmic scaling is required. The parent star masses are keyed to the sizes of the individual points, and color is assigned to eccentricity. The software has the nice feature that a cursor placed on a dot informs you of the planet name. This plot shows the benefit of looking at lower mass stars, and it shows how the metallicity correlation is diminished as one pushes below roughly a Saturn mass (evidence, of course, for core accretion):

The exoplanets.org site also contains a very useful planet table, which is giving the competition (in this case, exoplanet.eu) a run for its money.

The question of how the world’s top Doppler teams match up in league play is something that I imagine comes up quite a bit in exoplanet-related water-cooler discussions. A suitable scoring system is therefore in order, and the tables on exoplanets.org make this a very doable proposition.

After some thought, I’ve decided to adopt the system used for cross-country running, with the K‘s of the team’s planets replacing the times of the team’s runners. (The image for this post is from a 1983 dual meet between two high school teams from Central Illinois. If you look carefully, you can see that the coach is hurling an acorn at yours truly, presumably because of the much wider-than-expected gap between runners #2 and #3.) In the exoplanet context, the cross-country scoring system encourages fluid changes of lead — one or two high-grade multiple super-Earth systems can catapult a team to the top of the board. From the wikipedia article:

When two or more teams of cross country runners compete, a score may be compiled to determine which team is the better. Points are awarded to the individual runners of eligible teams, equal to the position in which they cross the finish line (first place gets 1 point, second place gets 2 points, etc). Teams are considered ineligible to score if they have fewer than the meet’s required number of scorers, which is typically five. Only the first five runners in for a team are counted towards that team’s score; the points for these runners are summed, and the teams are ranked based on the total, with lowest being best. In the event of a tie, the rules vary depending on the competition; often the team that closes scoring first wins, though in the US NCAA ties are possible. In high school competition, if two teams tie, then the victor is decided by whose sixth runner, the first one whose score does not count, finished first.

The lowest possible score in a five-to-score match is 15 (1+2+3+4+5), achieved by a team’s runners finishing in each of the top five positions. If there is a single opposing team then they would have a score of 40 (6+7+8+9+10), which can be considered a “sweep” for the winning team. In some competitions a team’s sixth and seventh runner are scored in the overall field and are known as “pushers” or “displacers” as their place can count ahead of other runners. In the above match, if there are two non-scoring runners and they came 6th and 7th overall, the opponent’s score would be 50 (8+9+10+11+12). Accordingly, the official score of a forfeited dual meet is 15-50.

According to the above rules, there are currently three RV teams in the running. The Geneva Extrasolar Planet Search (whose planets I’ve listed with SWISS on the table), the California Planet Search (planets listed with CPS), and the Earthbound Planet Search (who I’ve marked as EPS):

The score as of this morning? SWISS 25, EPS 47, CPS 62…

So when presented with that particular formulation, I generally prefer to get the bad news first:

Stefano Meschiari and I have investigated how the new radial velocity data for the HAT-P-13 system affect the possibility of measuring transit timing variations for the short-period planet “b” as the heavy, long-period planet “c” rumbles through its periastron passage later this spring.

First, recall the overall set-up. HAT-P-13 was discovered in transit by Gaspar Bakos and his HAT Net collaborators last summer. HAT-P-13 “b” is a standard-issue hot Jupiter with 0.85 Jupiter masses and a fleeting 2.916-day orbital period. The radial velocity follow-up indicated that the system also contains an Msin(i)~14.5 Jupiter mass object on an eccentric orbit with a P~430 day period. If the two planets are close to coplanar, then the system should have tidally evolved to an eccentricity fixed point — a configuration that allows one to extract Juno-mission style interior information from the inner planet for free.

System Version 1.0 for HAT-P-13 generates significant transit timing variations for the inner planet during the weeks surrounding the periastron passage of the outer planet. In a post two weeks ago, I showed some invigorating calculations by Matthew Payne and Eric Ford, which charted the details of the timing variations. Here’s a figure inspired by the Payne-Ford analysis that uses the systemic console’s TTV routines to zoom in on the imminent HAT-P-13 periastron:

The above picture is quite rosy, at least as far as the outlook for TTVs is concerned. With orbital models that are based on the Bakos et al. discovery data for the system, the transit-to-transit time intervals for planet b veer from ~17 seconds shorter than average to ~17 seconds longer than average (relative to the long-term mean) as planet c runs through its periastron and exerts its maximum perturbing influence. This shift from a compressed period to an expanded period occurs rather abruptly over a span of about 2 weeks. Most provocatively, there are significant and feasibly observable differences between the TTV profiles produced by the coplanar configuration and by the configurations with 45-degree mutual inclinations. And finally, all the action was predicted to occur just before the end of HAT-P-13’s yearly observing season (see Bruce Gary’s revived AXA page for wealth of additional detail). It’s not hard to revel in the thought of all the ground-based observers pooling their results (in the spirit of 1761 and 1769) and emerging with a big-picture result!

The new Winn et al. data, however, definitely rain on the TTV parade. The augmented (out-of-transit) data set now shows that the period of planet c is about 20 days longer than previously believed, and c’s eccentricity also drops slightly, from e_c=0.69 to e_c=0.666. With the new orbital model, the differences in the TTVs generated by the co-planar and mutually inclined configurations are considerably smaller. The overall amplitude of the variations is cut nearly in half, and the excitement is pushed far more precariously against the end of the observing season:

And the good news? As described in the last post, the Winn et al. data show that the orbital plane of planet b is probably aligned with the equator of the parent star, which, in turn, means that it’s quite likely that the b-c system is indeed coplanar.

If we assume coplanarity, then the system should be at an eccentricity fixed point in which the apsides of the two planets are aligned. A measurement of the eccentricity of planet b then allows the interior structure and the tidal dissipation of planet b to be measured.

The augmented radial velocity data set permits a better measurement of planet b’s orbital eccentricity. Figure 5 of the Winn et al. paper has the relevant plot, which shows the distribution of Markov-Chain models for the eccentricity and apsidal angle of planet b. If the orbits are aligned, then the true model needs to fall within the red dotted lines, which mark the position of the (much better determined) apsidal line for planet c. From looking at the figure, the apsidally aligned configurations seem to have e_b ~ 0.01±0.005.

I asked Josh if he could send a histogram that shows the distribution of eccentricities for planet b for the subset of models that satisfy the alignment criterion. He got back to me very quickly with the following plot:

The result is: e_b = 0.0106 ± 0.0040, which implies a best-guess planetary structure that has (1) a small core, (2) a Love number k_2~0.34, and (3) a tidal dissipation quality factor Q~10,000 (see our paper, Batygin, Bodenheimer & Laughlin 2009 for details).

HAT-P-13c could easily wind up being 2010’s version of HD 80606b — a long-shot transit candidate that pans out to enable extraordinary follow-up characterization, while simultaneously allowing small-telescope ground-based observers to stunt on the transit-hunting space missions.

The HAT-P-13 system has already gotten quite a bit of oklo.org press (see articles [1], [2], and [3]). It generates intense interest because it’s the only known configuration where a transiting short-period planet is accompanied by a long-period companion planet on an orbit that’s reasonably well characterized by radial velocity measurements. Right after the system was discovered, we showed that if the orbits of the two planets are coplanar, then one can probe the interior structure of the transiting inner planet by getting a precise measurement of its orbital eccentricity. The idea is that the system has tidally evolved to an eccentricity fixed point, in which the apsidal lines of the two planets precess at the same rate. Both the precession rate and the inner planet’s eccentricity are single-valued functions of the degree of mass concentration within the transiting planet.

Early this year, Rosemary Mardling expanded the analysis to the situation where the two planets are not orbiting in the same plane (her paper here). If there is significant non-coplanarity, the system will have settled into a limit cycle, in which the eccentricity of the inner planet and the alignment angle of the apsidal lines cycle through a smoothly varying sequence of values. The existence of a limit cycle screws up the possibility of making a precise statement about planet’s b’s interior, even if one has an accurate measurement of the eccentricity.

When one ties all the lines of argument together, it turns out that there are two different system configurations that satisfy all the current constraints. In one, the planetary trajectories are nearly co-planar, with the inclination angle between the two orbits being less than 10 degrees. If the system has this set-up, then we’ll be in good position to x-ray the inner planet. In the alternative configuration, the orbital planes have a relative inclination of ~45 degrees, and the limit cycle will hold.

Matthew Payne, a postdoc at Florida, along with Eric Ford, have done a detailed examination of the transit timing variations that the two configurations will produce. (Transit timing variations — or TTV as all the hipsters were referring to them last week at SXSW — have been all the rage during the last few years, but have so far generated more buzz than results. That should change when HAT-P-13 takes the stage.) Payne and Ford found that timing variations should amount to tens of seconds near the periastron of planet c, which should in turn allow a resolution of whether the system is co-planar or not:

HAT-P-13 is a tough system for small-telescope observers to reach milli-magnitude precision at a cadence high enough to accurately measure the transit timing variations. Nevertheless, the top backyard aces will be giving it a go. Bruce Gary has reactivated the AXA especially for the event, and University of Florida grad student Ben Nelson has written a campaign page for Lubos Brat’s Tresca database. The best transits for detecting TTV will be occurring during April and May. This is an opportunity to really push the envelope.

If the system turns out to be close to coplanar, then there’s a non-negligible probability (of order 5-10%) that planet c will be observable in transit. The transit window is centered on April 12th, and is uncertain by a few days to either side. Small telescope observers will definitely be competitive in checking for the transit. In an upcoming post, we’ll take a look at the details and the peculiarities of this remarkable opportunity.

It’s been rather arduous past few days as the HST Cycle-18 proposal deadline — 5 PM PST, Friday Feb. 26th, to be exact — bore down like a freight train.

During the past year, I’ve become quite intrigued by the remarkable (and well known) HST observation by Vidal Madjar et al. (2003), who discovered that the Lyman-alpha transit depth of HD 209458b is a whopping 15% (as opposed to the mere 1.5% of the star’s light that gets blocked during the optical transit). The implication of this result is that the planet is surrounded by an outflowing, escaping wind of hydrogen, and the discovery has sparked a lot of theoretical work.

A good test for planetary outflow hypotheses is to see what they predict for eccentric planets that undergo drastic changes in stellar heating during the course of the orbit. Fred Adams and I have been working on hydrodynamical models for these situations, and it soon became clear that oklo.org fave HD 17156b, the P=21.2d, e=0.67 transiting planet provides an intriguing observational opportunity for HST/STIS. HD 17156 is currently the fourth-brightest known parent star of a transiting extrasolar planet (after HD 209458, HD 189733 and HD 149026) and it lies in HST’s so-called continuous viewing zone for part of the year. This means that a full transit can be observed without having to take those leisurely once-per-96-minute pit stops every time Earth blocks the view.

The geometry of the transit, furthermore, is such that the planet is getting its maximum sunburn just a few hours after transit egress. Our calculations indicate that it should take the upper atmosphere only a matter of hours to react to the increased heating, so we’re optimistic about the possibility that not only will HST detect a deep transit in the UV, but that it might even be able to detect the Lyman-alpha transit depth increasing during the course of the transit. Here’s the basic idea:

As of a few minutes ago, the proposal was received safe and sound at STScI, so now it’s time to kick back, wait, and see if it passes muster with the TAC…

I’ve got an upcoming event planned in New York City that should be pretty interesting. From the UCSC Newsletter:

UCSC astronomer joins composer Philip Glass to explore music of the universe

UC Santa Cruz Astronomer Gregory Laughlin joins acclaimed composer Philip Glass February 21 in a “Brainwave” discussion at the Rubin Art Museum in New York.

For its third year and in conjunction with the exhibition Visions of the Cosmos, Brainwave is a series of 20 sessions this winter and spring that bring together eminent thinkers from multiple disciplines with neuroscientists and astrophysicists to ponder big thoughts about “things that matter.”

Laughlin and Glass appear in the third Brainwave event titled “How Do We Listen to the Music of the Spheres?”

Laughlin is a professor of astronomy and astrophysics whose research delves into orbital dynamics and the evolution of planetary systems. Glass is one of the most influential composers of the past half-century. Though sometimes called a “minimalist,” Glass describes his compositions as “music with repetitive structures.”

Laughlin said he and Glass will explore commonalities between music and orbital dynamics. The museum’s initiative to pair the two was sparked in part by Laughlin’s articles on his blog oklo.org that delve into ways to “sonify” planetary movements.

He developed software to map planetary systems as audible waveforms. He said he became intrigued by the realization that planetary systems can be used as a type of nonlinear digital synthesizer and can provide an enormous palette of sound — sounds never before heard.

The Laughlin/Glass Brainwave session begins at 6 p.m. Sunday, February 21 at the Rubin Museum of Art at 150 West 17 St., New York City. Admission is $25.

Over the next week, as I’m preparing for the event, I’ll be working extensively with the sonification capability of the systemic console. Just below, is a reprinted post that touches on this very cool, and still relatively unexplored feature. If you’ve worked with the Console’s N-body sonification, and if you’ve found interesting results, feel free to send me .fit files — an extraordinarily effective form of compression(!) — and I may be able to use them in the discussion.

Potentially the most interesting feature on the downloadable systemic console is the “sonify button”, which integrates the model planetary system specified by the state of the console sliders and produces a .wav format CD-quality audio file of the resulting radial velocity waveform. Not interested in planets? The console is a stand-alone non-linear digital synthesizer. It’s capable of producing strange, remarkable, musically useful sounds. They merely need to be located within the uncountable infinity of solutions to the gravitational N-body problem.

First, use the console to build an interesting multi-planet system (for this purpose, there’s no need to try to fit whatever data is in the window.) Then click the sonify button. This brings up a dialogue window which enables the user to make several specifications for the sound file that is produced.

The most important user-specified parameter is the frequency onto which the orbital period of the shortest-period planet on the console is mapped. If, for example, the innermost planet has a period of 365.25 days, then a 440 Hz map will play 440 years worth of evolution in one second. (440 Hz corresponds to the A below middle C.) Mapping the radial velocity curve onto a high-frequency note extends the total number of orbits that go into the sample, and thus increases the integration time required to produce the sample. You can also specify the length of the sample, and you can exert simple control over the attack and decay rate of the envelope for the overall waveform.

Once you’ve produced the sound file, it appears in the “soundClips” subdirectory within the systemic parent directory. Both of these directories are automatically created when you download and expand the console — see the instruction set for the downloadable console for more details. With a Macintosh, you get the best results if you play the sample right from the folder. i-Tunes seems to want to convert the samples to .mp3 format in a manner that introduces audible noise, and we’re not yet sure how to resolve this issue.

To the extent that planets orbit independently of one another, the console behaves like a simple additive synthesizer, in which the individual Kepler waveforms add to form a composite sound. Much more interesting, is the situation when planets experience significant gravitational interaction, leading, for example, to resonance and to nonlinear instability (here are examples, 1, 2, from the resources page of both types of waveforms). Close encounters provide discontinuities between individual blocks of sound that resemble the results of granular synthesis.

The strongest 2-planet mean-motion resonances occur when the pair of planets share a common period and engage in a one-to-one resonant motion. There are a variety of different one-to-one resonances, including binary planet orbits (e.g. Earth and Moon), trojan configurations, and generalizations of retrograde satellite orbits. In this last category, one can have two planets with the same semi-major axis, but with different eccentricities. If one starts the planets in the following configuration, then the motion is dynamically stable, and evolves in a complicated way over time.

The motion leads to an interesting audio wave-form, in which you can hear the system cycling between configurations in which both planets are modestly eccentric and configurations in which one orbit is nearly circular while the other one is highly eccentric. As a specific example, set the console to the following configuration: P1=P2=10 days, M1=M2=0.3 Mjup, MA1=180., MA2=190., e1=0.9, e2=0.1, long1=0.0, long2=0.0. If you increase MA2 to about 225 degrees while keeping the other parameters fixed, you’ll hear the system go unstable.

Evolving, high-eccentricity orbits tend to have an insect-like quality, which brings to mind the 1986 album, The Insect Musicians, by Greame Revell (formerly of SPK). From the album jacket:

For the two years 1984-85, Graeme Revell traveled from Australia to Europe, to Africa, Indonesia and North America recording and negotiating copyrights of insect sound recordings. It took another full year sampling and metamorphosing some forty sounds thus gathered using the Fairlight Computer Musical Instrument, to produce this record. The only sounds used are those of insects, altered digitally and combined into a unique orchestra of instruments, an orchestra of strange and delicate timbres, music of natural rhythm and texture.