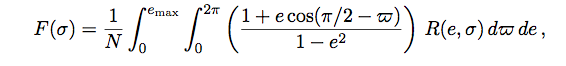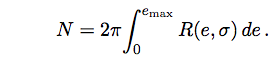The French philosopher of science Isidore Auguste Marie François Xavier Comte (1798 – 1857) was the founder of sociology and is widely remembered for the doctrine of positivism, which holds that the scientific method can be used to understand both natural and social phenomena.

He’s well known to astronomers, however, largely because of the spectacularly incorrect statements regarding stars in his Cours de la Philosophie Positive (1830-1842):

On the subject of stars, all investigations which are not ultimately reducible to simple visual observations are … necessarily denied to us. While we can conceive of the possibility of determining their shapes, their sizes, and their motions, we shall never be able by any means to study their chemical composition or their mineralogical structure … Our knowledge concerning their gaseous envelopes is necessarily limited to their existence, size … and refractive power, we shall not at all be able to determine their chemical composition or even their density… I regard any notion concerning the true mean temperature of the various stars as forever denied to us.

Lots of fun to get your introductory lecture on stellar spectroscopy off to a snarky start with that particular zinger.

Comte’s pronouncements on planets are slightly more obscure, but now, given the many and varied successes of the Spitzer Telescope, they provide an equally rich vein for irony-with-20/20-hindsight:

The take away message seems to be “never say never”. Nowadays, an academic with Comte’s flair would certainly have the innate sense to leave some wriggle room in anticipation of unforeseen scientific advances.

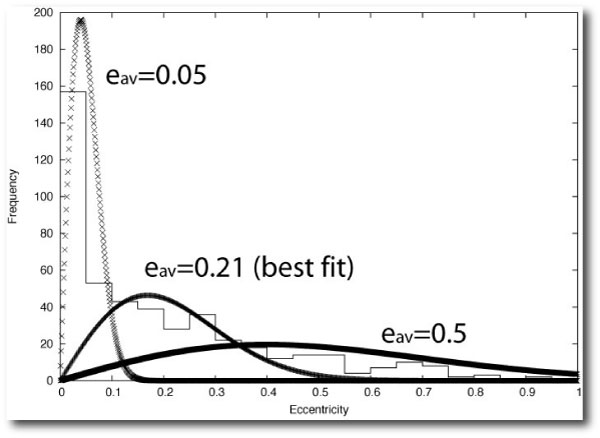
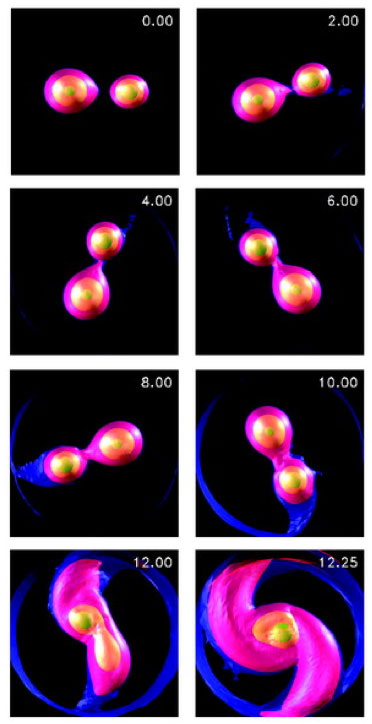
In any case, in this evening’s astro-ph mailing, there’s a very interesting article by Brugamyer et al. that touches on the inferred chemical and mineralogical structure of extrasolar planets. The authors of the paper make a detailed examination of the relative oxygen and silicon abundances of stars known to host extrasolar planets.

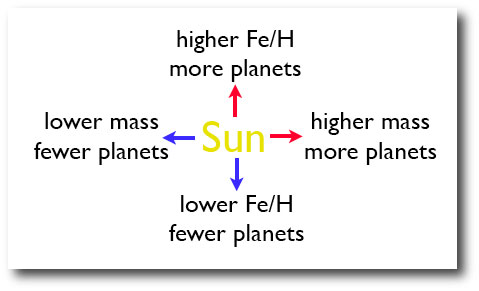
The context comes from work back in 2006 by co-author Sally Dodson-Robinson which indicated that stars with high silicon abundances relative to iron show increased planet fractions at given metallicity:

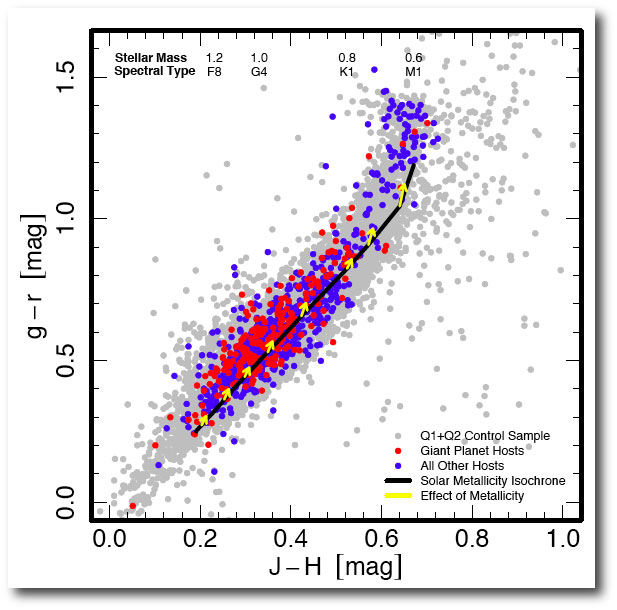
The expectation was that stars with high oxygen abundances relative to iron would also show increased planet fractions at given overall metallicity. Oxygen is a key component of the core-building materials for giant planets, and so it stood to reason that the more water available, the more Jupiter-mass planets one ends up with. Remarkably, this turns out not to be true. Here’s the relevant diagram from the Brugamyer et al paper:

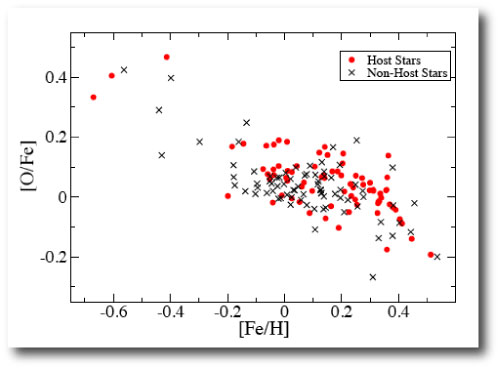
Statistically, it appears that an excess of oxygen relative to iron has no influence on the likelihood of a given star hosting a readily detectable planet. The silicon effect, however, is statistically robust and readily detectable in the Brugamyer et al. analysis:

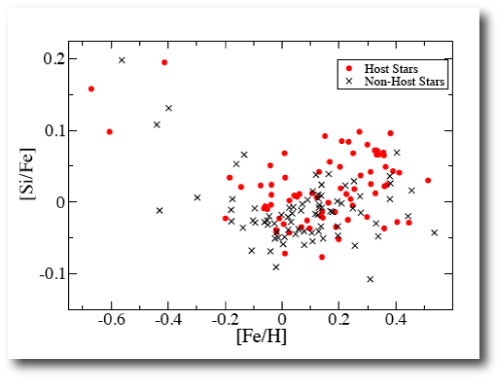
So how does one explain the unexpected result? Brugamyer et al.’s hypothesis is that icy grain nucleation on silicon-rich dust, rather than the subsequent growth of the icy core-forming particles, is the key bottleneck in forming giant planets via core accretion.

An all-time classic of the literature is Alar and Juri Toomre’s 1972 ApJ study of colliding galaxies. With an exceptionally simple physical model — the restricted three body approximation, in which test particles orbit in the joint potential provided by two massive bodies on a conic 2-body trajectory — the Toomre brothers were able to construct startlingly plausible explanations for bizarrely irregular galaxies such as the Antennae.

One is hard-pressed to think of a better example of seeing the essence of a manifestly complicated phenomenon so precisely nailed by a simple model. The take-away lesson seems to be: Keep an eye out for situations in which glorious non-linearity has had of order one Lyapunov time to unfold.

ApJ 178, 623 also presents some of the finest astronomical diagrams ever. They are masterpieces of visual scientific communication. Every single detail conveys information, and nothing is superfluous.

In 1998, when I was a post-doc in Berkeley, my working routine was considerably less hectic than it is now. On the foggy morning of May 29th of that year, I remember buying a copy of the New York Times, and settling in at a Cafe on Telegraph Avenue for a relaxed 11AM coffee. A picture and a slew of familiar names jumped off the front page:

The story, which became a huge media event — even President Clinton made a passing mention of it — stirred up a uniquely unsettled, uniquely urgent feeling of being completely involved and completely left out all at the same time. A runaway planet clearly would have formed via gravitational instability, and I had spent several years studying gravitational instabilities for my PhD thesis. I gulped down my coffee, scooped up the paper and ran to my office in Campbell Hall. The phone was ringing when I got there. Doug Lin was on the line, buzzing with excitement. “It’s a tidal tail! Look at Alar’s ’72 paper!”

There was not a moment to waste… Doug called the editor at Science and informed him that we had an important interpretive result in the works. I stayed up all night putting together SPH simulations. It seemed completely feasible that one could explain the observation with a collision between two protostellar disks, in which the runaway planet formed via gravitational collapse in the tidal tail. We got the paper off to Science in short order, and boy was it exhilarating!

The Toomre brothers’ influence soaks right through the figures that I made for our paper. Thirteen years on, they remind me of listening to a cover of Sympathy for the Devil done by a competent Stones tribute band.

Sadly, a year or so later, it became clear that the TMR-1c runaway “planet” is, in actual fact, an unfortunately placed background star, and the TMR-1c fiasco is commonly used to illustrate the flaws in the publication by press conference model. Our Science paper has languished in obscurity, to the point where one can extract it from behind Science’s formidable pay wall with only a modestly compromising registration agreement to receive e-mail and no money down…

But hope springs eternal. Like everyone else in the community, my eyes lit up upon reading the recent microlensing result that the galaxy is teeming with of order 200 billion rogue planets. Processes like the one that we outlined in our paper may well be operating after all…

It’s Sunday afternoon here in Santa Cruz, meaning that GMT-wise, it’s already June 6th, and the next transit of Venus is exactly one year away. Seems like an appropriate moment to recall a quote by astronomer William Harkness from 1882 (by way of Stephen J. Dick’s Sky and Ocean Joined: The U.S. Naval Observatory 1830-2000).

We are now on the eve of the second transit of a pair, after which there will be no other till the twenty-first century of our era has dawned upon the Earth, and the June flowers are blooming in 2004. When the last transit season occurred the intellectual world was awakening from the slumber of ages, and that wondrous scientific activity which has led to our present advanced knowledge was just beginning. What will be the state of science when the next transit season arrives God only knows. Not even our children’s children will live to take part in the astronomy of that day. As for ourselves, we have to make do with the present.

There’s something oddly appealing about the nonintuitive spacing of Venusian transits, a 243 year repeating pattern, with transits occurring eight years apart, then a gap of 121.5 years, followed by an eight year interval and then a 105.5 year spacing. I’m certainly looking forward to June 6th 2012, when a healthy fraction of the transit will be visible from Lick Observatory on Mt Hamilton. For updates, be sure to bookmark the Transits of Venus Project website, which launched today.

I can’t help feeling uneasy, however, thinking about the state of affairs on Dec. 10-11 2117…

As Mick Jagger famously remarked, you can’t always get what you want. Kepler’s photometric transit observations provide excellent measurements of the planetary orbital periods, the transit epochs and the planet-to-star radius ratios, but they are stingy and tight-lipped when it comes to the planet’s masses, eccentricities, and longitudes of periastron.

Occasionally masses can be inferred from transit timing variations, especially if a system contains more than one transiting planet. Alternately, one can assume a planetary mass-radius relation (keeping in mind, of course, what happens when u assume). For example, M=R^2.06 in units of Earth masses and radii works quite well in our solar system for V-E-S-U-N. Or, dispensing with the trickery, one can pony up and measure radial velocities.

With photometric data alone, information about the orbital eccentricity distribution of the planet census can be deduced by statistically comparing transit durations to orbital periods. The idea is a full elaboration of the simple observation that if a central transit that is substantially shorter than expected, then it’s quite possible that the planet is occulting the parent star near the periastron of an eccentric orbit.

In one of the flurry of Kepler-related papers that accompanied the February data release, Moorhead et al. (2011) implemented just such a program, and generated a statistical analysis of the distribution of transit durations for the Kepler exoplanet candidates. They assumed that the eccentricities conform to a Rayleigh probability distribution function:

where the controlling parameter, sigma, is is related to the mean orbital eccentricity through

To get a sense of what the Rayleigh distributions look like, here are examples for e_av=0.05, e_av=0.21, and e_av=0.50, compared to the distribution of eccentricities in the exoplanet.eu catalog:

Ignoring planets that are likely tidally circularized, the best fit occurs for e_av=0.21. This model, however, underproduces planets at high eccentricity — ‘606 wouldn’t have turned up if e_av=0.21 were a hard truth. Moorhead et al.’s analysis of the Kepler data comes up with plausible best-fit values for e_av ranging from 0.1 through 0.25, for cooler stars with effective temperatures less than 5100K. So there is rough agreement, even though the two catalogs have radically different sampling biases.

A significantly non-zero value for average orbital eccentricity has some interesting consequences for transit surveys. At a given semi-major axis, eccentric planets have (on average) a higher chance of transiting. This is easily seen by comparing an e=0.5 orbit with a circular orbit having the same semi-major axis.

For a population of planets having a specific Rayleigh distribution of eccentricities, the average transit probability at a given semi-major axis is increased by a factor

where the normalization factor, N, is given by

For e_av=0.25, this boosts the total population of planets by about 10% over what one would infer from the standard 1/a circular orbit scaling.

I’ve been reading a textbook on ore-forming processes as part of an attempt to get a little more fluent in geology, and I ran across a plot that is certainly well known to many, but was an eye-opener for me:

The plot charts the solubility by weight of water in several common igneous rocks as one moves deeper into the lithosphere. The take-away message is that even at modest depths, rocks can be very heavily hydrated and are capable of harboring a very large amount of water.

The plot brought to mind something that, to my highly inexpert eye, has always seemed a remarkable coincidence. The volume of water in Earth’s oceans has an average depth of ~4000 meters, leading to a sea-level that does a pretty fair job of outlining the continental margins (which mark the boundaries between denser (but thinner) basaltic crust and lighter (but thicker) granitic crust. Only about 20% of the total continental crust is overlaid by water.

In the extrasolar planet context, an interesting question is whether the situation here on Earth is unusual. Many of the planets that Kepler has found (and will be finding) contain water mass fractions that are considerably larger than Earth’s. Is it reasonable to expect that they’ll have deep oceans that uniformly cover the planets, or is there some sort of mechanism involving water of hydration that maintains a seafloor-continent dichotomy even in the presence of a lot of water? As far as I can tell, this question hasn’t been answered definitively.

The naive answer seems to be along the following lines. Imagine that a terrestrial planet forms in such a manner that the mantle rock is heavily hydrated. Given that mantle rock can easily retain a water mass fraction measured in tens of percents, one could start out with a planet that contains many oceans worth of water, but in which substantial portions of the surface are dry.

When rock melts, the water of hydration is squeezed out. (Migration of this water into the surrounding country rock leads to the mineralized veins that are the basis for many of Earth’s great ore deposits.) On an ongoing volume-weighted basis, most of the melting is taking place beneath the spreading centers that form the mid-oceanic ridges. Every year, of order 300 cubic kilometers of melt are produced, several cubic kilometers of which are erupted to form fresh ocean crust. Coupled with mantle convection, this means that the mantle unburdens its water on a timescale of order a billion years. Some of the water is subducted back down, but this sink is less effective than the source, meaning that the water likely ends up on or near the surface.

So one can imagine planets (perhaps with mantle convection less vigorous than Earth’s) in which continents are gradually submerged as water is squeezed out of the mantle. Not, perhaps, a bad way to go. The world’s best beaches are those of the Seychelles islands — a handful of granitic specks in the vastness of the Indian ocean — the highest peaks of the submerged continental Mascarene Plateau.

Klaus Nomi and David Bowie (Image source and backstory)

I was in the middle of my dynamics lecture this past Monday morning, explaining the Fokker-Planck approximation to the collision term on the right-hand-side of the Boltzmann equation, when my phone started buzzing and vibrating in my pocket. Good thing I had remembered to turn the volume off. Without having to look at who might be calling, I knew it was likely some media outlet, BBC? KCBS? There was a sudden, all-to-familiar sensation of queasy uneasiness which made it very hard to focus on the second-order terms I had just written on the whiteboard.

Back in 2001, I naively and foolishly spoke to a reporter at the London Observer about the “relative ease” of accomplishing strictly hypothetical orbital engineering in the context of a billion-year time frame. The resulting article (now archived by the Guardian) contained an alarmingly incorrect cognitive leap from the ultra-long term to the immediate near-term:

The misconception came exactly at the time when George W. Bush was visiting Europe, explaining his position regarding the Kyoto Protocol. The Observer story became a huge, completely nightmarish story in Europe, which then echoed across the Atlantic, where it was seized upon by the Drudge Report, Rush Limbaugh and others. Here’s an example editorial from the Manchester New Hampshire Union-Leader:

For nearly a week, the story managed to survive, zombie-like through successive news cycles. Eventually, Gary Condit appeared on the scene, and finally, the media’s full attention was diverted elsewhere.

As readers likely know, I’ve been writing on this web log about a planet valuation formula, which is designed to give a quantitative assessment of whether a newly discovered planet is worthy of significant media attention. Last month, I had a detailed conversation with Lee Billings, which was published on BoingBoing as a part of Lee’s series of posts on planets (which are well worth reading!)

Several weeks after the BoingBoing article appeared, I got a very politely worded e-mail from a reporter at News of the World.

[…] I found your article on the value of the Earth which popped up on a UK blog late last week.

From what I can ascertain, your findings and formula haven’t really had the coverage they deserve in the UK media and I was hoping to rectify that…

After a look at the Wikipedia page on News of the World, my heart was pounding. “Wacko US Prof Sez: Sell Earth for 3 Quadrillion Quid!” I sat down at the computer, and it took a long time to compose a reply.

Turned out that the reporter was admirably interested in getting the story right, and the final version (which is behind a paywall) is quite fair. After all, given the possibly arch, arguably pretentious tone here on oklo.org, I did pretty much have it coming.

Predictably, newspapers in Britain saw the News of the World story and immediately picked it up. As is to be expected, successive iterations tend to lose focus on the exoplanets, and gain focus on the value of Earth. Radio stations are calling, trying to set up interviews about how much Earth is worth. Angry e-mails drift into my inbox. Google news is at 61 articles and counting.

I think it’s time to look into installing Google’s AdSense…

Image Source.

In the midst of all that excitement surrounding the Kepler data release, it was easy to overlook the article by Martin & Spruit, Inflated hot Jupiters from merger events, that showed up on astro-ph earlier this month. This paper proposes a sure-to-ruffle-feathers explanation for the radius anomalies of the hot Jupiters. The idea is that stellar mergers (arising from orbital decay in very close binaries) shed angular momentum via an “excretion” disk, from which one or more short-period giant planets manages to form. In this picture, short-period, anomalously inflated planets are large because they are young — their formation dates to the binary star merger that created their parent star, and they are headed inward for destruction on timescales significantly shorter than the typical several-billion year age of planet-bearing main-sequence stars.

Image Source: Tylenda et al. 2010.

It’s believed that the anomalous novae V1309 Sco (which occurred in 2008) and V838 Mon (which made a big splash in 2002, and whose light echo is shown in the image at the top of the post) were both caused by binary mergers. In the case of V1309 Sco, the more massive of the two progenitor stars was probably similar in mass to the Sun, whereas for V838 Mon, a primary of order 8 solar masses was involved. Numerical simulations, such as the ones shown below by D’Souza et al. (2006), suggest that two distinct stars merge into a single star surrounded by a disk-like structure over an action-packed phase that lasts ~10 orbits.

The idea that merging stars can give rise to planets shows up prominently in the literature in the 1980s, with a series of papers in Soviet Astronomy by A. V. Tutukov, who had a number of speculative ideas regarding planet detection and planetary systems that have turned out to be quite on the mark — he did detailed calculations of the prospective yield of M-dwarf transit surveys, and he argued that ~25% of stars should harbor planetary systems. In several papers (including here) he advocated the idea that excretion disks can give rise to planet formation.

It occurred to me that in the event that stellar mergers do indeed serve as an effective formation channel for short-period planets, then blue stragglers should be very high-grade ore for photometric transit searches. The blue stragglers are main-sequence stars in globular clusters that lie above the main-sequence turn-off in the Hertzsprung-Russell diagram, and which are generally found near the cluster core. It’s believed that they owe their relative youth to being the product of binary mergers.

One of the most important early exoplanet-related results was the Gilliland et al. 2000 HST photometric survey of the rich nearby globular cluster 47 Tucanae. The Hubble telescope was trained on the cluster for 8.3 days, and time-series photometry (taken through two filters) was analyzed for ~34,000 individual stars. If the occurrence rate of hot Jupiters in 47 Tuc was similar to the occurrence rate in the solar neighborhood, then 17 transit planets were to be expected. None were found. This null result is generally attributed to the cluster’s low metallicity and to the possibility that planet formation was inhibited by the dynamical interactions and intense UV radiation that occurred during the cluster’s star formation phase.

A close up look at the 47 Tucanae color-magnitude diagram indicates that the 2-color HST imaging of cluster contains about twenty blue stragglers. Interestingly, it’s not entirely clear whether the blue stragglers have been folded for transits. In the Gilliland et al. 2000 paper, it appears that only the conventional main-sequence stars in the cluster were included in the analysis. The paper states: “For the results discussed further below only the 34,091 stars falling within a bright main-sequence box as shown were analyzed for time series.”

If hot Jupiters are commonly forming from binary merger events, then it seems like there should be a good chance that there could be a transit among the 20-odd blue stragglers observed with HST. Because this handful of stars are much smaller than the red stars at the same luminosity, the transit depths could likely be detectable, given the quality of the HST photometry and the brightness (I=16-17) of these stars. If the planet occurrence rate for merger remnants is 50% one would expect to find one transit among the tweny stars, given the ~10% a-priori geometric probability of transit. As a first step, certainly, it’ll be interesting to see whether these stars were analyzed in any of the follow-up work that was done with the Gilliland et al. dataset.

Earlier this year, in the New York Times Magazine, there was a very lengthy, very glossy advertising insert devoted exclusively to high-end watches. I leafed idly through it, and picked up a new concept, that of a complication. Where watches are concerned, a complication refers to any feature that goes beyond the simple display of hours, minutes, and seconds. According to the Wikipedia,

The Patek Philippe Calibre 89 is a commemorative pocket watch created in 1989, to celebrate the company’s 150th anniversary. Declared by Patek Philippe as “the most complicated watch in the world”, it weighs 1.1 kg, exhibits 24 hands and has 1,728 components in total, including a thermometer and a star chart. Made from 18 carat (75%) gold, it has an estimated value of $6 million, and took 5 years of research and development, and 4 years to manufacture. Four watches were made; one in white gold, one in yellow gold, one in rose gold and one in platinum.

The Calibre 89’s complications include such must-haves as the equation of time (yielding the instantaneous difference between apparent solar time and mean solar time), the date of Easter, and a 2800-star celestial chart. And just imagine the convenience of being able to pull your 2.42 lb watch out of your pocket whenever the need strikes to see what century it is!

It occurred to me that the 1,235 Kepler candidates could conceivably provide a bonanza for the high-end mechanical watch industry. The candidates, with their particular periods, transit durations, transit depths, effective temperatures, and radii offer endless opportunities for unique horological complications. In this spirit, at the link below, I’ve made a 1,235-complication applet which charts the appearance and disappearance of transits, timed from the start of Kepler’s Q0. The horizontal direction is mapped to orbital period, and the vertical direction is mapped to M=R^2 in Earth units. It’s mesmerizing to watch…

Click here to watch the animation.

The planet — host star metallicity connection has been one of the most secure and enduring results from the radial velocity planet surveys. In 1997, soon after the detection of the first planets, Guillermo Gonalez pointed out that the host stars were significantly enriched in elements heavier than hydrogen and helium, and suggested that a planet-metallicity connection exists.

Over the years, the correlations have been refined by many different workers, and a clear set of facts has emerged:

(1) Giant planet hosts, all the way from low-mass red dwarf stars through stars that are somewhat hotter and more massive than the Sun, tend to be metal rich.

(2) The occurrence rate for giant planets increases with stellar mass.

(3) Among stars with mass similar to the Sun, there’s no evidence that the presence of sub-Neptune/super-Earth is correlated with host star metallicity.

Taken together, these facts provide basic support for the core-accretion mechanism of giant planet formation. A planet like Jupiter forms by first assembling a core of icy/rocky/metallic material. When the core mass grows to of order 10-20 Earth masses, the core gains the ability to very rapidly accrete hydrogen and helium, and increases its mass by a significant, multiplicative factor to become a full-blown giant planet. Core accretion is a threshold phenomenon in the sense that the eventual presence or absence of a giant planet depends sensitively on whether the core is assembled while nebular gas is still present. Sufficiently rapid core growth is strongly aided by larger disk masses (which is the source of the planet-stellar mass connection) and by larger surface densities of solids in the disk (which is the source of the planet-stellar metallicity connection).

“Better late than never.” You hear that a lot when the chronic under-performance of super-Earths and sub-Neptunes is being discussed. The planet census makes it clear, however, that when not pressured to succeed while the gas is still there, sub-Neptunes and super-Earths regularly grow to 5-15 Earth masses and migrate to various locations in protoplanetary disks. The observations, furthermore, show that for host stars lying close to a solar mass, there’s no evidence for any metallicity dependence in the occurrence rate of these lower-mass planets.

At some point, however, metallicity has to play a role. An early-bird Population II star with [Me/H]=-3 started out with only ~0.1% as much iron, molybdenum, oxygen and carbon as did the Sun. Super-Earths won’t be found orbiting such stars because the raw planet-building materials flat-out weren’t there. Likewise, for low-mass disks orbiting low-mass stars, the overall metal budgets are tight enough that it’s quite reasonable to expect that a planet-metallicity connection for non-giant planets should be detectable.

Last year, Kevin Schlaufman and I looked into this issue and we found a tantalizing hint that among the red dwarf stars, a planet-metallicity connection does exist for planets with ~Neptune mass and below. The statistics were too sparse, however, to have anything more than ~1-sigma confidence.

Enter the Kepler results. In the course of an afternoon, 1,235 planet candidates flooded the market, completely upending the old business-as-usual model for the planet hunters. Correlations no longer emerge, they pop out.

In addition to being numerous, the Kepler stars are quite well characterized, and Sloan photometry has been published for the ~150,000 stars with Q1+Q2 public-domain light curves. At a given J-H color (obtained from the 2-Mass catalog) a star’s Sloan g-r color is significantly dependent on metallicity (see, e.g. here). It’s thus informative to make J–H — g-r color-color plots with (1) a control sample of 10,000 stars drawn from the Kepler 156K star target list, (2) the Kepler giant planet (Rp>5R_earth) hosts, and (3) the Kepler low-mass planet (Rp<5R_earth) hosts:

These plots, which are from a paper that Kevin and I just submitted to the Astrophysical Journal, demonstrate quite convincingly that a metallicity correlation does exist for low-mass planets orbiting lower-mass stars. (The correlation starts to kick in below ~0.8 solar masses.) Assuming that the probability of forming a planet is proportional to the total amount of solids in its protoplanetary disk, the correlation indicates that a late K-dwarf with 70% of the Sun’s mass needs to have a metallicity [Fe/H]=0.15 to have the same chance of forming a planetary system as a solar metallicity star of similar mass.

I’m pretty excitied about these results. A quantitative statistical link between relative disk conditions and planet outcomes for the huge super-Earth population gives us direct information about how the really interesting systems — the ones harboring large terrestrial planets — are assembled.

We’ll put the paper on astro-ph once it’s gone through review. It contains a lot of work to establish that the correlations are real, rather than due to reddening or the various observational biases inherent in the Kepler target list.

Last August, SFMOMA put on an exhibition that featured a number of Chuck Close’s hyperrealistic portraits. It was interesting to study the sudden transition between a patchwork of acrylic brush strokes, as in the cell-phone close-up snapshot just above, and an image that makes sense as a whole.

The recent public release of the Kepler data triggers an effect that’s a bit like stepping back rapidly from one of Close’s portraits. Suddenly, a huge swath of the planetary distribution connects with a larger picture. This effect holds especially true when one looks at the list of systems that harbor multiple transiting candidates.

With the census of radial velocity planets, it’s often quite difficult to determine whether a signal is originating from a single planet on an eccentric orbit, or a pair of planets participating in 2:1 resonance. The only really well-characterized unambiguously resonant RV system is Gliese 876, where the combination of large Ks, a long observational base, and rapidly unfolding 30-60-120d orbits has allowed the dynamics of the resonance to be revealed in detail.

The 115 Kepler two-transit systems indicate right away that systems like Gliese 876 are intrinsically rather rare. In the illustration below, I’ve taken each of the two-transit systems, and identified the larger member of the pair. I’ve then plotted the period ratio, P_small/P_large as the x coordinate, the parent star’s mass as the y coordinate, the temperature of the planets as a grayscale (saturating to white at 1500K), and the sizes of the symbols in proportion to the observed radii.

The immediate impression from the diagram is that the systems are not overwhelmingly clustered around the simple integer commensurabilities. Low-order mean-motion resonances among the extrasolar planets are the mild exception, and not the rule.

That said, the resonant systems are clearly present. Of the forty 2-transit systems with inner-outer period ratios lying between 2.0 and 3.0, six of them have period ratios between 2.02 and 2.05. The chances of a concentration like this occurring purely by chance is considerably less than 1%. Furthermore, the fact that the clustering occurs a percent or two above the exact 2:1 commensurability can be understood in terms of the dynamics of resonance. When one has two massive planets deep in a resonance, with a significant angular momentum deficit, then the system apse precesses in a retrograde direction (as is the case with Gliese 876). The resonance is controlled by a restoring force that drives conjunctions to occur at periastron. This means that if one observes along a fixed line of sight, then the inner planet is seen to orbit a bit more than two times as often as the outer planet.