NOAA Weather prediction is performed continuously by two IBM Power 575 Supercomputers named Stratus and Cirrus, each carrying out 69.7 trillion calculations per second. These machines each run 20 concurrent models for a global ensemble forecast. Approved production models run on Stratus, and development codes run on Cirrus. Huge volumes of this-just-in updates to the world’s atmospheric conditions pour in constantly from satellites, radiosondes, aircraft, ships and ground stations. The resulting predictions tend to be pretty good to about five days out:

Weather prediction would get a lot harder if the atmosphere was partially ionized. Not only would the ground stations melt, but the wind would no longer be able to blow freely through Earth’s magnetic field lines, which in turn would start to behave like rubber bands that resist being stretched and squeezed. The charged wind, furthermore, would experience Ohmic resistance that would create local heating.

On hot Jupiters, temperatures are high enough so that atmospheric alkali metals such as sodium and potassium are starting to ionize. This effectively guarantees that it’s necessary to do radiation magnetohydrodynamics in order to understand how these planets really work.

In a paper published last year, Konstantin Batygin and Dave Stevension showed that Ohmic dissipation is a very attractive mechanism for providing an extra energy source that inflates hot Jupiters and contributes to the bizarre range of radii exhibited by the transiting planets (radii that have caused a lot of consternation among those who tend to worry about such things).

Konstantin’s paper got me thinking about ways to test the Ohmic dissipation hypothesis. I wrote up some initial thoughts in this post from last summer. I’ve since worked things out further in collaboration with UCSC Physics Undergrad Matteo Crismani and with Fred Adams. We have a new paper on the topic that’ll be up on astro-ph later today.

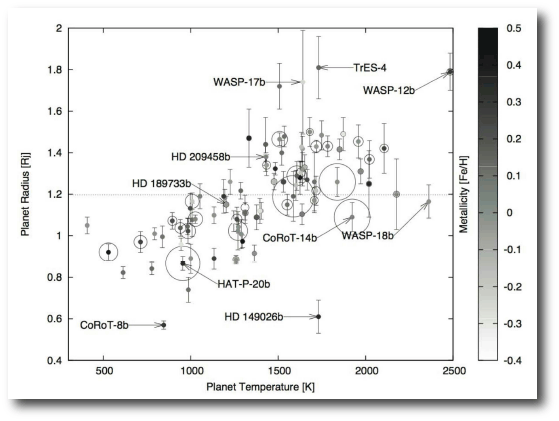
We started with the data in the plot shown above, namely the disparate collection of transiting planets with well-measured masses and radii. We computed the radius anomaly for each of these planets, that is, the difference between a plain-vanilla structural model for a solar-composition planet with the observed mass and insolation and the actual observed radii.

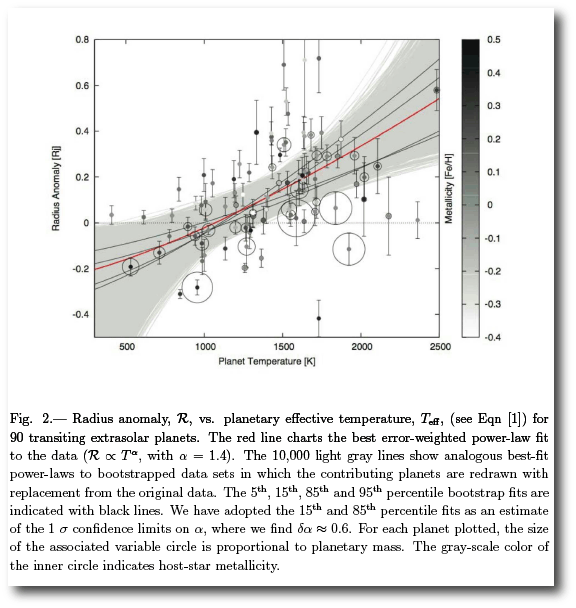
These radius anomalies show a strong correlation with the amount of energy that they receive from their parent stars. If one examines power-law fits, it turns out that radius anomalies scale with temperature to the 1.4+/-0.6 power.

Our bottom line is that this power-law dependence is very much in line with what one might expect from Ohmic heating (if the back reaction of the magnetic field onto the wind speed is taken into account), and my guess is that Batygin and Stevenson have taken out a large chunk of the radius problem. (See also, their very recent follow-up paper with Peter Bodenheimer).

Our paper contains several pages of details that might not be appropriate for a family-oriented site such as oklo.org, so if you’re interested, then by all means download the .pdf and have a look…