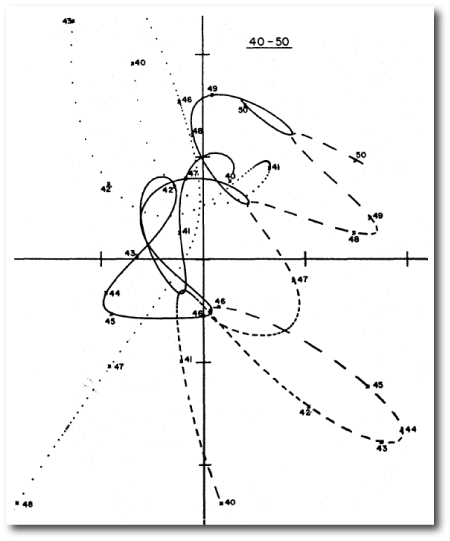
More than a decade ago, Fred Adams and I wrote a paper that wallowed into the slow motion disasters that can potentially unfold if another star or stars passes through the solar system.

Here’s the abstract:

Planetary systems that encounter passing stars can experience severe orbital disruption, and the efficiency of this process is enhanced when the impinging systems are binary pairs rather than single stars. Using a Monte Carlo approach to perform more than 200,000 N-body integrations, we examine the ramifications of this scattering process for the long-term prospects of our own Solar System. After statistical processing of the results, we estimate an overall probability of order 2×10^5 that Earth will find its orbit seriously disrupted prior to the emergence of a runaway greenhouse effect driven by the Sun’s increasing luminosity. This estimate includes both direct disruption events and scattering processes that seriously alter the orbits of the jovian planets, which force severe changes upon the Earth’s orbit. Our set of scattering experiments gives a number of other results. For example, there is about 1 chance in 2 million that Earth will be captured into orbit around another star before the onset of a runaway greenhouse effect. In addition, the odds of Neptune doubling its eccentricity are only one part in several hundred. We then examine the consequences of Earth being thrown into deep space. The surface biosphere would rapidly shut down under conditions of zero insolation, but the Earth’s radioactive heat is capable of maintaining life deep underground, and perhaps in hydrothermal vent communities, for some time to come. Although unlikely for Earth, this scenario may be common throughout the universe, since many environments where liquid water could exist (e.g., Europa and Callisto) must derive their energy from internal (rather than external) heating.

As one might expect, our scholarly efforts generated only a middling interest from the astronomical community, which soon faded and froze altogether. Science writers, on the other hand sometimes run across the article and write with questions.

I am doing a piece on rogue planets and the scenario that earth might become a rogue planet. I have found some stuff on this on the web and learned that you have done some research on rogue planets.

1. Why do you think rogue planets are so interesting?

From an aesthetic standpoint, there’s something compelling about a world drifting cold and alone through the galaxy, or even through intergalactic space. From a more practical standpoint, if rogue planets are common (as it appears may possibly be the case from the micro-lensing results) it is possible that the nearest extrasolar planet is not orbiting a nearby star, but is rather travelling through the Sun’s immediate galactic neighborhood, say within a few light years of the solar system.

2. Could earth become a rogue planet, and is there any guess, how probable this is? Let’s assume it would happen, what would most probably be the reason for that?

Earth could become a rogue planet if the solar system suffers a close approach by another star (or binary star). If another star passes within ~1 Earth-Sun distance from the Earth, then there is a good chance that the Earth would wind up being ejected into interstellar space. Fortunately, close encounters between stars are extremely rare. There is about a 1/100,000 chance that Earth will suffer this fate during the next five billion years. Those are very low odds, so in the grand scheme of things, we are in an extremely safe position. If we scale the galaxy down by a factor of ~10 trillion, then individual stars are like grains of sand separated by kilometers of empty space, and moving a meter or so per year. It’s clear that in such a system, a sand grain will drift for quite a long time before it comes close to another sand grain.

3. Could you speculate on how a human being on earth would experience the process of earth being kicked out of the solar system?

There would be plenty of warning. With our current capabilities for astronomical observation, the interloping star would be observed tens of thousands of years in advance, and Earth’s dynamical fate would be quite precisely known centuries in advance. The most dramatic sequence of events would unfold over a period of about two or three years. Let’s assume that the incoming star is a red dwarf, which is the most common type of star. Over a period of months the interloping star would gradually become brighter and brighter, until it was bright enough to provide excellent near-daytime illumination with an orange cast whenever it is up the sky by itself. It’s likely that the size of its disk on the sky would become — for a few weeks — larger than the size of the full moon, and vastly brighter. Like the Sun, it would be too bright to look at directly. After several more months, one would start to notice that the seasons were failing to unfold normally. Both the Sun and the Red Dwarf would gradually draw unambiguously smaller and fainter in the sky. After a year, the warmth of the sun on one’s face would be gone, and it would be growing colder by the day… Over a period of several more years, the Sun would gradually appear more and more like a brilliant star rather a life-giving orb. A winter, dark like the Antarctic winter, but without end, and with ever-colder conditions would grip the entire Earth.

4. What do you expect, how long humans could survive such an incident?

The Earth could not support its current population, but with proper planning, a viable population could survive indefinitely using geothermal and nuclear power. We would literally have a thousand years or more to get ready. Certainly, there are much worse things that could happen to humanity.

5. Would any life on earth survive?

Earth would effectively become a large space-ship, and with proper planning, a controlled biosphere (like in a large space colony) could be maintained. Were there no intelligent direction of events, and the Earth was simply left to its own devices, then surface life would freeze away, but the deep biosphere (the oil field bacteria, the deep sea vents, and other other biomes not directly dependent on solar energy) would persist for millions, if not tens of millions of years.

6. What do you think are chances that we will find an earthlike rogue planet?

This depends on what one means by “earthlike”. If one means a planet with Earth’s mass, at very large distance, say thousands of light years, the chances are very good that we will get micro-lensing detections within a decade or so. The data returned, however, will consist only of the likely masses of the planets. Nothing else.

I would estimate that the chances of finding a rogue Earth-mass planet within a potentially reachable distance, say within a light year, are about 10%. The chances, however, that this planet will have an interesting frozen-out surface environment that would please a Hollywood screenwriter are effectively zero. Most rogue planets get ejected from their systems very early in their parent star’s history, long before really interesting things have had a chance to happen from an astrobiological perspective.

This was no fruit of such worlds and suns as shine on the telescopes and photographic plates of our observatories. This was no breath from the skies whose motions and dimensions our astronomers measure or deem too vast to measure. It was just a colour out of space—a frightful messenger from unformed realms of infinity beyond all Nature as we know it; from realms whose mere existence stuns the brain and numbs us with the black extra-cosmic gulfs it throws open before our frenzied eyes.

H.P. Lovecraft, The Colour out of Space Amazing Stories, Vol. 2, No. 6 (September 1927), 557–67.

I’ve always thought that the Colour out of Space was H.P. Lovecraft’s best effort. One can argue about economy of expression, but the story is nearly unmatched in its attempt to confront — and imagine — the truly alien.

I think we currently have substantially less understanding of the extrasolar planets than is generally assumed. Thousands of planets are known, but there is no strong evidence that any of them bear a particular resemblance to the planets within our own solar system. There’s always a tendency, perfectly encapsulated by the discipline of astrobiology, with its habitable zones and its preoccupation with water — to make wild extrapolations into the complete unknown.

An interesting synopsis of much of what we do know can be gained by looking at the latest mass-radius diagram for the exoplanets. The number of planets with joint mass and radius determinations is growing rapidly, and the elastic virtue of a log-log plot fails to suppress the huge range in apparent planetary structures. To within errors, it appears that 6-Earth Mass planets range in radii by a factor of at least three. This is impressive, given that constant density implies R~M^{1/3}…

On the figure, I’ve plotted three potential mass-radius relations for super-Earths. This first (in Earth units) is the standard-issue M=R^{2.06} fit that one gets from the solar system planets (excluding Jupiter). The second (again in Earth units) is the vaguely alarming M=3R relation suggested by Wu & Lithwick’s transit timing analysis. The third mass-radius relation is what one might expect if planets form in-situ and accumulate low-density hydrogen envelopes around rocky cores. (Evaporative mass loss makes this more of an upper limit). Frustratingly, all three relations remain plausible.

It’s thus fantastic news that NASA’s TESS Mission has been selected for flight. TESS will find effectively all of the transiting Super-Earths orbiting the few million brightest stars, and with dedicated ground-based radial velocity follow-up, will — less than a decade from now — allow for a fantastically detailed version of the above plot.

Tau Ceti has street cred. Lying only 11.9 light years away, it is the second-closest single G-type star. It’s older than the Sun, and photometrically quiet. It’s naked-eye visible from both hemispheres, ensuring VIP seating at any SETI fundraiser.

And so what about planets? It’s been clear for a few years that Tau Ceti has a zeroth-order dissimilarity with the solar system. That is, if it had a Jovian-mass planet in a Jovian-like orbit, a press conference would have been dedicated to it several years ago. Indeed, because it is so bright and so quiet, Tau Ceti is among the handful of stars in the sky that are best suited to long-term high-precision monitoring via the Doppler velocity technique. It’s at or near the top of the list for all of the major Doppler surveys.

Tau Ceti displays a marked excess luminosity in the far-infrared. Blotchy sub-millimeter images imply that this excess luminosity arises from a wide ring of cold dust at Pluto-like distances from the star. In this picture, the radiating dust arises from ongoing collisions within a Kuiper belt-like disk comprising roughly an Earth-mass worth of icy asteroidal bodies:

Tau Ceti’s Kuiper belt seems to be about ten times more massive than our own Kuiper belt, despite the fact that Tau Ceti’s metallicity is only about one-third that of the Sun. There’s little risk in hypothesizing (read hand-waving) that the low metallicity of Tau Ceti’s protoplanetary disk meant slow growth for Tau Ceti’s retinue of proto-Jovian cores, which subsequently missed out on rapid gas accretion. The ensuing presence of Neptunes, and the concomitant absence of a Jupiter, generated a different dynamical history compared to the Solar System’s — namely one with more stuff left over at the end of the day in the icy outer reaches.

Given this picture, the a-priori odds are excellent that Tau Ceti resembles tens of billions of ordinary, single Population I stars in the galaxy and also harbors multiple inner planets with masses between Earth and Neptune, on nearly circular, nearly co-planar orbits with periods of 100 days or less. Should such worlds exist in orbit around Tau Ceti, then it’s likely that sufficient radial velocity data now exist to dig them out…

Readers surely noticed the paper by Mikko Tuomi and colleagues that was posted to astro-ph earlier this month. Tuomi and collaborators report on a joint analysis of three large-N data sets that comprise thousands of radial velocity measurements (from HARPS, KECK and AAT) spanning a total time base line in excess of 13 years. Ideally, one would like have a fully definitive conclusion emerge from such a massive data set, but frustratingly, Tau Ceti is holding its cards very close to the vest, and as radial velocity half-amplitudes inexorably drop below K=1 m/s, this will be an increasingly common behavior from other nearby high-value stars. In their arXiv preprint, Toumi et al. lay off their risk and remain ambiguous regarding actual detections of actual planets, providing only a fully hedged speculation at the end of the abstract, that these “periodicities could be interpreted as corresponding to planets…”

The modeling strategy for Tau Ceti taken in the Tuomi et al. paper provides an alternative to the approach adopted by Dumusque et al. in digging the K=0.5 m/s Alpha Cen Bb out of a similarly challenging data set. For both systems, the authors adopt the stance that it is no longer sufficient to write off excess scatter in radial velocity fits as “stellar jitter”. Dumusque’s team developed a physical model for starspot activity migrating latitudinally on a differentially rotating star, and also modeled the convective blueshift arising from stellar activity. Application of these physical models spurred the removal of systematic “noise” from the time series, thereby revealing a candidate Earth-mass planet in a 3.2-day orbit. Tuomi et al. excavate five potential planets by exploring the use of ARMA(p,q) — AutoRegressive Moving Average — models which recognize that (in addition to a Keplerian signal) both the value of given velocity measurement as well as its accompanying error are potentially correlated with previous measurements. ARMA models and their generalizations, ARCH, GARCH, NGARCH, etc., are an old standby for modeling financial time series. Near-term VIX predictions anyone?

Indeed, planet detection and trading have certain similarities. Noisy signals, non-stationary processes, cut-throat competition, and the opportunity to land yourself in the media spotlight when things go awry.

And the possible planets? Should the signals isolated by Tuomi et al turn out to be both real and Keplerian, then Tau Ceti will join the legions of stars in the galaxy that harbor fully ordinary planetary systems.

Galileo’s unveiling of Io, Europa, Ganymede and Callisto is unarguably shortlisted for the most important astronomical discovery of all time. The Galilean satellites constitute a planetary system in miniature, and their clockwork presence is a centerpiece of Newton’s De mundi systemate.

And indeed, if one bases one’s expectations for exoplanetary systems on the Jovian satellites (as well as the regular satellite systems of Saturn and Uranus) then the startling abundance of compact systems discovered by the Geneva Team and by Kepler are hardly startling at all. The Galaxy’s default planetary system — as expressed around many, if not most of its stars — has a handful of planets on near-circular orbits, with periods ranging from days to weeks, and masses of order one part in ten thousand of the central star. Out here in the sticks, near the Sun, we’ve got an Earth, yes, but unlike most stars, we have no super Earths.

There is an intriguing, seemingly anti-Copernican disconnect between the solar system and the extrasolar planets. Much of the theoretical framework of planet formation is based on the paradigm provided by the Minimum Mass Solar Nebula (MMSN), the $\sigma \propto r^{-1.5}$ disk of net solar composition that is required to account for the solar system’s planets. In the standard formulation, the MMSN holds its power-law form inward to about 0.5 AU, where it meets a murkily indistinct inner boundary that’s needed to account for the lack of anything interior to Mercury’s orbit.

Interestingly, the MMSN fades out just where the super-Earths really start to appear. This has led to the widespread assumption that planets somehow form at large radii and then migrate long distances in order to be found in their observed orbits. That seems rather odd.

Eugene Chiang and I have been exploring an alternative idea — namely that the solar system doesn’t present a good starting template for studying extrasolar planets, and that planets, in general, don’t migrate very far (if at all). Could it be that the huge population of super-Earths formed right where they are observed? If that’s the case, it makes life simpler, and it implies that the template we’re after is the Minimum Mass Extrasolar Nebula (MMEN), which can be defined by grinding up the planets that have been observed by Kepler, and which is not all that different from what one gets if one simply takes the MMSN and runs it all the way into the dust sublimation boundary at ~0.05 AU.

Our paper is available at arXiv.

A few weeks ago, I got an e-mail from a reporter related to a story that will feature favorite space photos:

We’re hoping some space-themed photo comes to mind, either a picture taken by a space telescope, or by yourself from your own backyard, or anything else that relates to space. We’d also welcome any comments about the photo’s meaning to you.

I think my favorite space photo is the Voyager image of the crescent Neptune and Triton.

For two reasons. First, there’s no false color, no artifice, no agenda. This photograph is calming, mysterious and aesthetically perfect.

Second, the image is dominated by the night side of Neptune. Implicit in the photograph is the amazing fact that it was taken from a vantage that was further than the Sun than the planets. Less than one Neptune orbit elapsed between its discovery in 1846 and the Voyager flyby in 1989. A crescent Neptune seems to me far more subtly profound than the iconic “pale blue dot” image taken by the same spacecraft not all that long thereafter.

Image source: Drew Detweiler

The Pythagorean version of the gravitational three-body problem is very simple to state.

Assume that Newtonian Gravity is correct. Place three point bodies of masses 3, 4, and 5 at the vertices of a 3-4-5 right triangle, with each body at rest opposite the side of its respective length. What happens?

This particular problem seems to have been first posed in the late 1800s by the German mathematician Meissel, who mysteriously asserted that the motion of the three bodies should be periodic. That is, he felt that they would come back to their exact starting positions after executing a complex of intermediate motions. A first attempt at the solution — using numerical integration with a variable stepsize — was published in 1913 by Carl Burrau. He was able to map out the intial trajectories through several close encounters, but he was unable to integrate far enough to determine what eventually happens.

The correct solution was found in 1967 by Szebeley and Peters, who used the technique of three-body regularization to resolve the succession of close encounters. Here’s one of their diagrams showing a segment of the complicated motion.

The Szebehely-Peters paper is fun to read. It emphasizes that this nonlinear problem is surprisingly tricky to solve, and that it shows the classic sensitive dependence on small variations in the initial conditions. For example, here’s a link to a recent, attractively rendered YouTube video that animates the trajectories and osculating orbits, as obtained via an implementation that uses Mathematica’s NDsolve.

Screenshot source.

Unfortunately, however, a careful analysis shows that the motion from 2:47 through the end of the video is completely incorrect…

I’ve always been struck by the fact that there’s a fascinating subtext to the trajectories of the three bodies if they are interpreted as a narrative of interpersonal relations. An initial value problem for a set of six coupled, first-order ordinary differential equations unfolds to telegraph a drama of attraction, betrayal, redemption, triumph and loss.

This summer, I had an opportunity to collaborate on the development of a scored, choreographed 3-minute 45-second performance of the problem which was premiered last month at the ZERO1 Biennial in San Jose. Our goal was to simultaneously convey the interpretive subtext while adhering to an fully accurate set of trajectories. It took a lot of work and was quite an intense experience. From the description at the ZERO1 site:

Three dancers in illuminated costumes create a live video visualization of the elliptic-hyperbolic solution to the classic Pythagorean three-body problem. A custom light tracing application detects light emitted from LEDs on the dancers’ soft circuitry costumes to create a visual model of their trajectories across the 2D plane of the stage. This realtime graphic visualization is projected on a large screen behind the stage in order to provide the audience with a birds eye perspective of their complex motion.

The use of digital technologies presents challenges for contemporary choreographic methods as data visualization guides movement through performative space on scientifically accurate trajectories. Live accompaniment from three musicians enhances physical performance as each body is interpreted through movement and sound. Feelings of longing, connection, and isolation are intertwined as the bodies are flung apart by the same gravitational forces that draw them together.

(That last sentence could more properly read, The bodies are flung apart despite feeling only attractive gravitational forces.)

To give a better sense, here are some notes and diagrams from mid-way through the process, as the choreography and the rehearsals were beginning to gel.

It’s particularly fascinating how the immediate outcome of the near-return to the pythagorean condition at the halfway mark is so different from how things unfold at the start of the piece. I like the interpretation that body 4 is somehow lazy at this point, or late to realize the import of the situation, and is marginalized as a result. This is the first real opportunity for bodies 3 and 4 to express emotion — shock for body 4, joy for body 3.

In the following measures, body 4 is marginalized, sulky, scheming, whereas body 3 is doing its best to impress, in the set of looping, private engagements. A reverie! The successive body 3-5 interchanges should _highlight_ the difference in masses between 3 and 5. Body 3 is light footed, fleet, body 5 glides smoothly, deliberately, (but not dully) as an anchor.

Body 4 must come back from its runout with a renewed sense of determination and purpose. The ensuing encounter between 4 and 5 must somehow convey 4’s charms and strengths. In a very real sense, this encounter is the tipping point that determines the outcome for all time. This is where the youtube video went off the rails.

As a consequence, there should be a sense of unfulfillment in the next body 3-5 encounter (a grasp, a gaze that fails to connect?) which sets up 3 to dive through on the way to its penultimate run-out. In this sequence, body 3 must somehow fail to live up to the expectations that it so brightly promised. The outcome is now determined, and the bodies know it, although the audience doesn’t.

While body 3 is at the arc of its final run-out, body 4 is weaving a spell on body 5, cementing the outcome ever more decisively. Indeed, Body 5 is only briefly engaged as 3 makes its final dramatic run through body 4 and 5’s orbit. The final sequence of encounters between body 4 should grow ever more identical, signaling the finality of the outcome.

Full-size (1536×2048) .gif images: one, two.

We went up to Mount Hamilton yesterday afternoon, and, as was the case for everyone who saw the transit, it was a unique conjunction of time, place, and circumstance.

The Lick Observatory staff deployed the historic 36-inch refractor to extraordinary advantage. Rather than project the image, which has the effect of divorcing the instrument from the event, they removed the eyepiece and stretched a cloth across the focal plane. The resulting effect, somehow, was to seamlessly integrate the transit into its surroundings and its historical context, 1639, 1761, 1769, 1874, 1882, 2004, 2012…