So when presented with that particular formulation, I generally prefer to get the bad news first:

Stefano Meschiari and I have investigated how the new radial velocity data for the HAT-P-13 system affect the possibility of measuring transit timing variations for the short-period planet “b” as the heavy, long-period planet “c” rumbles through its periastron passage later this spring.

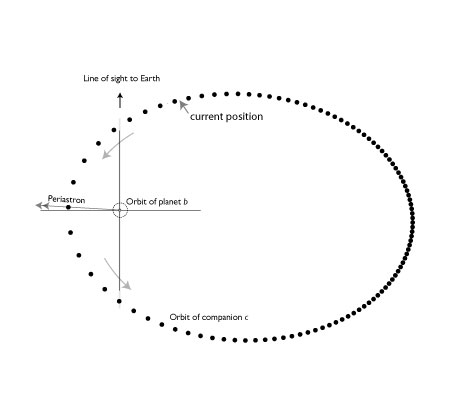
First, recall the overall set-up. HAT-P-13 was discovered in transit by Gaspar Bakos and his HAT Net collaborators last summer. HAT-P-13 “b” is a standard-issue hot Jupiter with 0.85 Jupiter masses and a fleeting 2.916-day orbital period. The radial velocity follow-up indicated that the system also contains an Msin(i)~14.5 Jupiter mass object on an eccentric orbit with a P~430 day period. If the two planets are close to coplanar, then the system should have tidally evolved to an eccentricity fixed point — a configuration that allows one to extract Juno-mission style interior information from the inner planet for free.

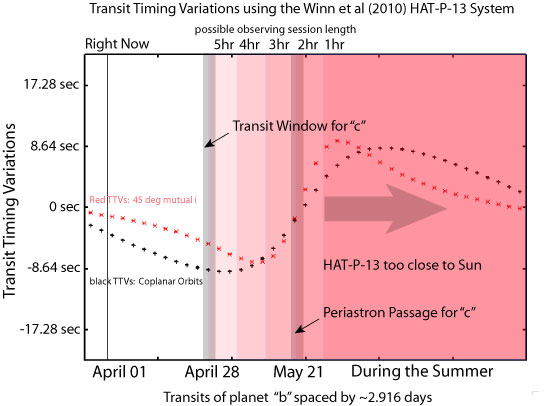
System Version 1.0 for HAT-P-13 generates significant transit timing variations for the inner planet during the weeks surrounding the periastron passage of the outer planet. In a post two weeks ago, I showed some invigorating calculations by Matthew Payne and Eric Ford, which charted the details of the timing variations. Here’s a figure inspired by the Payne-Ford analysis that uses the systemic console’s TTV routines to zoom in on the imminent HAT-P-13 periastron:

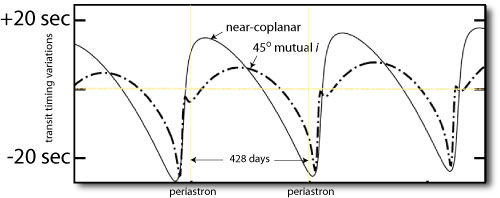
The above picture is quite rosy, at least as far as the outlook for TTVs is concerned. With orbital models that are based on the Bakos et al. discovery data for the system, the transit-to-transit time intervals for planet b veer from ~17 seconds shorter than average to ~17 seconds longer than average (relative to the long-term mean) as planet c runs through its periastron and exerts its maximum perturbing influence. This shift from a compressed period to an expanded period occurs rather abruptly over a span of about 2 weeks. Most provocatively, there are significant and feasibly observable differences between the TTV profiles produced by the coplanar configuration and by the configurations with 45-degree mutual inclinations. And finally, all the action was predicted to occur just before the end of HAT-P-13’s yearly observing season (see Bruce Gary’s revived AXA page for wealth of additional detail). It’s not hard to revel in the thought of all the ground-based observers pooling their results (in the spirit of 1761 and 1769) and emerging with a big-picture result!

The new Winn et al. data, however, definitely rain on the TTV parade. The augmented (out-of-transit) data set now shows that the period of planet c is about 20 days longer than previously believed, and c’s eccentricity also drops slightly, from e_c=0.69 to e_c=0.666. With the new orbital model, the differences in the TTVs generated by the co-planar and mutually inclined configurations are considerably smaller. The overall amplitude of the variations is cut nearly in half, and the excitement is pushed far more precariously against the end of the observing season:

And the good news? As described in the last post, the Winn et al. data show that the orbital plane of planet b is probably aligned with the equator of the parent star, which, in turn, means that it’s quite likely that the b-c system is indeed coplanar.

If we assume coplanarity, then the system should be at an eccentricity fixed point in which the apsides of the two planets are aligned. A measurement of the eccentricity of planet b then allows the interior structure and the tidal dissipation of planet b to be measured.

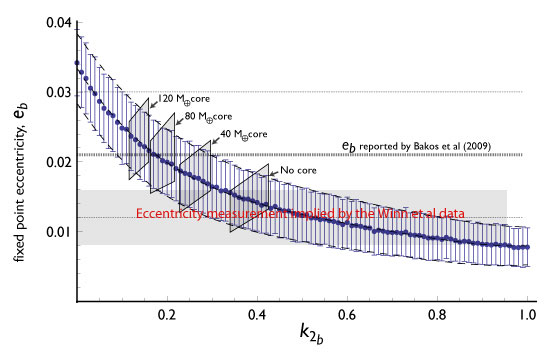
The augmented radial velocity data set permits a better measurement of planet b’s orbital eccentricity. Figure 5 of the Winn et al. paper has the relevant plot, which shows the distribution of Markov-Chain models for the eccentricity and apsidal angle of planet b. If the orbits are aligned, then the true model needs to fall within the red dotted lines, which mark the position of the (much better determined) apsidal line for planet c. From looking at the figure, the apsidally aligned configurations seem to have e_b ~ 0.01±0.005.

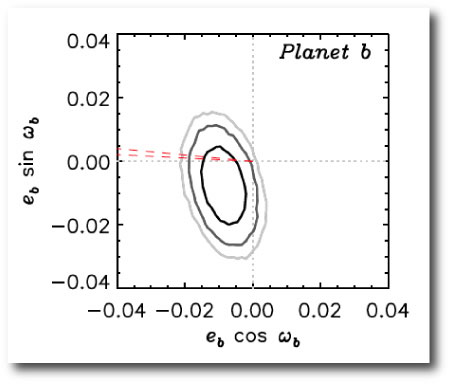
I asked Josh if he could send a histogram that shows the distribution of eccentricities for planet b for the subset of models that satisfy the alignment criterion. He got back to me very quickly with the following plot:

The result is: e_b = 0.0106 ± 0.0040, which implies a best-guess planetary structure that has (1) a small core, (2) a Love number k_2~0.34, and (3) a tidal dissipation quality factor Q~10,000 (see our paper, Batygin, Bodenheimer & Laughlin 2009 for details).

HAT-P-13c could easily wind up being 2010’s version of HD 80606b — a long-shot transit candidate that pans out to enable extraordinary follow-up characterization, while simultaneously allowing small-telescope ground-based observers to stunt on the transit-hunting space missions.

The HAT-P-13 system has already gotten quite a bit of oklo.org press (see articles [1], [2], and [3]). It generates intense interest because it’s the only known configuration where a transiting short-period planet is accompanied by a long-period companion planet on an orbit that’s reasonably well characterized by radial velocity measurements. Right after the system was discovered, we showed that if the orbits of the two planets are coplanar, then one can probe the interior structure of the transiting inner planet by getting a precise measurement of its orbital eccentricity. The idea is that the system has tidally evolved to an eccentricity fixed point, in which the apsidal lines of the two planets precess at the same rate. Both the precession rate and the inner planet’s eccentricity are single-valued functions of the degree of mass concentration within the transiting planet.

Early this year, Rosemary Mardling expanded the analysis to the situation where the two planets are not orbiting in the same plane (her paper here). If there is significant non-coplanarity, the system will have settled into a limit cycle, in which the eccentricity of the inner planet and the alignment angle of the apsidal lines cycle through a smoothly varying sequence of values. The existence of a limit cycle screws up the possibility of making a precise statement about planet’s b’s interior, even if one has an accurate measurement of the eccentricity.

When one ties all the lines of argument together, it turns out that there are two different system configurations that satisfy all the current constraints. In one, the planetary trajectories are nearly co-planar, with the inclination angle between the two orbits being less than 10 degrees. If the system has this set-up, then we’ll be in good position to x-ray the inner planet. In the alternative configuration, the orbital planes have a relative inclination of ~45 degrees, and the limit cycle will hold.

Matthew Payne, a postdoc at Florida, along with Eric Ford, have done a detailed examination of the transit timing variations that the two configurations will produce. (Transit timing variations — or TTV as all the hipsters were referring to them last week at SXSW — have been all the rage during the last few years, but have so far generated more buzz than results. That should change when HAT-P-13 takes the stage.) Payne and Ford found that timing variations should amount to tens of seconds near the periastron of planet c, which should in turn allow a resolution of whether the system is co-planar or not:

HAT-P-13 is a tough system for small-telescope observers to reach milli-magnitude precision at a cadence high enough to accurately measure the transit timing variations. Nevertheless, the top backyard aces will be giving it a go. Bruce Gary has reactivated the AXA especially for the event, and University of Florida grad student Ben Nelson has written a campaign page for Lubos Brat’s Tresca database. The best transits for detecting TTV will be occurring during April and May. This is an opportunity to really push the envelope.

If the system turns out to be close to coplanar, then there’s a non-negligible probability (of order 5-10%) that planet c will be observable in transit. The transit window is centered on April 12th, and is uncertain by a few days to either side. Small telescope observers will definitely be competitive in checking for the transit. In an upcoming post, we’ll take a look at the details and the peculiarities of this remarkable opportunity.