The long-term stability of the planetary orbits has been a marquee-level question in astronomy for more than three centuries. Newton saw the ordered structure of the solar system as proof positive of a benign deity. In the late 1700s, the apparent clockwork regularity of interaction between Jupiter and Saturn helped to establish the long-standing concept of Laplacian determinism. In the late Nineteenth Century, Poincaré’s work on orbital dynamics provided the first major results in the study of chaotic systems and nonlinear dynamics, and began the tilt of the scientific worldview away from determinism and toward a probabalistic interpretation.

In the past ten years, it has become fairly clear that the Solar System is dynamically unstable, in the sense that if one waits long enough (and ignores drastic overall changes such as those wrought by the Sun’s evolution or by close encounters with passing stars) the planets will eventually find themselves on crossing orbits, leading to close encounters, ejections and collisions. The question has shifted more to the following: What (if any) chance is there that the planets will experience orbit crossings within the next 5 billion years?

It’s clear that the probability of the planets going haywire prior to the Sun’s red giant phase is pretty small. Computers are now fast enough to integrate the eight planets forward for time scales of ten billion years or more. Konstantin Batygin, a UCSC physics undergrad who has been collaborating with me, has been running a suite of very long term solar system integrations, and he’s been getting some nice results.

It’s well known that over the long term, the planetary orbits are chaotic. The Lyapunov timescales for the planetary orbits in both the inner and the outer solar system are of order a few million years, which means that for durations longer than ~50 Myr into the future, it becomes impossible to make a deterministic prediction for exactly where the planets will be. . We have no idea whether January 1, 100,000,000 AD will occur in the winter or in the summer. We can’t even say with complete certainty that Earth will be orbiting the Sun at all on that date.

We can, however, carry out numerical integrations of the planetary motions. If the integration is carried out to sufficient numerical accuracy, and starts with the current orbital configuration of the planets, then we have a possible future trajectory for the solar system. An ensemble of integrations, in which each instance is carried out with an unobservably tiny perturbation to the initial conditions, can give a statistical distribution of possible long-term outcomes.

Here’s a time series showing the variation in Earth’s eccentricity during a 20 billion year integration. In this simulation, the Earth experiences a seemingly endless series of secular variations between e=0 and e=0.07 (with a very slight change in behavior at a time about 10 billion years from now). The boring, mildly chaotic variations in Earth’s orbit are mostly dictated by interactions with Venus.

Mercury, on the other hand, is a little more high-strung.

These two plots suggest that the Solar System is “good to go” for the foreseeable future. Indeed, work by Norm Murray and Matt Holman suggests that the four outer planets have a dynamical lifetime of order one hundred quadrillion years. Work by Jaques Laskar, however, suggests that the inner solar system might be on far less stable footing. Konstantin has obtained some very interesting new results on this particular point, which we’ll be sharing in an upcoming post…

Image Source.

Galileo’s discovery of the four major Jovian satellites — his Medicean Stars — revealed that Jupiter is accompanied by a planetary system in miniature. In his Dialogue on the Two Chief World Systems, Galileo drew on the obvious analogy between Jupiter and its moons on the one hand and the Sun and the planets on the other as evidence in favor of the Copernican worldview.

The pattern is that when an orbit is larger, the revolution is completed in a longer period of time; and when smaller, in a shorter period. Thus Saturn, which traces a greater circle than any other planet, completes it in thirty years; Mars in two; the moon goes through its much smaller orbit in just a month; and in regard to the Medicean stars, we see no less sensibly that the one nearest Jupiter completes its revolution in a very short time (namely about forty-two hours), the next one in three and one-half days, the third one in seven days, and the most remote one in sixteen. This very harmonious pattern is not changed in the least as long as the motion of twenty four hours is attributed to the terrestrial globe (rotating on itself).

Image Source.

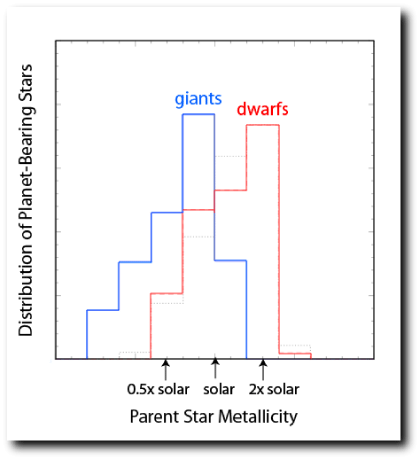
Two decades ago, prior to the discovery of the extrasolar planets, the Galilean satellites, along with the regular satellite systems of Saturn and Uranus, constituted one of the strongest hints that extrasolar planets should exist. In each case, the total fractional mass and relative orbital scale of the satellites is quite similar, implying that a robust and generic formation process was at work. There’s a factor-of-twenty difference between the masses of Jupiter and Uranus, but the fractional mass caught up in their satellites differs by only a factor of two. The Jovian satellites add up to 0.021% of Jupiter’s mass, whereas the Uranian moons amount to 0.011% of Uranus’ mass. Similarly, the Saturnian satellite system (which is completely dominated by Titan) has a total mass amounting to 0.025% of Saturn. In all three cases, the orbital distance of the outermost large satellite is between 20 and 60 planetary radii.

Robin Canup and Bill Ward of Boulder’s Southwest Research Institute have developed a compelling formation model that naturally accounts for the similarities between the giant planet satellite systems (see here and here). In their picture, regular satellites build up from solid particles that flow into the circumplanetary disks from the surrounding solar nebula. Once a nascent moon reaches a non-trivial size, it decouples from the inward spiral of gas, and is able to rapidly accrete large quantities of solid particles. Ultimately, a satellite’s ability to grow to very large size is shuttered by Type I migration, whose timescale decreases in inverse proportion to the satellite mass. In the Canup-Ward picture, a succession of Jovian satellites form and are accreted onto the central planet when their mass exceeds ~0.02% of the planetary mass.

The flow pattern in the outer region of a protoplanet’s Roche lobe that regulates the flow of gas into the circumplanetary disk is quite complicated. Here’s an image adapted from the hydrodynamical simulations of Steve Lubow and his collaborators (paper here) that shows the streamlines in the vicinity of the forming planet’s Roche lobe:

The gravity of the Sun produces a tidal barrier which meters the flow of gas into the protoplanetary disk, and Canup and Ward compare the Jovian satellites to the buildup of mineral deposits on the interior of a pipe through which a great deal of water has flowed.

Squeezing out regular oklo posts is a bit of a challenge. I want to keep the posting schedule fairly regular in order to keep the readership up, but at the same time, its sometimes hard to keep coming up with post-worthy topics. In trolling for ideas, I often go to the Extrasolar Planets Encyclopaedia and comb through the tables, looking for patterns or analogies. A bit more than a year ago, I noticed that Gl 876 d, with its 1.92-day orbit and its 0.007% mass ratio is reminiscent of a Jovian satellite. Could it have arisen from a direct analog of the Canup-Ward formation process?

In the Gl 876 system, the middle planet c would have metered the gas flow into Gl 876’s inner circumstellar disk. A considerable amount of the inward flowing gas in the nascent Gl 876 system would have accreted onto planet c, but there was likely a stream (or streams, given the additional presence of planet b) that bypassed the planets and flowed onto the inner disk. The low density of steadily flowing gas in the inner disk would have allowed planet d to feed on the incoming solid material while staving off demise via Type I migration. The formation of d through this process would have occurred entirely within the Gl 876 snowline, and so in this picture, planet d is composed largely of iron and silicates. Figure 10 from the Lubow et al. paper gives a nice sense of how gas and small solid particles would have slipped by planet c on their way in:

Willy Kley and his collaborators have done hydrodynamical simulations which model the interaction between that the outer two Gl 876 planets and the parent gas disk. The flow pattern in the vicinity of the planets is more complicated than in the single-planet case, and streams of gas (and small particles) are able to flow into the disk region interior to the 30-day orbit of planet c. It’s not unreasonable to imagine that the combined presence of planets b and c mediated an inner circumstellar disk around GJ 876 that was reminiscent of the circumplanetary disk around a Jovian planet. Here’s an example figure from the Kley et al. paper showing the hydrodynamical flow in the vicinity of planets b and c:

It thus seems plausible that GJ 876 d could indeed owe its origin to the same process that produced the Jovian satellites. The planet d that shows up in the radial velocity data might be the largest survivor among a number of similar iron-silicate planets that formed in the gas-starved inner disk and were then lost to the star via type I migration. In keeping with the analogy to Jovian satellites, this scenario would hint at additional, somewhat smaller iron-silicate planets circling Gl 876 in orbits with periods in the 4-12 day range. Looks like more RVs are in order!

A manufacturing scheme akin to the giant planet satellite formation process is, however, not the only way to produce Gl 876 d. Doug Lin and his collaborators, for example, have suggested that GJ 876 d formed from pre-existing icy planetesimals that were herded inward during the resonant migration of the massive outer planets b and c. In their picture, Gl 876 d is made largely from water, and would thus have a larger physical radius than if it was built primarily from silicates via a Jovian satellite-like formation process. Mandell et al. outline a related mechanism by which d could have formed via resonant shepherding.

It’s a shame that d doesn’t transit.

Are there any other inner planets that might be candidates for formation via the Canup-Ward mechanism? Plausible clues would consist of a short orbital period, a ~0.01% mass ratio, and a massive outer planet in a ~10-50 day orbit. 55 Cancri e just might fit that bill…

Image Source.

Mike Valdez pointed me to an interesting paper by Pasquini et al. that was posted to astro-ph today. The authors examined the frequency with which Jovian-mass planets are detected around giant stars and dwarf (that is, ordinary main sequence) stars as a function of the metallicity of the host star. Their main result is summed up in this redrawn figure:

The red histogram shows the well-known result that detectable Jovian-mass planets are preferentially found around metal-rich stars. The blue histogram shows a result that seems surprising at first glance. It indicates that for giant stars, the metallicity effect essentially goes away. The distribution in the blue histogram is not much different from the overall distribution of stellar metallicities in our local galactic neighborhood.

Pasquini et al. give several possible explanations for their result. Their favored interpretation is that the planet-metallicity correlation is due not to high intrinsic metallicity, but rather to stellar pollution. The idea is that after a planet-bearing star forms, its thin convective envelope is enriched by the accretion of heavy elements. The planet-bearing stars that have metal-rich spectra are in actuality ordinary stars sheathed in enriched envelopes. As polluted stars evolve off the main sequence, their convective envelopes grow deeper, and the apparent metallicity enhancements largely disappear.

As an inveterate adherent of the core-accretion hypothesis for the bulk of giant planet formation, my knee-jerk reaction is to be unhappy with a pollution interpretation. Disks and (by extension) stars that are metal-rich are more capable of building planetary cores while there’s still gas remaining in the protoplanetary disk. The planet-metallicity connection is thus a natural consequence of the core accretion hypothesis.

Pasquini et al. point out that the giant stars in their sample are systematically more massive than the main-sequence stars for which the planet-metallicity connection has been established. This leads them to speculate:

Since the fraction of planet-hosting giants is basically independent of metallicity, it is feasible that intermediate mass stars favor a planet formation mechanism, such as gravitational instability, which is independent of metallicity. One could speculate that such a mechanism is more efficient in more massive stars, which (likely) have more massive disks.

I don’t completely agree with this interpretation either, but I do think that the correct explanation is tied into a systematic difference in stellar mass between the giant sample and the dwarf sample. While it’s somewhat difficult to get accurate masses for giants, its reasonable to assume that the average mass of the giants in the above histogram is ~2 solar masses. If we assume that protostellar disks scale in mass with the mass of the parent star, then the average disk around a 2 solar mass star had roughly twice the surface density of solids than the average disk around a solar mass star. This is equivalent to a 0.3 dex increase in metallicity in a disk around a solar mass star, neatly explaining the magnitude of the offset between the red and the blue histograms.

The paucity of planets around high-metallicity giants probably stems in part from small number statistics and from the fact that there are very few super-metal-rich giants in the survey. Note that the histograms plot the distributions in metallicity for planet-bearing stars, and not the fraction of planet-bearing stars in a complete sample as a function of metallicity Although a detailed Monte-Carlo experiment is definitely in order, I think that Pasquini et al.’s result will end up being fully in line with the expectations of the core-accretion theory.

This argument would have had a lot more weight if I’d done a detailed Monte-Carlo analysis in advance, rather than monday-morning-armchair-quarterbacking (that is, blogging) with a smug postdiction. I think, however, that the core-accretion theory indicates that these general trends will all continue to hold true:

Image Source.

Last weekend, I participated in the “Future of Intelligence in the Cosmos” workshop at NASA Ames. In an age of ultra-specialized conferences, the focus for this one bucked the trend by pulling back for the really big picture:

The Future of Intelligence in the Cosmos” is an interdisciplinary two-day workshop that seeks to elucidate potential scenarios for the evolution of intelligent civilizations in our galaxy and thus, perhaps, to find a resolution for this seeming paradox. The probability that intelligent civilizations exist has been succinctly stated by the Drake Equation. While the first few terms in the equation, such as the number of stars in the Milky Way Galaxy, the fraction of stars that have planets, and the number of planets in the habitable zone, are becoming better known, the last three terms that depict the fraction of planets that evolve intelligent life, the fraction that communicate, and the fraction of the lifetime of the Milky Way Galaxy over which they communicate, are not well known. It is these last three terms in the Drake Equation that are the focus of the workshop.

In most venues, extrasolar planets veer toward the esoteric. At this workshop, however, the galactic planetary census was perhaps the most nuts-and-bolts topic on the agenda. We know that planet formation is common in the galaxy, and its increasingly clear that the “great silence” isn’t stemming from a lack of Earth-mass worlds.

Here’s a link to a .pdf document containing the slides from my talk.

In an upcoming post, I’ll try to pull together a synopsis of what emerged from the conference. Perhaps the most startling moment for me came in Paul Davies‘ talk, when he described the extent to which the simulation argument has been developed.

When I was in graduate school, Frank Drake was a faculty member in our Department. I noticed right away that the license plate on his car read “neqlsl”. I always read this as “n equals one”, until I finally asked him which term was responsible for thwarting all the alien civilizations.

“It’s not N equals one,” he said, “it’s N equals L”.