
Image Source.
First, I squandered literally years of opportunity to coordinate a photometric follow-up transit search on Gl 436. Then I managed to incorrectly report the circumstances of the detection on the initial version of this (now corrected) oklo post! Naturally, I’m feeling sheepish, and my situation bears a distant echo to that of John Herschel (son of William), who was partly to blame for the inadequate coordination of an observational follow-up to John Couch Adams’ predictions of Neptune’s location.
Following the stunning news from the Continent of LeVerrier’s prediction and Galle’s successful detection of Neptune, Herschel likely realized at once that Neptune’s discovery would have gone to England had only he pressed Adams’ case more assiduously. In an October 1, 1846 letter to the London Athenaeum, Herschel hems and haws in a somewhat disingenuous effort to wriggle out of the uncomfortable situation that he had put himself in.
“The remarkable calculations of M. Le Verrier – which have pointed out, as now appears, nearly the true situation of the new planet, by resolving the inverse problem of the perturbations – if uncorroborated by repetition of the numerical calculations by another hand, or by independent investigation from another quarter, would hardly justify so strong an assurance as that conveyed by my expression above alluded to. But it was known to me, at that time, (I will take the liberty to cite the Astronomer Royal as my authority) that a similar investigation had been independently entered into, and a conclusion as to the situation of the new planet very nearly coincident with M. Le Verrier’s arrived at (in entire ignorance of his conclusions), by a young Cambridge mathematician, Mr. Adams; – who will, I hope, pardon this mention of his name.”
Herschel also wrote urgently to his friend William Lassell, a wealthy beer brewer from Liverpool, and a skilled observer who owned a fine 24-inch reflector. Herschel exhorted him to partially salvage the situation for himself and for Britain through a search for “satellites with all possible expedition!!”
Lassell began observing Neptune immediately, and within a week had spotted what was later confirmed to be Neptune’s satellite Triton. This, however, did little to assuage the court of British public opinion, and Challis, Airy, and Herschel were savaged for their inaction. “Oh, curse their narcotic Souls!” wrote Adam Sedgwick, professor of Geology at Trinity College.
[I culled these anecdotes from my favorite book on the topic of Neptune, Vulcan, LeVerrier and 19th-century dynamical astronomy; “In Search of Planet Vulcan — The Ghost in Newton’s Clockwork Universe” by Richard Baum and William Sheehan.]
Unfortunately, even with the exertion of all possible expedition, the detection of satellites orbiting Gl 436 b is a long shot. Large moons orbiting a planet only 0.02 AU from the parent star are almost certainly dynamically unstable (as shown here), and would, in any case, require exquisite photometry to detect. But one can, however, investigate the possibility that Gl 436 b might point the way toward other detectable planets in the system.
The first clue that Gl 436 might harbor more than one planet comes from planet b’s considerable, e~0.16, eccentricity. It’s surprising to find a P=2.644 day planet on a non-circular orbit. Given that its tidal quality factor, Q, is likely similar to Neptune’s, it should have circularized a long time ago — unless there’s a source of ongoing gravitational perturbation.
Gl 436 b’s high eccentricity means that, like Jupiter’s moon Io, it’s experiencing a lot of tidal heating. It’s internal luminosity is likely of order 10^20 Watts, which is in the rough ballpark of the amount of energy that the planet intercepts from the red dwarf parent star. Another interesting consequence of the non-zero eccentricity is that b will have a pseudo-synchronous spin period. That is, tidal forces will have forced the planet into a rotational period of 2.29 days, which allows it to optimally show one face to the star during periastron passage when the tidal forces are strongest. Jonathan Langton has done a simulation of the surface flow pattern (assuming a water-vapor atmosphere). The following 1.1MB animations (“eastern” view, and “western” view) trace two full orbits in the planet’s frame, and show the slow synodic drift of the baking daylit hemisphere.
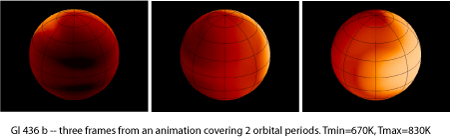
If there’s a perturbing companion to Gl 436 b, then it’s a reasonable guess that it lies in roughly the same orbital plane, meaning that there’s a non-negligible chance of transit. It would certainly be nice if such a transit could be predicted in advance…
The first task is to look at whether the published radial velocity data set for Gl 436 gives any hint of additional planets. Going to the “Real Star” catalog on the systemic backend, and calling up the “gj436_M07K” dataset shows a wide variety of fits that have been submitted by systemic users over the past nine months:
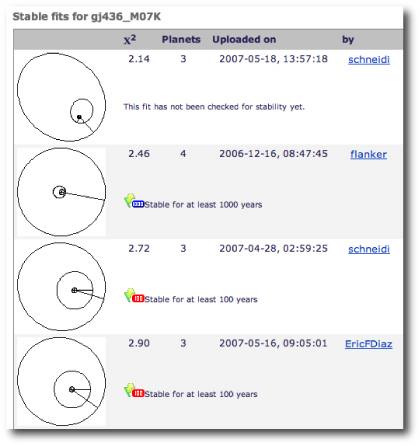
Unlike the case of Gl 581c, there’s no particularly compelling evidence for a second planet. In sifting through the various fits that have been submitted, one finds that a second planet with a mass similar to Uranus and a period of 53 days is probably the most likely candidate perturber, and using the console, I find an unpublishably high false-alarm probability of 49% for a planet “c” with these properties. (The discussion boards on the systemic backend indicate that the systemic users have also arrived at this conclusion.)
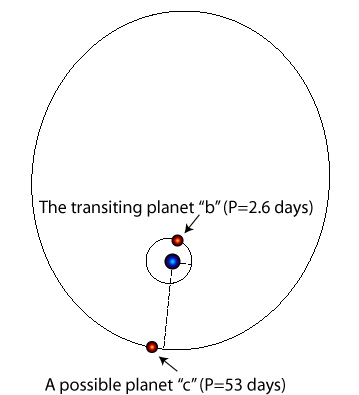
On the other hand, however, a coin-flip isn’t half-bad odds, and what better low-stakes venue than a blog for an analysis? Let’s go ahead and assume that the 53-day candidate is really there.
At the current time, the console software isn’t configured to incorporate transit information into radial velocity fits. In particular, when one has a transit, one gets (1) an excellent determination of the period, and (2) an accurate ephemeris of the moment when the transiting planet and the parent star both lie on the line of sight to the Earth. Condition (2) provides a constraint on the fit that replaces the transiting planet’s Mean Anomaly as a free parameter. I have a Fortran code (that I wrote for an analysis of the orbit of HD 209458b) that handles this situation, and so I can carry out a self-consistent two-planet fit that takes advantage of the transit ephemeris for b reported in the Gillon et al. paper. This 2-planet fit (based on the 53-day Uranus suggested by the fits submitted to the systemic backend) has a chi-square statistic of 3.09, and an RMS scatter of 3.91 m/s. The orbital parameters of the planets are: P_b=2.64385d, P_c=53.57724d, e_b=0.1375, e_c=0.2281, omega_b= 347.999 deg, omega_c=185.146 deg, M_b=0.0697 M_jup, and M_c=0.0417 M_jup. The Mean Anomaly of the putative planet “c” at JD 2451552.077 is 100.69 degrees.
One would certainly prefer to see a beefier perturber for Gl 436 b. When I compute the Laplace-Lagrange 2nd-order secular theory for the above system (including the effects of general relativistic precession) I find that b’s eccentricity cycles between e_min=0.135 and e_max=0.160 with a period of 13,000 years. This is much shorter than the time scale for orbital circularization, but it’s not immediately clear to me whether the secular perturbations from c would be able to maintain such a large eccentricity for b over billions of years. Does anyone know the answer offhand? That is, if b and c both formed with sizable eccentricities, would the secular interaction prevent circularization by providing c with a mechanism to offload angular momentum?
In any case, if c is for real, and if its orbital plane is properly aligned for central transits, then they will occur on (all times UT):
ingress JD: 2454152.02 2007, Feb 20, 12:34
egress JD: 2454152.19 2007, Feb 20, 16:29
ingress JD: 2454205.60 2007, April 15, 2:24
egress JD: 2454205.77 2007, April 15, 6:24
ingress JD: 2454259.18 2007, June 7, 16:14
egress JD: 2454259.34 2007, June 7, 20:14
ingress JD: 2454312.75 2007, July 31 06:04
egress JD: 2454312.92 2007, July 31 10:04
I’m now doing a more detailed analysis to see if c can maintain the observed eccentricity of b over the long term. If it’s a go, then I’ll run a bootstrap calculation to determine the probable error on the above predictions. It might be useful, however, to mark down June 6th-8th on the calendar.

That’s an intriguing, Greg, i.e. “if b and c both formed with sizable eccentricities, would the secular interaction prevent circularization by providing c with a mechanism to offload angular momentum?”. It is a question over which I have pondered, but as with you, one to which the answer has eluded me. But, I will continue my work on Gl 436, going under the assumption that Gl 436c, with a period of ~53 days, is real. Hopefully, our colleagues from tansitsearch.org can shed more light (pardon the pun) on this problematic system with their observations.
Eric
Hi Eric,
It seems to me that the problem can be investigated numerically using a “double averaging” approach to the evolution. One can use the secular theory to advance the system forward over a secular timestep of hundreds to thousands of years. After each secular timestep, one can apply tidal dissipation (modify semi-major axis and eccentricity so as to decrease the energy of planet b while conserving its angular momentum). Then take another secular timestep, etc. This seems a reasonable approach so long as the secular time scale is much shorter than the tidal evolution time scale, which does appear to be the case.
Greg
Hi Greg,
That makes perfect sense and does seem like a reasonable approach the way you have explained it. It is also an encouraging bit of information. Thanks for explaining it to me, Greg. I’ll let my colleagues know about this blog.
Best regards,
Eric
Greg-
To answer the eccentricity damping question, I would refer to the two papers you and Fred Adams put out last year. I don’t recall the specifics, but maybe the formulae you developed there aren’t applicable to this situation.
Other good work on this problem has been done by Ke Zhang and his advisor Doug Hamilton. You can look here (http://www.astro.umd.edu/~kzh/research.html) for an overview, although the main paper hasn’t been published yet. He actually solves the problem analytically and places useful constraints on the outer planet’s orbital elements (apsides aligned or anti-aligned, semi-major axis/eccentricity/mass relations) for fitting to RV curves.
Another possiblity is a resonant configuration (which is probably even harder to find in the RV data). As I understand it, in resonance the angular momentum transfer process is very efficient, so the resonance is maintained even if one of the planets is drifting. I don’t have a good feel for eccentricity variations in these systems though. The work on Jovian and Saturnian moon systems is sort of relevant, but the ratio of tidal parameters for a star/planet is much closer to 1 than gas planet / terrestrial moon.
A related question. In some past posts, we’ve noticed some eccentric close-in planets where it seems clear that there is no massive perturber. One theory for these systems is that (due to fast rotation), the tidal parameters are such that eccentricity is pumped, rather than damped. This was explored in Dobbs-Dixon et al. (http://adsabs.harvard.edu/abs/2004ApJ…610..464D)
but I’m not sure if it’s been photometrically verified: is there a correlation between stellar spin period and warm Jupiter eccentricity? So, it’s not impossible to form an eccentric system with only 1 planet. Or sometimes (80606), the eccentricity is induced by a very distant (stellar) perturber on a highly-inclined orbit.
It’s exciting (for me) that dynamics can give us a strong insight into these system and guide the RV fitting. Unfortuneately, most dynamical mechanisms requiring two planets also would predict a relative inclination of several degrees, so the second planet may not transit. Such a system would still be really interesting and a new discovery as there are no transiting planets with other known additional planets, if I recall correctly.
Darin
Hi Darin,
[I’m back from class and am updating this comment.]
The analytic solutions 2.2 of the AL paper assume that the eccentricity of the inner planet goes through zero during the course of a secular cycle, so I’m going to use the double averaging approach to do the time integration of a and e.
As for the stellar rotation, I don’t think any of the well-characterized hot Jupiters have parent stars that are rotating fast enough to cause eccentricity pumping for the planet. This is partly due to a selection effect: rapid rotators give bad RV precision, and these stars are generally dropped immediately from the surveys.
best,
G
Hi Darin,
I read your comment on my personal page. Just so you know, I’ve already tried mean-motion resonance (i.e. 3:1,4:1 and 5:1) and in each case the mass of the perturbing body was less than that of Gl 436b. If you try to impose a higher mass on a shorter period planet then, what invariably happens is that the Chi² value becomes inordinately high.
As far as the Kozai mechanism of HD80606, since Gl 436 does not have a stellar companion, I tried something rather unique and unorthodox. I thought perhaps if there were a slow moving, supermassive brown-dwarf with a very long orbital period in the data orbiting Gl 436, then that would an effect create a kind of quasi-Kozai effect. But, again the mass simply wasn’t enough to account for the .16 eccentricity of Gl 436b. In point of fact the very long period planet didn’t even have 1.0 MJup; it was around .92 if I recall correctly.
And, as Greg pointed out, rapidly rotating stars are excluded because the greater the Doppler shift the more obscured the spectral lines become as they are widened by the rapid rotation. I’ve seen digital spectrographs of rapidly rotating stars and they are a mess. So, that’s not an option.
I’ve been doing some reading on the usefulness of secular theory in the cases of small planets and/or highly eccentric orbits. And, what I’ve read seems to concur with what Greg has said about using a double averaging approach as being the most reasonable way to approach this particular problem.
Believe me when I say that I have exhausted just about every other possibility, and the only approach left that makes any sense at all to me at this point, is the one delineated by Greg.
Best regards,
Eric
Eric-
Glad to hear my comments have been somewhat useful. I think the double averaging technique will work well for this system. Zhang & Hamilton may be able to guide the initial parameters as well. (Interestingly, your best fit has the two planets anti-aligned, which they would predict.) I agree that rapid rotators are generally unlikely and for transiting planets (i.e. 436b), short rotation periods would have probably been seen in the photometry. So, barring some unusual tidal parameters, eccentricity pumping is unlikely.
The Kozai mechanism involves a distant massive companion on a *highly inclined* orbit. Since the console doesn’t do inclinations, it can’t truly simulate the Kozai effect. If the relative inclination between the planet and a distant massive perturber is greater than about 60 degrees, usually, then the Kozai mechanism allows for angular momentum exchange between the planet’s eccentricity and its (relative) inclination. Sometimes this exchange is extreme (80606). I don’t have a good feel for the masses, etc. necessary to cause the Kozai mechanism, but I feel like it would be hard to detect the distant planet in the RV data. (Or, maybe your ~Jupiter mass planet is highly inclined with respect to the line of sight and so its true mass is large enough.) However, this is a nearby well-studied star with no indication of binarity.
Eric, just because your resonance fits don’t have a more massive exterior planet doesn’t mean they aren’t worth considering. Anything that has a nice chi-squared (and good F-test) is worth looking at. Our goal should be to take any good fits and use dynamics and ask, “can this fit explain how 436b has maintained a large eccentricity despite tides?” Or, more subtly, is there a reasonable fit that doesn’t give 436b a large eccentricity, thereby obviating the problem. We then take whatever solution we come up with and search for transits.
In any case, I wish I could do more than just provide random comments. Whatever the outcome, it’s quite interesting.
Darin
Hi Darin, Eric,
Thanks for the discussion. It’s exciting to see systemic operating as intended as a framework for collaboration.
Regarding inclination, the console has full three-d capability under the hood, and indeed, one of Aaron’s earlier versions had node and inclination sliders. We decided early on to pull that functionality from the distribution version. Up until now, GJ 876 was the only data set that contains enough interaction to warrant inclusion of inclination, and even for GJ 876, it’s really only useful to look at chi^2 as a function of co-planar inclination.
Stefano has, however, just implemented transit timing constraints into the next version of the console. The S/N of a transit midpoint observation is far higher than the S/N of a radial velocity, and with good transit timing, it’s possible that inclinations from perturbers might be detectable. So we’re looking at rolling out a version which has seven sliders across. (Unpack that 23-inch cinema display)…
Barring that, it might also be useful to supply a special Kozai plugin that would allow the exploration of Kozai interactions while maintaining consistency with the RV data. I’ll bring it up with Eugenio and Stefano at our next code meeting.
best,
Greg
Hi Darin and Greg,
Thanks for all the feedback. I really do enjoy this sort of discourse. Like you said, Darin, it is really interesting.
A special Kozai plugin would really be cool, Greg. And, I think that the transit timing constraints that Stefano has implemented into the next version of the console is a great idea.
Best,
Eric
Greg-
The inclination/node sliders would add complexity, but should be fun for experienced users. I think it would be cool to have a version available with this option. Adding in transits really makes this the sweetest data-fitting program, good enough for professionals.
The fun begins!
Darin
Pingback: systemic - e as in Weird
Pingback: systemic - A hot hot Neptune