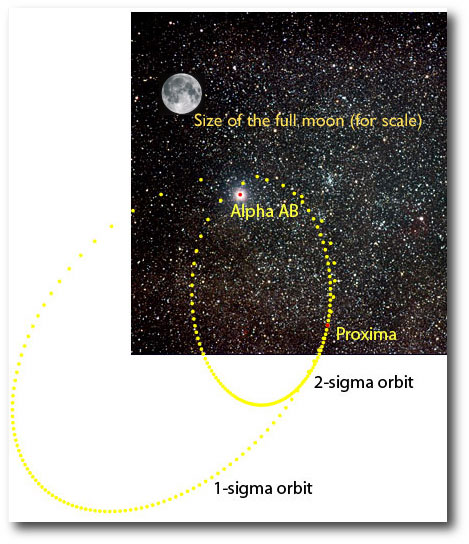
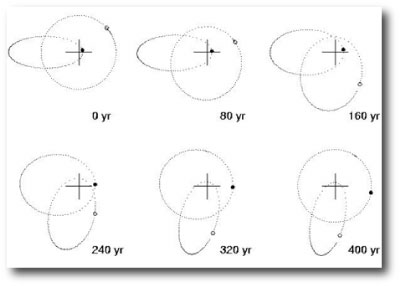
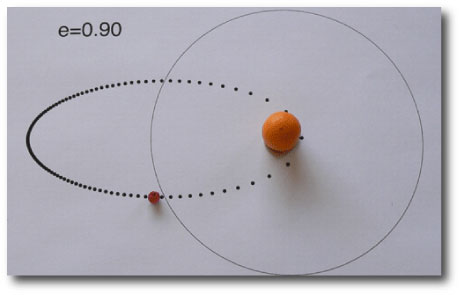
HD 80606 b is one crazy place. With an orbital eccentricity of e=0.932, its orbit resembles a ball tossed almost straight up with a 111.4 day hang time. I’ve heard that in many European countries, periastron passage (when HD 80606 b whips through its closest approach) is known as ‘606 day, and is celebrated by a day off work filled with drunken and disorderly parades. I’m trying to bring the tradition over to the United States.

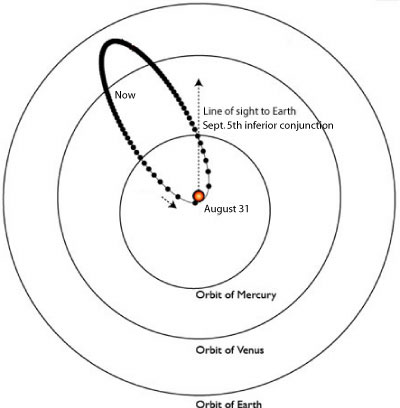
Today (as viewed from Earth) HD 80606 b is just starting to pick up speed on its inward plunge to the next ‘606 day, which occurs on August 31, 2006. The planet has spent the June and July cooling off near the far point of its orbit, at a distance of about 0.85 AU from the central star. It’s possible that weather in the upper atmospheric layers of the planet has spawned a street of category 10 hurricanes that will tear unimpeded around the planet until the steadily mounting insolation turns the driving rains into steam. During the month of August, the planet will fall in almost the full distance to the star, eventually swooping within 6 stellar radii as it whips through periastron.

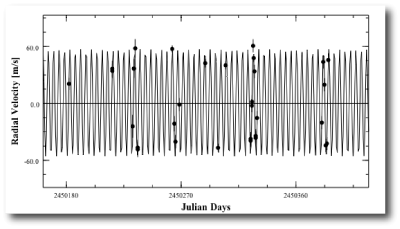
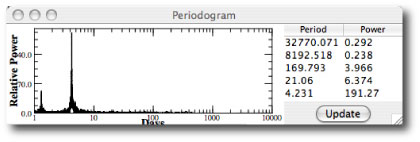
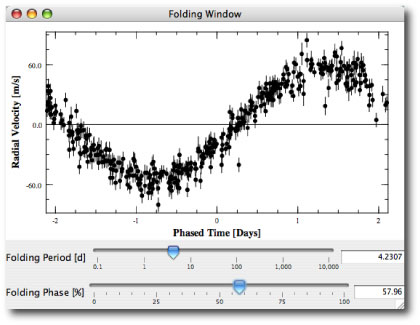
The discovery of the planet and its orbital solution were announced by the Geneva Observatory Planet Search Team in an April 04, 2001 ESO press release, and the radial velocities are available on both the downloadable systemic console and at the CDS repository (see Naef ef al 2001). The recent catalog paper by Butler et al. (see exoplanets.org) tabulates an additional set of 46 high quality velocities for HD 80606. Using the console to get a joint fit to the two datasets gives an updated set of orbital elements: P=111.4298 days, M=3.76 Jupiter masses, and e=0.9321.

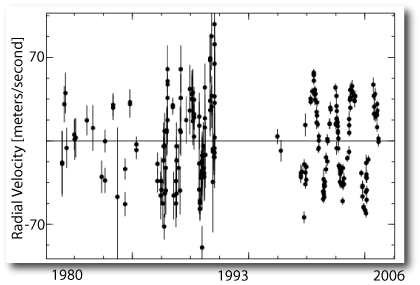
Several years ago, when the California-Carnegie radial velocities for HD 80606 started coming in, Geoff let me have an advance look at them. When I synched the new Keck points up against the Swiss points (which I’d extracted from a published postscript figure) I noticed something interesting. The Keck point obtained on Feb. 2, 2002 was more than 100 m/s above a cluster of Swiss velocities that had been obtained very close to periastron passage.

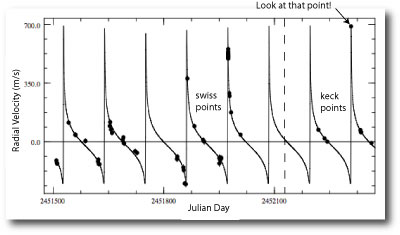
I got excited. The Keck observation suggested that the magnitude of the periastron swing is larger than had been estimated by the published fit. This in turn suggested that the eccentricity of the planet was even larger than the published value of e~0.93. I did an orbital fit and uncertainty analysis on the combined dataset. The best-fit eccentricity came out at a whopping e=0.971 +/- 0.018. An eccentricity this high implied that the planet was regularly swooping to within 2.5 stellar radii of the star. In order for this to be possible, the so-called tidal Q for the planet would have to be very high — higher than the value of around a million that had been inferred from the orbital circularization radii for the hot Jupiters.

In order to confirm the high eccentricity, it would be necessary to obtain more radial velocity measurements in the vicinity of the periastron swing. In June of 2004, I calculated a list of the upcoming periastron dates, and found that one was scheduled for July 11th, 2004 (UT), just a few weeks away. I looked at the schedule for the Keck I telescope, and saw that the California Carnegie team had been assigned a run covering July 8th, 9th, 10th, 11th and 12th. Then I checked where HD 80606 would be located in the Mauna Kea sky. The star was setting rapidly, and was already fairly far to the west at sunset, with and hour angle of more than five hours, and airmass of about three.

I wrote to Geoff and told him about the combined fit that suggested a high eccentricity. Would the star be high enough above the horizon for Keck to observe? He wrote back right away. He was also computing a high value for the eccentricity, and yes, it would be within the limits of observability if the telescope operator was notified in advance.

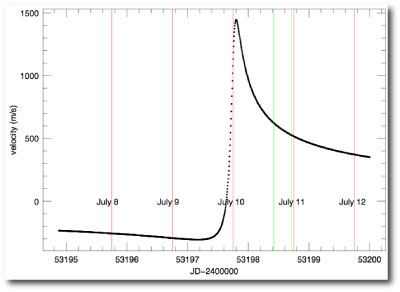
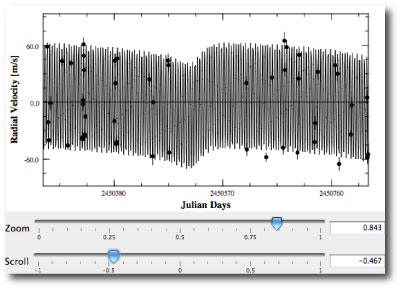
In the plot just above, I’ve reproduced the predicted radial velocity curve during the course of the run. The four vertical red lines show 8:00 PM Keck time on July 8th, 9th, 10th, 11th, and 12th, 2004. Amazingly, the fit suggested that during the brief window of observability on July 10th local time (July 11th UT), the star would be smack in the midst of its most rapid acceleration! The radial velocity fit suggested that a standard six-minute exposure started at 07:30 PM on July 10th would span a reflex velocity change of 60 m/s. By contrast, it takes Jupiter 6 years to indude a 12 m/s velocity change in the Sun.

I waited impatiently through the run, eager to learn what the velocities would be. I kept my fingers crossed that the eccentricity would hold up at e=0.97. Money in the bank. Even if the velocities drove the eccentricity down to its 1-sigma low bound, to e=0.953, it would still be an exciting result, with potentially important consequences for the internal structure of the planet.

On July 10th, at 11 pm PDT (8 pm Hawaii time) I sat at my kitchen table, and imagined the scene on Mauna Kea, with the great dome open to the sky, and Keck I leaning practically on its side, straining to catch the rays of a distant star fading into the last moments of twilight. I thought of the planet itself, stellar furnace filling half the sky, literally jerking the star back into space as it screamed through periastron.

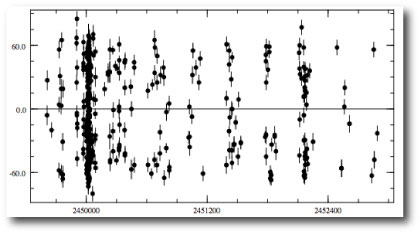
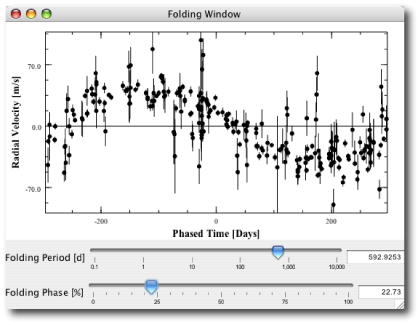
On the morning of the 13th, Geoff sent an e-mail with the velocities. The new fit gave e=0.945. I was stunned. What the @#%? I looked at the velocities themselves, On the 10th, on what was supposed to have been big night, the velocity had failed to rise at all from the value on the 9th. On the 11th, the velocity was only somewhat higher. It was clear that the big swing had occurred several hours afterward. On the 12th, the velocity was high, and clearly past the peak. The planet had arrived at periastron slightly more than a full day later than predicted.

The measured eccentricity was 2-sigma low, an occurrence that one expects less than 2.5% of the time. By chance, the high Keck velocity on Feb. 2, 2002 randomly came within one part in 2000 of arriving exactly at the radial velocity maximum. The fitting program interpreted this high point as suggesting a higher eccentricity than the planet actually has.

I was depressed for the next fifteen minutes. As usual, 95 to 97% of the “cool” discoveries that one turns up in the course of scientific life turn out to be spurious. You have to keep throwing your hat into the ring.

For a theorist, the path of least resistance leads to the abstract. I start to think of planets as signal-to-noise, as peaks on a periodogram. As grant proposals come due, as manuscript drafts bounce back and forth between editors, authors and referees, it’s easy to forget that the planets are really out there, falling endlessly through empty space.

On Monday, we drove up to the Lick Observatory. From the hot rush-hour smog of I-680 in downtown San Jose, the summer-yellow folds of the Diablo range rise out of the hazy valley air. The white telescope domes cling to the highest ridgeline. Exit at Alum Rock. Drive several miles east. The city thins out into suburban sprawl. The Mt. Hamilton Road starts just at the point where the mountains begin to slope up steeply. It takes nearly an hour to cover the 19 miles to the summit, where the observatory buildings sleep mirage-like in the quiet sunlight. Hawks circle against the blue sky. The grasses have dried to straw, and the heat draws the smell of sage and pine resin into the still air.

The dome of the Automated Planet Finder is in place now, and the telescope is nearing completion. It’s visible just to the right of the larger three-meter dome in this photo taken from the main observatory building. The Automated Planet Finder will produce long strings of precise radial velocity measurements. Very soon, we’ll be posting synthetic data sets on the systemic back-end that mimic the observational cadences that this telescope will be capable of providing. It will detect some very interesting planets.

The 36-inch refractor, housed in the great dome of the main building, is still in perfect working order, but it has long since ceded it’s relevance to the cutting-edge. In 1892, E. E. Barnard used it to discover Amalthea, the tiny fifth satellite of Jupiter. This was the last moon in the Solar System to be discovered with the naked eye. More than a century later, the telescope waits silent and unused through most nights. The body of James Lick lies interred at its base. Crickets, lodged in unseen corners of the old building, chirp intermittently in the dark.

Support astronomer Bryant Grigsby brought the great refractor to majestic life. To locate an object on the sky, he repeatedly executed a delicately choreographed sequence of maneuvers. The dome must be rotated so that the slit is positioned on the correct part of the sky. The giant polished and inlaid wood floor must be raised or lowered by up to 16 1/2 feet to bring the eyepiece to eye-level. The 25,000 pound, 57-foot long telescope, perfectly balanced on its pivot, is pulled by hand into rough position, followed by a series of fine adjustments to bring the target into view. The great refractor is priceless. If it’s broken or rendered inoperable, it won’t be replaced. Bryant told me that it took many nights to acquire the confidence to maneuver it on his own.

Just before midnight, he swung the telescope low, nearly to its declination limit, and brought Neptune into view. In the high-power eyepiece, it swam, a dim, very pale, bluish-white circle cut out against matte black. Several star-like points were in the field. One of them may have been Triton. Using Illustrator, I’ve tried to capture how it looked.

What I can’t fully capture, though, is what it is like to stare, for long unhurried minutes, at a giant frigid world on the fringe of our Solar System, with the crickets chirping in warm dry quiet of the dome, illuminated faintly by the glow of a low-watt red bulb and a window open to the distant twinkling lights of the city grid.

Image source.

Last week, I wrote about a plan to send a tiny spacecraft on a trip to the vicinity of Alpha and Proxima Centauri. The idea is to employ a multi-stage rocket to boost a tiny payload toward the stellar system at high speed. When the destination is reached, the principle of gravity de-assist (in the form of successive close flybys of the stars) is used to haul the spacecraft into a bound orbit without using any on-board fuel. [This, of course, is an exercise in orbital dynamics, and not mission proposal. There are better ways to get to Alpha Centauri.]

The problem was tackled by UCSC graduate student Jeremy Wertheimer as his term project for my Astrophysical Dynamics class. Our initial plan was to use a multiparameter minimization scheme (such as the genetic algorithm or simulated annealing) to vary the incoming trajectory of the spacecraft until we found the largest arrival speed that allows for a final bound orbit. To do this requires us to have a precise orbital model for the Alpha AB — Proxima trio.

Amazingly, we discovered that the most recent papers in the literature (from the early 1990s) had arrived at the conclusion that Proxima Centauri is not bound to the Alpha Centauri binary, but rather is in the process of merely drifting past them like a ship in the night. The a-priori odds of Proxima being so close, and so nearly bound, are less than one in a million, but nevertheless, the best position and velocity measurements at that time suggested that this was indeed the case.

In the intervening years since the Matthews & Gilmore 1993 and Anosova et al. 1994 Proxima-Alpha papers were published, there has been a tremendous improvement in our knowledge of the positions, distances, and space velocities of the nearby stars. This improvement is largely due to the European Space Agency’s Hipparcos astrometric satellite, which flew between November 1989 and March 1993 (and whose data was published in June 1997). Hipparcos obtained excellent 3D positional and plane-of-the-sky velocity measurements for both Alpha and Proxima Centauri. When combined with mass and radial velocity measurements for the three stars, the Hipparcos data allows a much better determination of the orbit.

When Jeremy computed an orbit for Proxima using the updated Hipparcos data, he discovered that the measurements now suggest that Proxima Centauri is just barely bound to the Alpha AB pair. He found an enormous elliptical orbit with semi-major axis 272212 AU. (This works out to a whopping 4.3 light years, which is coincidently quite close to the current Sun-Proxima distance.) Clearly, this orbit is much too large, but it’s encouraging to see that the centroid kinematic measurements now indicate that Proxima is formally bound to Alpha.

Even the latest measurements for the Proxima-Alpha Centauri positions and velocities contain uncertainties. In particular, it turns out that the absolute radial velocity for Proxima Centauri has a (still surprisingly large) 1-sigma uncertainty of 200 meters per second. Proxima’s radial velocity in turn has an important effect on whether the three stars are gravitationally bound. Jeremy ran a Monte Carlo simulation in which he drew 10,000 models of the Proxima-Alpha system parameters from the Gaussian distributions implied by the uncertainties in the observations. When he plots the binding energy of these models against the value for Proxima’s radial velocity, he finds that 44% of the trial systems are bound (that is have total energy = gravitational energy + kinetic energy less than zero).

Many of the bound trial systems have energies very close to zero, and hence place Proxima in absurdly large orbits around Alpha. In these configurations, Proxima is currently at the periastron (that is, the near-point) of its orbit. An object in a highly eccentric orbit, on the other hand, spends most of its time near apastron (the orbital far-point).

To illustrate how objects tend to spend their time near apastron, here’s a home-made mpeg-4 stop-action animation of a peppercorn orbiting a kumquat in an ellipse with e=0.90. (Try this version if the other one loads a screen of gibberish).

.

If Proxima is indeed bound to Alpha, then we would (a-priori) expect to find it near apastron. In the figure above, the Monte-Carlo generated orbits in which Proxima is close to apastron have been marked with stars. These orbits all fall in the part of the graph where Proxima’s radial velocity is in the vicinity of -22.1 kilometers per second. We thus have a prediction: if Proxima’s radial velocity is measured to high accuracy, then the value will be ~-22.1 kilometers per second, rather than the current value of ~-21.8 kilometers per second.

In the figure below, I’ve plotted two of the Monte-Carlo orbits for Proxima with respect to Alpha. The “two sigma” orbit is an example of a realization in which Proxima is slightly closer to apastron than periastron. The orbits are projected onto the plane of the sky, and superimposed on an actual photograph of Centaurus (with the full Moon digitally superimposed to give a sense of scale). If our analysis is correct, it should take Proxima about a million years to make one orbit of Alpha, and the semi-major axis of the orbit should be about 1/6th of a light year: