Tag Archives: Gliese 581

Red Dwarf Metallicities

Posted on by
11

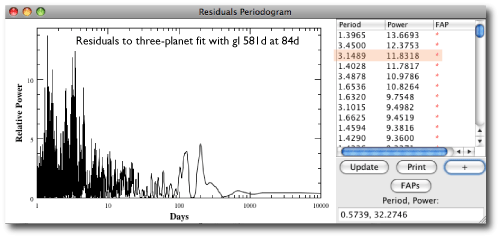
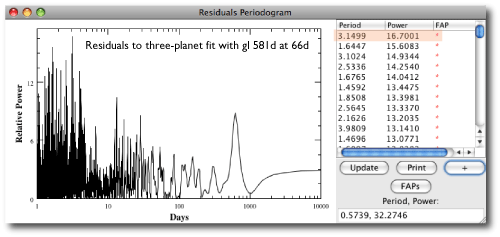
A core prediction of the core accretion model for giant planet formation is that the frequency of readily detectable giant planets should increase with both increasing stellar metallicity and with increasing stellar mass:

It’s now well established that the above diagram is zeroth-order correct, but until fairly recently, the conventional wisdom held that there is little evidence for a strong planet-metallicity correlation among the handful M-dwarf stars (for example, Gliese 876) that are known to harbor giant planets. One is then naturally led to speculate that the odd giant planets in a systems like Gliese 876 might be the outcome of gravitational instability rather than core accretion.

The profusion of molecular lines in the atmospheres of M dwarfs make it hard to determine their metallicities using the techniques of spectral synthesis that work well for hotter stars like the Sun. Fortunately, though, the red dwarfs’ legendary stinginess provides another opportunity for assessing metallicity. Red dwarfs are so thrifty, and they evolve so slowly, that every single one that’s ever formed has barely touched its store of hydrogen. With all the fuel gauges pegged to full, a critical parameter’s worth of confusion is removed. Red dwarfs of a particular mass should form a well-defined one-parameter sequence in the Hertzsprung Russell diagram, and that parameter should be metallicity. If one can accurately plot a particular low-mass star on a color-magnitude diagram, then there should exist a unique and high-quality mapping to both the star’s mass and its metallicity. Physically, an increase in metallicity leads to a higher photospheric opacity, which provides an effective layer of insulation for a star. Add metals to a red dwarf and it will move down and to the right in the Hertzsprung Russell diagram.

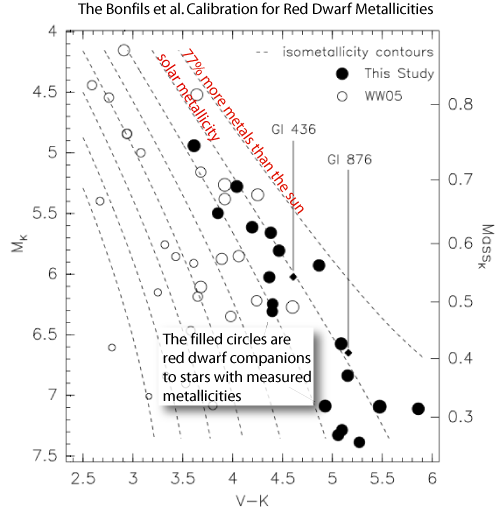
Because of the nightmarish complexity of red dwarf atmospheres, it’s not easy to find the calibration that allows one to make the transformation between an observed absolute magnitude and color index (e.g. M_K and V-K) to the stellar mass and metallicity. In 2005, however, Xavier Bonfils and his collaborators made a breakthrough by employing a simple should’ve-thought-of-that-myself technique: Binary stars generally stem from a common molecular cloud core, and so the members of a binary pair should thus generally have very similar metallicities. In particular, if you measure the metallicity of an F, G, or K binary companion to an M-dwarf, then you can assume that the M-dwarf has the same metallicity. Do this often enough, and you can infer the lines of constant M-dwarf metallicity on a color-magnitude diagram. With the calibration in place, metallicity determinations for field red dwarfs are simply a matter of reading off the nearest iso-metallicity locus. Here’s the key diagram from the Bonfils et al. paper:

The puzzling outcome of the Bonfils et al metallicity calibration was that the rare giant-planet bearing M-dwarfs such as Gliese 876 and Gliese 849 didn’t appear to be particularly metal rich, and that worked to undermine confidence in the core accretion picture. One would naively expect that a low-mass disk will need all the help it can get in order to build giant planet cores before the gas is gone. If anything, the planet-metallicity correlation should be strongest among the M-dwarfs.

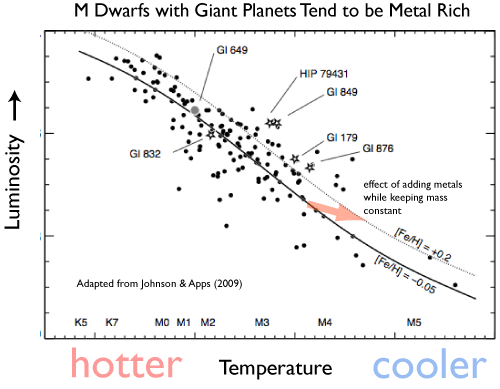
Important recent progress was made last year by John Johnson and Kevin Apps, who published a reevaluation of Bonfil et al’s. isometallicity loci in the color-magnitude diagram. Johnson and Apps point out that application of the Bonfils et al. calibration produces an aggregate of local M-dwarf stars that have a significantly lower average metallicity than that for the local FGK stars. There’s little reason to expect such a dichotomy, which implies that the Bonfils et al. correlation may be systematically underestimating metallicity by roughly a factor of two. No small potatoes!

Johnson and Apps adjusted the calibration to bring the metallicities of the local M dwarfs into line with the metallicities of the local FGK dwarfs. Here’s a slightly adapted version of their key diagram:

With the revised calibration, Gliese 876 turns up with a metallicity twice that of the Sun, and there is excellent evidence that the planet-metallicity correlation holds strongly for the M dwarfs that harbor relatively massive planets. Furthermore, it’s hard to argue with the two recent papers (one, two) from the California Planet Survey which report the detection of relatively massive planets orbiting two nearby M dwarfs, both of which have extremely high metallicities with the revised calibration.

The statistics are still small-number, but there’s a strong hint that the planet-metallicity correlation for Neptune and sub-Neptune mass planets orbiting M-dwarfs is stronger than it appears to be at FGK (where it’s effectively non-existent). Gliese 176, and Gliese 436, for example, are both quite metal-rich. I bet that a survey like Mearth could jack up its yield by shading its telescope visits to favor the high-metallicity stars on the observing list…

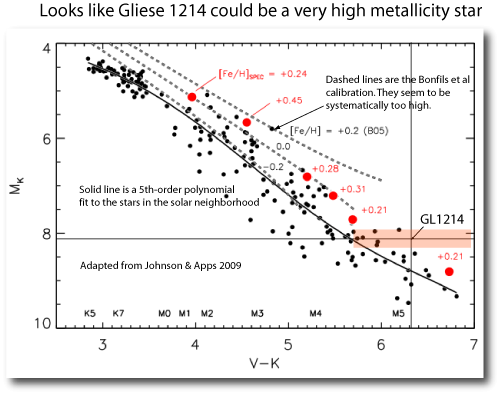
Indeed, if we plot Gliese 1214 (V=15.1±0.6, K=8.78±0.02, parallax=0.0772±0.0054”, distance modulus=0.562±0.16) in comparison to the stars in the local volume, it looks like Gliese 1214 has of order twice solar metallicity if we adopt the nominal values for V,K and the distance. That’s very intriguing…

lithium-induced speculations

Posted on by
3

Lithium Depletion

Israelian et al’s Nature paper on the planet-stellar lithium correlation (featured in last week’s post) caused quite a stir in the community. The depletion of lithium in the atmosphere of a solar-type star seems to be a prerequisite for the presence of a detectable planetary system. Here’s the paper’s plot again, this time, with Alpha Cen A added for effect. lithiumwalphacen

Had Israelian et al.’s paper come out a decade ago, much of the ensuing hubub would have focused on the fact that low lithium abundance is an effective signpost to planetary systems. Nowadays, though, mere detection of new planets is passé. Everyone knows there are tons of planets out there. Focus is shifting to finding the lowest-mass (and preferably transiting) planets around the brightest M, K, and G main sequence stars in the Sun’s neighborhood. There is a short, highly select, list of worlds that have been, and will eventually be, followed up to great advantage with HST, Warm Spitzer, and JWST.  All of the Sun’s most alluring stellar neighbors are under heavy and ongoing scrutiny, and in fact,  it’s these particular stars (in the form of the HARPS GTO list) that enabled discovery of the planet-lithium correlation.

So planet-finding utility aside, the intense interest in the planet-lithium effect stems from the fact that it’s guaranteed to be imparting an important clue to the planet-formation process.

With over 400 planets known, clear populations are starting to emerge. It’s remarkable that the strength of the lithium-planet correlation seems to be largely independent of the masses and periods of the planets themselves. The mass-period diagram for planets, on the other hand, shows that there are at least three distinct concentrations of planet formation outcomes:

currentpop2009

It’s important to keep in mind that Israelian et al.’s correlation holds over only a very narrow range of stellar temperature. The M-dwarfs (Gliese 581, Gliese 876), the K-dwarfs (HD 69830, Alpha Cen B), and the F-dwarfs (Upsilon Andromedae) all fall outside the band of utility. This dovetails nicely with standard models of stellar evolution that suggest the amount of Lithium depletion in stars with masses very close the the Sun (that is, stars falling in the narrow effective temperature range of the above plot) depends sensitively on both the efficiency of convection and also on rotational mixing. That is, the stars that show the lithium-planet effect, are exactly the stars where subtle differences in properties seem to generate a big effect on lithium abundance.

After writing last week’s post, I got an e-mail from Jonathan Irwin (of MEarth fame) who makes several interesting points:

The low lithium could be more of a coincidence resulting from the long-lived circumstellar disks that are presumably needed to form planets.

Mediation of the stellar rotation rates by long-lived disks is thought to be responsible for generating the wide dispersion in rotation rates observed in open clusters around 100Myr age, and there have been suggestions (e.g. Denissenkov et al.’s paper that appeared on astro-ph 2 weeks ago) that the slowly-rotating stars evolve developing some degree of decoupling of the rotation rates of their radiative core and convective envelope, whereas the rapidly-rotating stars evolve more like solid bodies.

Bouvier (2008) has suggested that the shear at the radiative convective boundary resulting from this could mix lithium into the interior more efficiently, and thus could result in lower lithium for stars that were slow rotators, preserving evidence of their rotational history even though the final rotation rates all converge by the solar age.  Some evidence for this last part exists in the form of a correlation between rotation and lithium in young open clusters such as the Pleiades.

A hypothesis along these lines seems quite appealing to me. As long as a protoplanetary disk is present, and as long as its inner regions are sufficiently ionized, then there’ll be a connection between the stellar magnetic field and the magnetic field of the disk. To a (zeroth) degree of approximation, the equations of ideal MHD allow us to envision the situation as consisting of a rapidly rotating star connected to a slower-rotating disk by lot of weak rubber bands. The net effect will be to slow down the stellar rotation to bring it into synch with the rotation at the inner edge of the disk.

Trying to sound like a tough-guy, I stressed the importance of predictions in last weeks post. If Irwin’s hypothesis is correct, then the formation of the Mayor et al. 2008 planet population is associated with disks that contain lots of gas, even in regions interior to R~0.1 AU. I’d thus expect that the “super Earths” are actually “sub Neptunes”, and that we can expect considerable H-He envelopes for the majority of these planets.

Another speculative prediction concerns the stars that aren’t depleted in lithium. In Irwin’s picture, these stars had short-lived disks and lost their gas relatively rapidly. This shouldn’t hinder the formation of terrestrial planets, but one would expect that the final configurations of the rocky planets would sport higher eccentricities, as there was little or no gas to damp the orbits down during the final stages of terrestrial planet accretion (see this paper for more on this).

Stockholm

Posted on by
Reply

Higher resolution version.

The opportunity to travel is a splendid benefit of being an astronomer. During this week and last, I’ve been to a whirlwind of European destinations.

Stockholm was the first port of call. For someone whose life is lived at 36.974 degrees North, it is surreal to arrive in the late evening to find the Sun still well above the horizon. Night never really falls. As the hours slip through midnight, the sky merely drifts through gradations of twilight. We don’t yet have addresses for terrestrial planets beyond our solar system, but it’s certain that the galaxy is full of them. We have as yet no clues to the alien geologies, landscapes, biospheres, but the spin axes of planets tend to be tilted. The quality of midsummer twilight in the high latitudes is a phenomena shared by worlds throughout the galaxy.

I gave two talks at the Alba Nova University Center, which hosts a collaboration between astronomers, physicists and biologists, and which is mostly located in a vast award-winning building by architect Henning Larsen. The astronomy offices are arrayed along a hallway that curves for nearly a hundred meters along the top floor. Running above the doorways is a continuous printout of the solar spectrum.

All told, it contains millions of resolution elements, and an absolutely bewildering forest of absorption lines.

Even on closest inspection, each angstrom of the spectrum is smooth and full of detail.

The juxtaposition of the micro and the macro readings is dramatic. The printout also drove home the utterly tiny scale of the Doppler shifts that must be measured in order to detect planets via the radial velocity technique. A large planet such as Tau Boo b generates a radial velocity half-amplitude of 500 m/s, which corresponds to moving (and slightly stretching or compressing) the entire hundred-meter-long diagram up or down the hallway by a few dots of printer resolution. The shift caused by Gliese 581 e, on the other hand, would require a microscope to detect.

Bode’s Law

Posted on by
6

Now I’m certainly not alone in thinking, upon seeing the latest configuration of the Gliese 581 system, Whoa, there’s room for a habitable Earth-mass planet in there…

Using the terrestrial planet valuation formula, an Earth-mass planet with a period of 25 days orbiting Gliese 581 is worth 136 million dollars, and needless to say, its detection would be an exciting development. Gliese 581 f seems like such a made-to-order confection that it’s simply got to be there.

Which is a flimsy argument, I admit, but quite frankly, when it comes to Gliese 581, I have no Alpha. I have no idea how and why the Gliese 581 planets wound up with their presently observed properties and configuration. Furthermore, even if one did have a handle on the sequence of events that led to the formation of b,c,d,e and f, and if one wrote that remarkable result up for publication, hardly anyone would believe it. And for good reason. It’s unlikely that the correct blow-by-blow account of what happened in the Gliese 581 protoplanetary disk would lead to any immediately verifiable predictions for any other planetary systems. We’ve observed enough planets now to know that the aggressive nonlinearity of the formation process leads to a bewildering variety of specific outcomes.

It occurred to me that it I might be able to make creatively disingenuous use of Bode’s Law to “predict” the presence of Gliese 581 f at the desired ~25d planetary period. As it stands, Johann Titius pointed out in 1766 that the orbital spacing of the solar system planets is well represented by d=0.4+0.3*(2^i), with i=-Inf, 0, 1, 2, 4, 5, etc. The law worked for Uranus (i=6) and Ceres (i=3), but then famously overperformed by placing a transuranian planet at 38.8 AU. Given that the Titius-Bode relation contains three parameters (a=0.4, b=0.3, and c=2) it’s possible to choose a,b, and c to exactly reproduce Gliese 581 e, b, and c. Unfortunately, the results for d and and f are then rather less than satisfactory, so I decided to abandon a Bode’s law scheme in favor of a straightforwardly bald assertion of Gliese 581 f’s existence.

It’s perhaps for good reason that the Icarus Editorial Office states:

Icarus does not publish papers that provide “improved” versions of Bode’s law, or other numerical relations, unless they are accompanied by some detailed physical/chemical arguments to explain why the new relation is to be preferred.

In the next post, I’ll look in detail at how and when Gliese 581 f can be detected: scenario four.

Aliased

Posted on by
4

Woke up this morning to the startling news that the Geneva team has added an Msin(i)=1.9 Earth mass planet to the Gliese 581 system! The preprint (Mayor et al. 2009) is available from exoplanet.eu, and will appear in Astronomy and Astrophysics. With a radial velocity half-amplitude, K=1.85 m/s, Gl 581e is the lowest-mass planet detected to date.

“The orbital period of the new planet “e” is quite close to pi days. i would mark down a score of -1 for competing planet hunters, whose signals-to-noise are accumulating in proportion to the root of the number of measurements.” said Greg Laughlin, an astronomer at the University of California, Santa Cruz.

In addition to the detection of the new 1.9 Earth-mass planet in the system, the period of Gliese 581d has been revised (to great habitability fanfare) from 84 days to 66 days. Indeed, the new, shorter period raises the habitability value of Gliese 581d from about 0.5 cents to nearly one penny.

As often happens, a strong hint of the new planet was lurking unnoticed in the previously published radial velocity data, and it’s especially interesting to look at the details in this particular case to see how the period revision came about. Let’s work with the 50 radial velocities published by Udry et al. 2007.

The two strongest periodicities in the system come from planets b and c. Removing these planets with the assumption of circular orbits leaves a residuals periodogram that has its strongest peak at 84 days:

The 66 day periodicity is lagging in second place with 66% of the power. Nevertheless, both periodicities provide significant improvement to the fit. An 84-day planet has K=2.67 m/s, and leaves an RMS of 1.43 m/s to the three planet fit:

A best fit 66-day planet has a slightly higher K=2.77 m/s, but leaves an RMS of 1.72 m/s. The chi-square is also higher: 5.10 as compared to 3.65. In the 2007 data, the 84-d planet thus looked quite secure. With hindsight, though, one notices that the phase coverage in the 66-day fit is better than for the 84-day fit. As more data was obtained, it became clear that the 84-day period was an alias of the true 66-day periodicity. Fair enough — RVs are expensive to obtain, and revisions of this sort are an inevitable product of progress.

In the residuals to the fit with the 84-day planet, planet e is present, but it’s masked by a spurious periodicity at 3.45 days,

whereas in the residuals to the fit with the 66-day planet, planet-e is in the #1 spot — not yet significant, but certainly more tantalizing…