Credit: NASA/JPL

It feels increasingly awkward and embarrassing to read LaTeXed, peer-reviewed articles that quantify and delineate the habitable zone — the special region surrounding a star that is invariably (and rather fittingly) linked to a particular fairy tale from the Brothers Grimm.

Evolutionary psychologists have speculated that the concept of the afterlife might be inextricably entwined to the evolution of the mind’s ability to reason about the minds of others. A rational world view, however, frustrates ingrained atavistic yearnings and a belief in the supernatural. Habitable planets provide a respectable stopgap to assuage the discomfort of these incompatible poles. Could it be a mere coincidence that the ancient Greek and classical depictions of Elýsion pedíon, the Elysian Fields, are part and parcel the very image of the habitable zone?

Credit: NASA/SETI/JPL

And they live untouched by sorrow in the islands of the blessed along the shore of deep-swirling Ocean, happy heroes for whom the grain-giving earth bears honey-sweet fruit flourishing thrice a year, far from the deathless gods…

— Hesiod, Works and Days (170)

The submerged summit of the Detroit Seamount ranks among the planet’s gloomiest spots. East of Kamchatka, a mile beneath the waves at 51 51′ N, 167 45′ E, it is second-to-last in the long line of Emperors. Inch by inch, it creeps toward destruction in the Aleutian Trench.

Detroit’s glory days were the late Cretaceous. Back then, it was an active Hawaiian volcano.

Live it fast, you’re gonna get there soon. Kauai is five million years old, but underground, the lights have gone out. Over half of the original height and the original land area have disappeared. Rivers gush sediment into the sea. Waimea Canyon juxtaposes verdure and an erosive wasteland. Four wheel drive claws and rends the red dirt.

Beyond Kauai, the next islands in the chain are Nihoa,

Necker,

and the La Perouse Pinnacle,

whose resemblance to a sinking ship is not just metaphoric.

Before humans arrived, the Hawaiian islands had strange flightless birds. Indeed, each island in the chain developed its own odd avian inhabitants, sculpted by natural selection, and then driven conveyor-like to extinction. Not once, in forty, fifty, sixty tries, did the birds respond by evolving intelligence and doing something about their situation. Probably, there was never enough time.

Or perhaps, that’s something that rarely, if ever, happens.

It’s worth a scramble to get a window seat on a Hawaiian inter-island flight. The views are full of craggy green cliffs, porcelain ocean, and wispy masses of fog and cloud. Sometimes, several islands are visible at once, and it’s not hard to imagine that the archipelago might extend over the entire globe.

That would be a very different planet, and, in fact, a world covered by hotspot volcanoes might have a surface elevation profile somewhat reminiscent of the WMAP image of the temperature fluctuations in the cosmic microwave background. The WMAP image brings to mind a planet covered in Hawaiian islands.

Any distribution, \(f(\theta,\phi)\), on the surface of a sphere, be it of temperature, or elevation, or the density of IP addresses, can be expressed as a weighted sum of spherical harmonics

$$f(\theta,\phi)=\sum_{l,m} a_{l,m} Y(\theta,\phi)_{l}^{m}\, ,$$
where the coefficients corresponding to the individual weights, \(a_{l,m}\) are given by
$$a_{l,m}=\int_{\Omega}f(\theta,\phi)Y(\theta,\phi)_{l}^{m \star}d\Omega\, ,$$
and the power, \(C_{l}\) at angular scale \(l\) is
$$C_{l}=\frac{1}{2l+1}\sum_{m=-l}^{l}a_{l,m} {a_{l,m}}^{\star}\, .$$

The power spectrum of the CMB anisotropies peaks at \(l\sim 200\), which corresponds to an angular scale on the sky of \(\Delta \theta \sim 1^{\circ}\), which is very close to the solid angle subtended by the Big Island of Hawaii on the surface of the spherical Earth.

Here’s a recent version of the CMB temperature anisotropy spectrum from the Planck Mission website

The peaks in the spectrum of CMB temperature anisotropies stem from acoustic oscillations and diffusion damping in the early universe, and they encode all sorts of information about the fundamental cosmological parameters. This, of course, is very well-known stuff: a search on all literature in the ADS database published since 2000, and ranked by citations, lists Spergel et al. 2003, First-Year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Determination of Cosmological Parameters at #1, with 7,914 citations and (rapidly) counting.

Given the similarity between the angular scales of the Hawaiian islands and the main CMB peak, it’s interesting to compute the angular power spectrum of Earth’s bedrock elevation profile. A global relief dataset with one arc-minute resolution is available from NOAA as a 4GB (uncompressed) file. Downsampling by a factor of 100, and applying the “terrain” color map yields a familiar scene

Computing the power in the first 108 angular modes of the relief distribution in the above data set gives a spectrum that is weighted toward continents and ocean basins rather than archipelagos. There is a pronounced peak at \(l=5\) that reflects the typical angular scale of continents and ocean basins.

Here is the global relief distribution obtained by summing just the \(l=5\) contributions. It’s right for more or less the same reason that Crates of Mallus was right:

Using all 108 angular mode families to reconstruct the image gives a fairly credible-looking world map. It’s as if the watercolors ran slightly before they dried. Most critically, the \(l=108\) reconstruction fails to capture the highest peaks and the lowest ocean trenches, and hence more of the dynamic range of the color map is distributed across the globe.

Degree-wide islands like Hawaii are the exception rather than the rule on Earth’s surface. I believe that this was the concept that former US Vice President Dan Qualye was struggling to express in one of his much-ridiculed pronouncements:

Hawaii has always been a very pivotal role in the Pacific. It is IN the Pacific. It is a part of the United States that is an island that is right here.

(See also his comments on Mars.)

A few weeks ago, I had a flight out of LaGuardia Airport in New York City. On the drive there, I caught a distant glimpse of the Manhattan skyline. I was startled to see that it is newly altered. Rising from midtown was a silhouette that seemed both impossibly narrow, and taller than any other skyscraper in the far-off cut-out.

Original Photo: 432parkavenue.com — Photoshop processed screenshot

The Internet, of course, has the story. 432 Park Avenue — $1.25B, 426 meters, the highest rooftop in the city. Many of its floors, especially the higher ones, are monolithic residences, in the process of acquisition by opaque, limited liability corporations, “bank safe deposit boxes in the sky that buyers can put their valuables in and rarely visit.”

Often, the aesthetic informing such projects veers toward the rococo, but 432 Park is minimalist to the core. Every window of the tower is an exact 10 foot by 10 foot square. From the elaborate on-line galleries, it wholly ambiguous whether the surreal bone-parchment interiors already exist or whether they are virtual. Somewhere, in micrometric accuracies of the digital architectural model, lies the pattern of the seasons, the moment of the equinox, the precise angle of sunlight shafting into the cavernous, unvisited, perhaps as-yet unconstructed rooms.

Like the pyramids at Giza — after they were sealed and before they were robbed.

This Fall quarter, I taught a class for undergraduates on order-of-magnitude estimation in physics with a focus on astronomical examples. And on the last day of class, with final exams looming, what could be better that the time-tested stress relievers provided by the Fermi Paradox and the Drake Equation?

In Los Alamos National Laboratory publication LA-103110MS, “Where is Everybody?” An Account of Fermi’s Question, Eric Jones describes how Enrico Fermi, Emil Konopinski, Edward Teller, and Herbert York were diverted into their famous lunch-time conversation in the summer of 1950. While walking to the cafeteria, they were discussing news reports of UFOs, and an associated New Yorker cartoon that explained why the public trash cans in New York City were disappearing.

The flying saucers of the early 1950s hold a special fascination. A compound of Cold War anxieties — nuclear weapons, communists, infiltrators — they are silvery and remote, icons of minimalist design from a time when the space age was truly, rather than retro- futuristic.

Indeed, much of my own interest in astronomy can be traced to 50’s-era flying saucers. In the Bicentennial summer of 1976, after finishing third grade, I got a paper route delivering the Champaign-Urbana Courier. One of my customers, Mrs. Barbara Houseworth, had a garage full of cast-off books that she collected for an annual drive. I spent a great deal of time examining them whenever I visited to collect the subscription fee. I was particularly drawn to the pulpy paperback books — especially the ones with clay-coated photographic inserts — that covered the Bermuda Triangle, Bigfoot, the Loch Ness Monster, and Flying Saucers. All matters that seemed to merit the most urgent scientific concern.

At the top of my list was Gray Barker’s They Knew Too Much About Flying Saucers, published in 1956. I was so taken with it that Mrs. Houseworth simply gave me the book.

Gray Barker was an intriguing character, a closeted gay man in mid-century West Virginia who took a certain delight in channeling the fears and neuroses of the American masses into money-making volumes. Barker’s invention of the three men in dark suits, in particular, achieved a lasting cultural resonance. There is more about him at the UWV Center for Literary Computing, and he is the subject of several recent documentaries.

The message in the Cold War flying saucer books was crystal clear. Watch the Skies. And I did — on many clear dark Central Illinois nights with a Sears catalog 50mm refracting telescope…

Back to Friday’s class. We adopted the following form for the Fermi-Drake equation
$${N} = \Lambda ~f_{\star \rm{app}}~f_{\rm pl}~f_{\rm quqHP}~f_{\rm life}~f_{\rm macro}~f_{\rm intel}~f_{\rm tech}~L\,,$$
where \(N\) is the number of broadcasting civilizations in the galaxy, \(\Lambda\) is the number of stars formed per year in the Milky Way, \(f_{\star \rm{app}}\) is the fraction of stars with main sequence lifetimes long enough to support the development of a broadcasting civilization, \(~f_{\rm pl}\) is the fraction of stars with planets, \(~f_{\rm HP}\) is the average number of “habitable” planets per star, \(~f_{\rm life}\) is the fraction of these habitable planets that develop life, \(~f_{\rm macro}\) is the fraction of life-bearing planets that develop macroscopic life, \(~f_{\rm intel}\) is the fraction of macroscopic life-bearing planets that develop an “intelligent” life form (e.g. one that can orient itself abstractly in time), \(~f_{\rm tech}\) is the fraction of intelligent species that develop an understanding of the Maxwell Equations and build radios, and \(L\) is the civilization lifetime in years.

We defined and estimated two versions of \(L\). \(L_{\rm radio}\) is the average length of a time that a civilization leaks modulated electromagnetic signals into space. \(L_{\rm extinct}\) is the lifetime of the civilization, marked from the understanding of Maxwell’s equations to the point where the equations are collectively no longer understood.

The first few terms in the equation have been elevated from the realm of science fiction. I’ve adopted values of \(~\Lambda=10\,{\rm stars~yr^{-1}}\), \(~f_{\star \rm{app}}=0.75\), and \(~f_{\rm pl}=0.75\). Note that \(~\Lambda=10\,{\rm stars~yr^{-1}}\) is admittedly on the high side, even for 4.5 Gyr ago when star formation was somewhat more prevelant in the Galaxy.

Here is the table of values for the unknown terms, as estimated by the class members. I tried not to influence the results by telegraphing currently fashionable guesses. Twenty responses were collected:

With results:

Civilizations Currently Broadcasting in the Milky Way Galaxy
Average # 16,875
Median # 0.0016
Standard deviation 73,500
Max 337,500
Min 2.8125e-13

Civilizations Currently Present in the Milky Way Galaxy
Average # 185
Median # 0.013
Standard deviation 735
Max 3,375
Min 2.8125e-13

A smooth distribution of estimates for \(~{N}\) can be generated by drawing randomly from the list of estimates for each uncertain term in the equation, and then repeating for many estimates of \(~{N}\). Here are the histograms of estimates for the number of civilizations broadcasting from the galaxy and the number of civilizations present in the galaxy. The \(x\)-axes are \(\log_{10}N\).

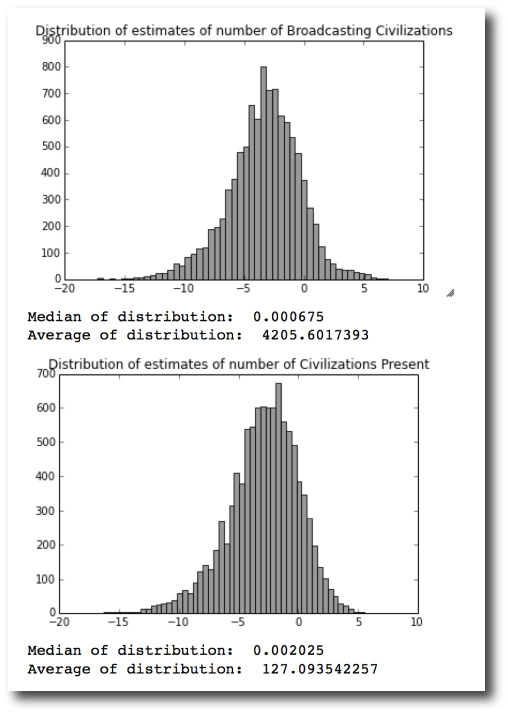
The estimates point to the possibility that a civilization broadcasts for longer than intelligent members of the species exist. Two people implied this, by submitting values \(L_{\rm radio}>L_{\rm extinct}\). Looking at the table, there is one case where \(L_{\rm radio}\gg L_{\rm extinct} \gg \langle L \rangle\). The large values for \(L\) submitted by this person are causing the Average estimate for \(~{N}\) to substantially exceed the median estimate for \(~{N}\).

Adopting the \({ N=0.002}\) median of this distribution implies we need to look through \(\sim{n=500}\) galaxies to find the nearest broadcasting civilization, and that our nearest neighbors are \(\sim{ 8}\) Megaparsecs away. By the time one receives a message and replies to it, the intended recipient has long since gone extinct.

In 1997, Ray Bradbury’s The Martian Chronicles was reissued by William Morrow Press. It’s a book that’s on my shelf.

In the original edition, published in 1950, the stories were set in what is now the present day, starting with Rocket Summer, dated to January 1999, and ending with The Million Year Picnic, set in October 2026.

For the 1997 edition, the dates for the stories were all pushed back by thirty one years. The rocket summer still lies sixteen years in the future, but the imposed literary device seems hollow, stop-gap, ineffective. Mars of 1950 is a forever different world than Mars of today, which, satisfyingly, is also populated by two waves of explorers from Earth. Meteor-borne archeobacteria, perhaps still clinging to existence in the warmth of the deep subsurface, and a cadre of faintly autonomous, sometimes faintly anthropomorphic robots and satellites that pine eagerly for attention on social media. 2836 tweets. 1.76M followers.

The layout of the solar system is at least moderately atypical. There should be roughly four Earth masses worth of planets inside Mercury’s orbit. And Jupiter, with its large mass, its close-to-circular orbit, and its 10+ year period is an oddball at the 10% (and probably more impressive) level.

At the start of the 1990s, the narrative for how the future, futuristic discovery of extrasolar planets would unfold was informed by the contents of the solar system. I was supposed to be doing my thesis work on modeling the infrared spectra of protostars. But somehow, L1551, and its spartan low-res spectrum, seemed dull and unappealing and far away from any every-day concern. Then, as now, the evolution of protostellar disks sternly needed to be understood. Look at the first page of any review article on protostellar disks from two decades ago. Save the references, it could be employed in almost unaltered form today. I avoided walking past my adviser’s door due to my creeping, near-complete lack of any progress.

At that time, Doppler velocity measurements and astrometry were scheduled to gradually improve to the point where the orbital influences of Jupiter’s extrasolar analogs would eventually become apparent, and that time lay hazily in the future. Brown dwarfs (of which no airtight examples were known) were a way station for the impatient. There seemed something electrifying about the possibility that a dim failed star might be drifting by, just few light years away. I decided to drop the the disk spectra. All at once, I felt energized and engaged. Soon, we had a paper submitted. It was neither a memorable nor an important contribution, but it was the product of a genuine curiosity and focused effort. The upshot of lots of modeling and evolutionary calculations and hand-wringing and earnest e-mails was that “our work affirms the likelihood that the stellar mass function in the solar neighborhood is increasing at masses near the bottom of the main sequence and perhaps at lower masses”. More to the point, the best, wholly uncontroversial guess was that there would end up being about 10 brown dwarfs within 5 parsecs.

In late 1995, 51 Peg b somehow short-circuited the brown dwarfs’ front-row mystique. As the extrasolar planet count mounted, I paid little (or sometimes no) attention to the steady accumulation of discoveries within the Sun’s immediate 5-parsec environs.

Last week, while preparing for my class on order-of-magnitude estimation, I looked at Wikipedia’s list of nearest stars and brown dwarfs. I was surprised to realize that there are now thirteen brown dwarfs and counting within five parsecs, several more than we had guessed back in 1992. I was particularly startled by WISE 0855-0714, which was discovered just this year by Kevin Luhman. It is precisely the object whose prospect seemed so exciting half a lifetime ago. One percent the mass of the Sun. Photosphere plunged into icy deep freeze. Utterly black to the eye, save the occasional faint crackling glow of lightning from deep within.