As Mick Jagger famously remarked, you can’t always get what you want. Kepler’s photometric transit observations provide excellent measurements of the planetary orbital periods, the transit epochs and the planet-to-star radius ratios, but they are stingy and tight-lipped when it comes to the planet’s masses, eccentricities, and longitudes of periastron.

Occasionally masses can be inferred from transit timing variations, especially if a system contains more than one transiting planet. Alternately, one can assume a planetary mass-radius relation (keeping in mind, of course, what happens when u assume). For example, M=R^2.06 in units of Earth masses and radii works quite well in our solar system for V-E-S-U-N. Or, dispensing with the trickery, one can pony up and measure radial velocities.

With photometric data alone, information about the orbital eccentricity distribution of the planet census can be deduced by statistically comparing transit durations to orbital periods. The idea is a full elaboration of the simple observation that if a central transit that is substantially shorter than expected, then it’s quite possible that the planet is occulting the parent star near the periastron of an eccentric orbit.

In one of the flurry of Kepler-related papers that accompanied the February data release, Moorhead et al. (2011) implemented just such a program, and generated a statistical analysis of the distribution of transit durations for the Kepler exoplanet candidates. They assumed that the eccentricities conform to a Rayleigh probability distribution function:

where the controlling parameter, sigma, is is related to the mean orbital eccentricity through

To get a sense of what the Rayleigh distributions look like, here are examples for e_av=0.05, e_av=0.21, and e_av=0.50, compared to the distribution of eccentricities in the exoplanet.eu catalog:

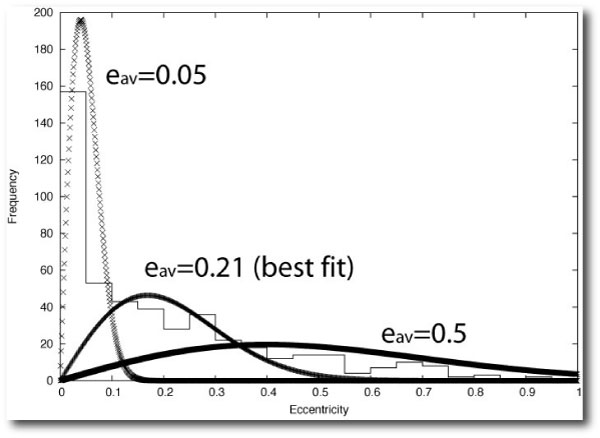
Ignoring planets that are likely tidally circularized, the best fit occurs for e_av=0.21. This model, however, underproduces planets at high eccentricity — ‘606 wouldn’t have turned up if e_av=0.21 were a hard truth. Moorhead et al.’s analysis of the Kepler data comes up with plausible best-fit values for e_av ranging from 0.1 through 0.25, for cooler stars with effective temperatures less than 5100K. So there is rough agreement, even though the two catalogs have radically different sampling biases.

A significantly non-zero value for average orbital eccentricity has some interesting consequences for transit surveys. At a given semi-major axis, eccentric planets have (on average) a higher chance of transiting. This is easily seen by comparing an e=0.5 orbit with a circular orbit having the same semi-major axis.

For a population of planets having a specific Rayleigh distribution of eccentricities, the average transit probability at a given semi-major axis is increased by a factor

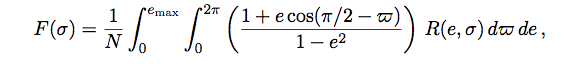
where the normalization factor, N, is given by

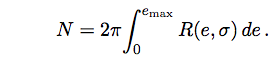
For e_av=0.25, this boosts the total population of planets by about 10% over what one would infer from the standard 1/a circular orbit scaling.

I’ve been reading a textbook on ore-forming processes as part of an attempt to get a little more fluent in geology, and I ran across a plot that is certainly well known to many, but was an eye-opener for me:

The plot charts the solubility by weight of water in several common igneous rocks as one moves deeper into the lithosphere. The take-away message is that even at modest depths, rocks can be very heavily hydrated and are capable of harboring a very large amount of water.

The plot brought to mind something that, to my highly inexpert eye, has always seemed a remarkable coincidence. The volume of water in Earth’s oceans has an average depth of ~4000 meters, leading to a sea-level that does a pretty fair job of outlining the continental margins (which mark the boundaries between denser (but thinner) basaltic crust and lighter (but thicker) granitic crust. Only about 20% of the total continental crust is overlaid by water.

In the extrasolar planet context, an interesting question is whether the situation here on Earth is unusual. Many of the planets that Kepler has found (and will be finding) contain water mass fractions that are considerably larger than Earth’s. Is it reasonable to expect that they’ll have deep oceans that uniformly cover the planets, or is there some sort of mechanism involving water of hydration that maintains a seafloor-continent dichotomy even in the presence of a lot of water? As far as I can tell, this question hasn’t been answered definitively.

The naive answer seems to be along the following lines. Imagine that a terrestrial planet forms in such a manner that the mantle rock is heavily hydrated. Given that mantle rock can easily retain a water mass fraction measured in tens of percents, one could start out with a planet that contains many oceans worth of water, but in which substantial portions of the surface are dry.

When rock melts, the water of hydration is squeezed out. (Migration of this water into the surrounding country rock leads to the mineralized veins that are the basis for many of Earth’s great ore deposits.) On an ongoing volume-weighted basis, most of the melting is taking place beneath the spreading centers that form the mid-oceanic ridges. Every year, of order 300 cubic kilometers of melt are produced, several cubic kilometers of which are erupted to form fresh ocean crust. Coupled with mantle convection, this means that the mantle unburdens its water on a timescale of order a billion years. Some of the water is subducted back down, but this sink is less effective than the source, meaning that the water likely ends up on or near the surface.

So one can imagine planets (perhaps with mantle convection less vigorous than Earth’s) in which continents are gradually submerged as water is squeezed out of the mantle. Not, perhaps, a bad way to go. The world’s best beaches are those of the Seychelles islands — a handful of granitic specks in the vastness of the Indian ocean — the highest peaks of the submerged continental Mascarene Plateau.

Klaus Nomi and David Bowie (Image source and backstory)

I was in the middle of my dynamics lecture this past Monday morning, explaining the Fokker-Planck approximation to the collision term on the right-hand-side of the Boltzmann equation, when my phone started buzzing and vibrating in my pocket. Good thing I had remembered to turn the volume off. Without having to look at who might be calling, I knew it was likely some media outlet, BBC? KCBS? There was a sudden, all-to-familiar sensation of queasy uneasiness which made it very hard to focus on the second-order terms I had just written on the whiteboard.

Back in 2001, I naively and foolishly spoke to a reporter at the London Observer about the “relative ease” of accomplishing strictly hypothetical orbital engineering in the context of a billion-year time frame. The resulting article (now archived by the Guardian) contained an alarmingly incorrect cognitive leap from the ultra-long term to the immediate near-term:

The misconception came exactly at the time when George W. Bush was visiting Europe, explaining his position regarding the Kyoto Protocol. The Observer story became a huge, completely nightmarish story in Europe, which then echoed across the Atlantic, where it was seized upon by the Drudge Report, Rush Limbaugh and others. Here’s an example editorial from the Manchester New Hampshire Union-Leader:

For nearly a week, the story managed to survive, zombie-like through successive news cycles. Eventually, Gary Condit appeared on the scene, and finally, the media’s full attention was diverted elsewhere.

As readers likely know, I’ve been writing on this web log about a planet valuation formula, which is designed to give a quantitative assessment of whether a newly discovered planet is worthy of significant media attention. Last month, I had a detailed conversation with Lee Billings, which was published on BoingBoing as a part of Lee’s series of posts on planets (which are well worth reading!)

Several weeks after the BoingBoing article appeared, I got a very politely worded e-mail from a reporter at News of the World.

[…] I found your article on the value of the Earth which popped up on a UK blog late last week.

From what I can ascertain, your findings and formula haven’t really had the coverage they deserve in the UK media and I was hoping to rectify that…

After a look at the Wikipedia page on News of the World, my heart was pounding. “Wacko US Prof Sez: Sell Earth for 3 Quadrillion Quid!” I sat down at the computer, and it took a long time to compose a reply.

Turned out that the reporter was admirably interested in getting the story right, and the final version (which is behind a paywall) is quite fair. After all, given the possibly arch, arguably pretentious tone here on oklo.org, I did pretty much have it coming.

Predictably, newspapers in Britain saw the News of the World story and immediately picked it up. As is to be expected, successive iterations tend to lose focus on the exoplanets, and gain focus on the value of Earth. Radio stations are calling, trying to set up interviews about how much Earth is worth. Angry e-mails drift into my inbox. Google news is at 61 articles and counting.

I think it’s time to look into installing Google’s AdSense…