It’s no exaggeration to assert that Galileo’s unveiling of Io, Europa, Ganymede and Callisto counts among the epic scientific discoveries of all time.

And certainly, it’s fair to say that the Galilean satellites of Jupiter constitute the original exoplanetary system. The Galilean satellites have been producing scientific insights for over four hundred years. Nearly all of the modern exoplanetary discoveries have antecedents — some quite recent, some centuries old — in Jupiter’s four moons.

The Galilean satellites can all be observed in transit across the face of Jupiter, and as early as 1656, the Sicilian astronomer Giovanni Hodierna, with his Medicaeorum Ephemerides, emphasized the importance of transit timing measurements for working out accurate predictive tables. In the late 1660’s, University of Bologna Professor Giovanni Cassini’s timing measurements and associated tables for the Jovian system were so impressive that he was tapped by Jean-Baptiste Colbert and Louis XIV to become director of the newly established Paris Observatory.

Giovanni Domenico Cassini (1625-1712). Prior to holding the directorship of the Paris Observatory, he was the highest paid astronomer at the University of Bologna, having been appointed to his professorship by the Pope.

Throughout the 1670s and 80s, Cassini wrestled with the fact that accurate transit timing measurements for the Jovian satellites create serious difficulties for models in which the moons travel on fixed orbits. Irregularities in the transit timings made from the Paris Observatory led to Ole Roemer’s determination of the finite speed of light in 1676, and by the early 1700s, observations of transit duration variations revealed that rapid nodal precession occurs in the Jovian system.

By middle of the Eighteenth Century, adequate data were in hand to demonstrate that a very curious relationship exists between the orbits of Io, Europa, and Ganymede. In 1743, the Swedish astronomer Pehr Wilhelm Wargentin (the first director of the Stockholm Observatory) published tables which made it clear that the 1:2:4 ratio in periods between Ganymede, Europa and Io is uncannily exact. Wargentin’s tables implied that a triple eclipse (in which all three satellites transit at once) would not occur until 1,319,643 CE at the earliest, and that the “argument”

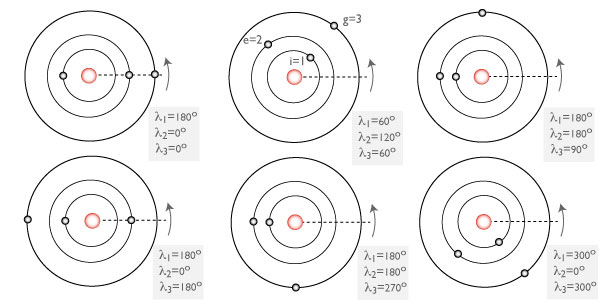
between the mean longitudes of the satellite orbits is maintained to an extraordinary degree of accuracy. Geometrically, this means that the satellites engage in a cycle of six successive moon-moon conjunctions during the course of one Ganymedian orbit, and in so doing, manage to continually maintain ?_L=180°:

Laplace realized that a dynamical mechanism must be responsible for maintaining the cycle of conjunctions, and in 1784, was able to show that the angle ? is subject to a pendulum-like oscillation. If the satellites are perturbed slightly, then over the time, the satellite-satellite interactions conspire to cause ? to oscillate, or librate, back and forth about the equilibrium value of 180°. His theory for the satellites allowed him to derive the masses of the moons, and also predicted that the oscillation period for ? would be 2270d 18h.

In Laplace’s time, the observations were not accurate enough to sense any measurable amplitude for the libration — it appeared that the satellites were perfectly placed in the 1:2:4 resonant condition. We now know, however that ? librates with a tiny amplitude of 0.064°, and that the period of oscillation is 2071d, quite close to the value predicted by Laplace. Yoder and Peale (1981) have shown that the highly damped libration of ? can be understood as arising from a near-balance between tidal dissipation in Jupiter and tidal dissipation in Io. The presence of a dissipative mechanism has allowed the marble to have settled almost precisely into the bottom of the bowl.

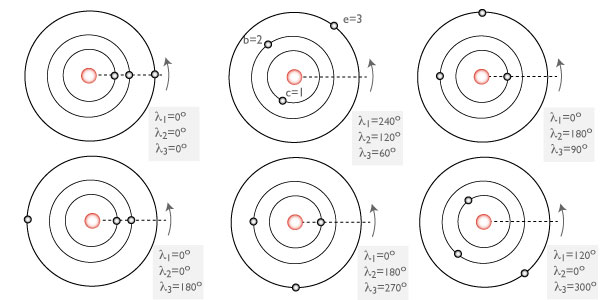
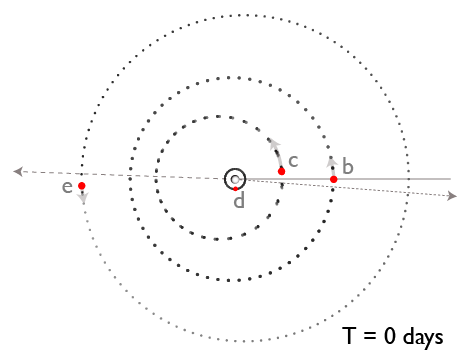
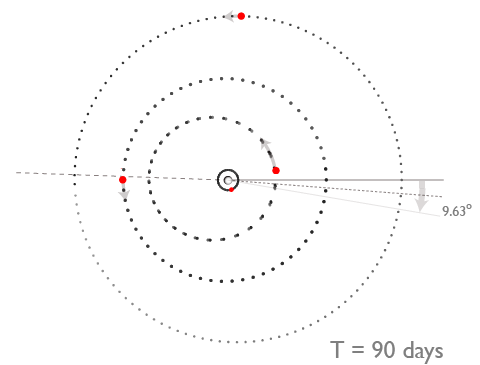
On this evening’s astro-ph mailing, our team has posted a paper that describes our discovery of a second example of a Laplace three-body resonance. Continued radial velocity monitoring of the nearby red dwarf star Gliese 876 has shown that the well-known P~30d and P~61d giant planets in the system are accompanied by an additional planet with a mass close to that of Uranus and an orbital period P~124d. In contrast to the Jovian system, the best fit to the observations shows that the Laplace relation is librating around ?=0°, and that triple conjunctions do occur. The diagram above is easily modified to convey the schematic geometry of the new system:

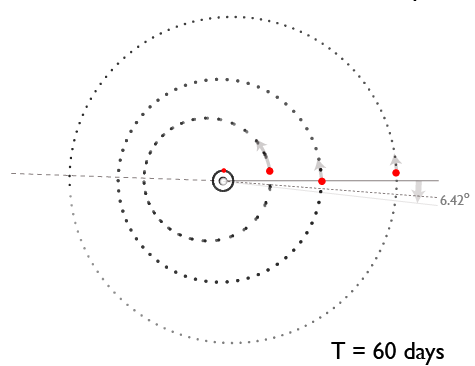
The actual state of affairs, however, is more complicated than shown in the above diagram. The total mass of planets in the Gliese 876 system is about 1% the mass of the central body, whereas Jupiter is roughly 5000 times more massive than its satellite system. This means that the Gliese 876 planets experience proportionally larger mutual gravitational interactions than do the Galilean satellites. In addition, the orbits are much more eccentric, and the planet-planet secular interaction causes a rapid precession of 14° per orbit of the outer planet. We can, however, plot the orbits in a co-precessing frame in order to view the cycle at four equal time intervals:

The libration of the Laplace argument, ?, around zero has an amplitude of ~40°, indicating that the GJ 876 “pendulum” packs a swing that’s 625 times larger than that of the Galilean satellites. Indeed, when the system configuration is integrated forward in time for hundreds of years, it’s clear that a simple pendulum equation is not able to describe the evolution of the Laplace angle. The oscillations are chaotic, with a Lyapunov time measured in a mere hundreds to thousands of years, and the theory, especially if there is a non-coplanar component to the motion, will require Laplace-level expertise in the use of the disturbing function…

There’s more… stay tuned for the next post.

Some of the biggest exoplanet news so far this year has arrived in the form of Rossiter-McLaughlin measurements of the sky-projected misalignment angles, λ, between the orbital angular momentum vectors of transiting planets and their stellar spin vectors.

A significantly non-zero value for λ indicates that a system was subject to some rough action in the distant past. Both planet-planet scattering and Kozai migration, for example, can lead to systems with non-negligible λ’s. The recent paper by Triaud et al. (covered here) showed that such processes may be responsible for a startlingly significant fraction of the known transiting-planet systems.

The angle λ has the advantage of being measurable, but it has marked disadvantage of informing us only of the projected geometry of the system. To get a sense of the physically relevant quantity — the true degree of spin-orbit misalignment — one needs the direction of the stellar spin vector.

Kevin Schlaufman, one of the graduate students in our program here at UCSC, has worked out a very clever method of getting a proper statistically supportable guess of the complement misalignment angle between the orbit of the plant and the spin of its host star along the line of sight. I have to say that I’m quite enthusiastic about Kevin’s paper — it’s a big jump, not an incremental advance, and it’s well worth reading.

The method leverages the fact that a mature main-sequence star of given mass and age has a fairly predictable rotation period. Sun-like stars form with a wide range of rotation periods, but by the time they reach an age of ~0.5 billion years, there is a reasonably well-defined rotational period-stellar mass relation. During the remainder of their lives, main sequence stars then slow their rotation by shedding angular momentum via Alfven-like disturbances. Stellar spin-down rates are relatively large early on, and decrease with the passage of time.

A star’s projected rotational velocity can be measured by looking at the amount of rotational broadening in the spectral lines. This gives V_rot*sin(i_s), where i_s is the unknown angle between the star’s spin pole and the line of sight. The essence of the Schlaufman method is then immediately apparent. The mass and the age of the star allow you to infer V_rot. You measure V_rot*sin(i_s), and then bam! The inclination angle, i_s, is determined.

Reality, of course, is not so clear-cut. One has a host of errors and intrinsic variation to deal with, all of which blur out one’s ability to precisely determine i_s. Nevertheless, Kevin shows quite convincingly that the method has utility, and that it is possible to identify transit-bearing stars that are very likely strongly misaligned with the plane of the sky.

The results of the analysis confirm that massive and eccentric transiting planets (such as oklo.org fave HD 17156b) are substantially more likely to have significant spin-orbit misalignment than are garden variety Jupiter-mass hot Jupiters on circular orbits. Furthermore, to high confidence, it seems that systems with substantial spin-orbit misalignment tend to have host stars with masses greater than 1.2 solar masses. A reasonable conclusion is that there are two distinct and productive channels for generating short-period giant planets. The first is a disk migration process that leaves everything calm, orderly and aligned. The second, most likely involving Kozai cycling or a variant thereof, is telegenic, action packed, and leaves a system confused and misaligned, and perhaps stripped of several original fellow planets.

It’s not often that a near-doubling of the planetary census arrives in one chunk, and so the paper detailing the latest Kepler results is of quite extraordinary interest.

It’s definitely going to be tricky to use the results in the Kepler paper to draw secure new conclusions about the true underlying distribution of planets. Nevertheless, the results look quite intriguing from the standpoint of back-of-the-envelope speculations.

Details: the paper contains a list of 312 candidate planets originating from 306 separate stars. A further 400 stars with candidate planets have been held back (see yesterday’s post), largely because they are either bright enough for high-quality Doppler follow-up at less-than-exorbitant cost, or harbor candidates with radii less than 1.5 that of Earth, or both. The paper states that the 312 candidate planets were primarily culled from an aggregate of 88,196 target stars dimmer than magnitude 14. The analysis is based on two blocks of photometry, one lasting 9.7 days (starting on May 2 2009) and one lasting 33.5 days (starting on May 13 2009).

The candidates have a slightly eclectic selection of associated data. The main table lists a radius, a transit epoch, and an orbital period for each candidate. There’s information about the parent stars as well, including apparent magnitude, effective temperate, surface gravity, and stellar radius. This is enough to make some intriguing plots. For example, the splash image for this post is a Hertzsprung-Russell diagram charting the locations of the candidates’ parent stars. The sizes of the points are directly proportional to the planet radii, and the color code is keyed to estimated planetary effective temperature. Most of the planets have surface temperatures of order 1000K or more, but there’s one rather singular object in the list, a 1.34 Rjup candidate on a 10389.109(!)-day orbit about a 9.058 solar radius G-type giant that (if it’s a planet) would have a photospheric temperature of order 180K. Certainly, a 1.34 Rjup radius is intriguing for such an object, as any non-pathological cold giant planet should be the size of Jupiter or smaller. Presumably, if the light curve showed evidence of a Saturn-style ring system, or better yet, an Earth-sized satellite, then KIC11465813 would chillin’ in the V.I.P. room.

A question of great interest is whether the list of candidates can add support to the recent radial velocity-based result that a large fraction of ordinary stars in the solar neighborhood are accompanied by a Neptune-or-lower mass planet with an orbital period of 50 days or less.

To get a first idea, I did the following quick (and extremely rough) Monte-Carlo calculation. I took 88,196 stars, and assumed that half of them have a planet with an orbital period drawn uniformly from the 1-d to 50-d orbital range. I then drew the planet masses uniformly from the 1-Earth-mass to 17-Earth-mass range, assumed Neptune-like densities of 1.6 gm/cc, circular orbits, and random orientations. For simplicity, the parent stars’ masses and radii are distributed uniformly from 0.7 to 1.3 times the solar value. I assumed that the 88,196 stars were observed continuously for 33.5 days, and require two transits to appear within the observation interval for a candidate to count. In keeping with the redaction policy, candidates are rejected if their radii were less than 1.5 that of Earth.

The simulation suggests that ~1100 candidate planets should be present in a 88,196 star sample. Encouragingly, this is at least order-of-magnitude agreement, although there’s a hint that the Kepler yield might be lower than what the RV results are implying. It will be very interesting to see what a more careful comparison has to say…

It’s always exciting when the exoplanets rise to the fore of the national discourse.

This morning’s New York Times has a very interesting article about the Kepler Mission’s proprietary data policy. In April, NASA granted the Kepler team an additional window, through February 2011, in which photometry for 400 particularly interesting stars is to be kept out of the public domain.

The article contains all the elements of exoplanetary intrigue that foreshadow traffic spikes for oklo.org in the months ahead. From the P.I., Bill Borucki:

“If I sent you 0’s and 1’s it would be useless… If we say ‘Yes, they are small planets — you can be sure they are.'”

From Ohio State’s Scott Gaudi:

“They need help,” he said, “If they were more open they would be able to get more science out…”

Delicious mention of formal non-disclosure agreements. Big-picture discussions of the meaning of data ownership in the context of federally funded research. 12,000 “suspicious dips” painstakingly distilled to 750 planetary candidates — a near-doubling, in one fell swoop, of the galactic planetary census.

And the oklo.org take? The astronomical enterprise is sometimes an excellent sandbox, a model, for understanding real-world problems. As an interested outsider, I definitely relish the challenges posed by a high-profile data set released under partial duress — a collection of both the ones and the zeroes, where the redactions can speak volumes.

Transit timing variations have a certain allure. Most extrasolar planets are found by patiently visiting and revisiting a star, and the glamour has begun to drain from this enterprise. Inferring, on the other hand, the presence of an unknown body — a “Planet X” — from its subtle deranging influences on the orbit of another, already known, planet is a more cooly cerebral endeavor. Yet to date, the TTV technique has not achieved its promise. The planet census accumulates exclusively via tried and true methods. 455 ± 21 at last count.

Backing a planet out of the perturbations that it induces is an example of an inverse problem. The detection of Neptune in 1846 remains the classic example. In that now increasingly distant age where new planets were headline news, the successful solution of an inverse problem was a secure route to scientific (and material) fame. The first TTV-detected planet won’t generate a chaired position for its discoverer, but it will most certainly be a feather in a cap.

Where inverse problems are concerned, being lucky can be of equal or greater importance than being right. Both Adams’ and Le Verrier’s masses and semi-major axes for Neptune were badly off (Grant 1852). What counted, however, was the fact that they had Neptune’s September 1846 sky position almost exactly right. LeVerrier pinpointed Neptune to an angular distance of only 55 arc-minutes from its true position, that is, to the correct 1/15,600th patch of the entire sky

In the past five years, a literature has been growing in anticipation of the detection of transit timing variations. The first two important papers — this one by Eric Agol and collaborators, and this one by Matt Holman and Norm Murray — came out nearly simultaneously in 2005, and showed that the detection of TTVs will be eminently feasible when the right systems turn up. More recently, a series of articles led by David Nesvorny (here, here, and here) take a direct stab at outlining solution methods for the TTV inverse problem, and illustrate that the degeneracy of solutions, the fly in the ointment for pinpointing Neptune’s orbit, will also be a severe problem when it comes to pinning down the perturbers of transiting planets from transit timing variations alone.

In general, transit timing variations are much stronger and much easier to detect if the unseen perturbing body is in mean-motion resonance with the known transiting planet. In a paper recently submitted to the Astrophysical Journal, Dimitri Veras, Eric Ford and Matthew Payne have carried out a thorough survey of exactly what one can expect for different transiter-perturber configurations, with a focus on systems where the transiting planet is a standard-issue hot Jupiter and the exterior perturber has the mass of the Earth. They show that for systems lying near integer period ratios, tiny changes in the system initial conditions can have huge effects on the amplitude of the resulting TTVs. Here’s one of the key figures from their paper — a map of median TTVs arising from perturbing Earths with various orbital periods and eccentricities:

The crazy-colored detail — which Veras et al. describe as the “flames of resonance” — gives the quite accurate impression that definitive solutions to the TTV inverse problem will not be easy to achieve. One of the conclusions drawn by the Veras et al. paper is that even in favorable cases, one needs to have at least fifty well-measured transits if the perturber is to tracked down via timing measurements alone.

The Kepler Mission holds out the promise of systems in which TTVs will be simultaneously present, well measured, and abundant. In anticipation of real TTV data, Stefano Meschiari has worked hard to update the Systemic Console so that it can be used to get practical solutions to the inverse problem defined by a joint TTV-RV data set. An improved console that can solve the problem is available for download, and a paper describing the method is now on astro-ph. In short, the technique of simulated annealing seems to provide the best route to finding solutions.

A data set with TTVs alone makes for a purer inverse problem, but it looks like it’s going to be generally impractical to characterize a perturber on the basis of photometric data alone. Consider an example from our paper. We generated a fiducial TTV system by migrating a relatively hefty 10 Earth-mass planet deep into 2:1 resonance with a planet assumed to be a twin to HAT-P-7. We then created data sets spanning a full year, and consisting of 166 consecutive measurements, each having 17-second precision, and a relatively modest set of radial velocity measurements. We launched a number of simulated annealing experiments and allowed the parameters of the perturbing planet to float freely.

The resulting solutions to the synthetic data set cluster around configurations where the perturber is in 2:1 resonance (red symbols), and solutions where it is in 3:1 resonance (blue symbols). Furthermore, increasing the precision of the transit timing measurements to 4.3 seconds per transit (solid symbols) does little to break the degeneracy:

The upshot of our paper is that high-quality RV measurements will integral to full characterizations of the planets that generate TTVs. At risk of sounding like a broken record, this means that to extract genuine value, one needs the brightest available stars for transits…