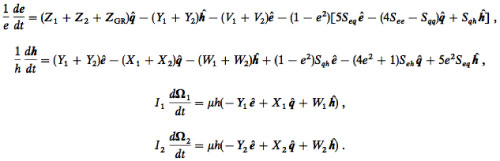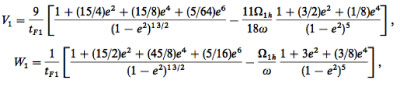
Controversy generates revenue for exoplanet weblogs and supermarket tabloids alike, so I’m always happy when planet-related press releases roll out dramatic, far-reaching claims. Last week’s ESO press release — “Turning Planetary Theory Upside Down” — was quite satisfactory in this regard…
Upon digging into the back story, one finds that the observations underlying the press release are fully uncontroversial — it’s the big-picture interpretation that’s turning heads. Using Doppler velocity measurements taken during transit, Triaud et al. (preprint here) have measured the sky-projected misalignment angles, λ, for six of the transiting planets discovered by the SuperWASP consortium.
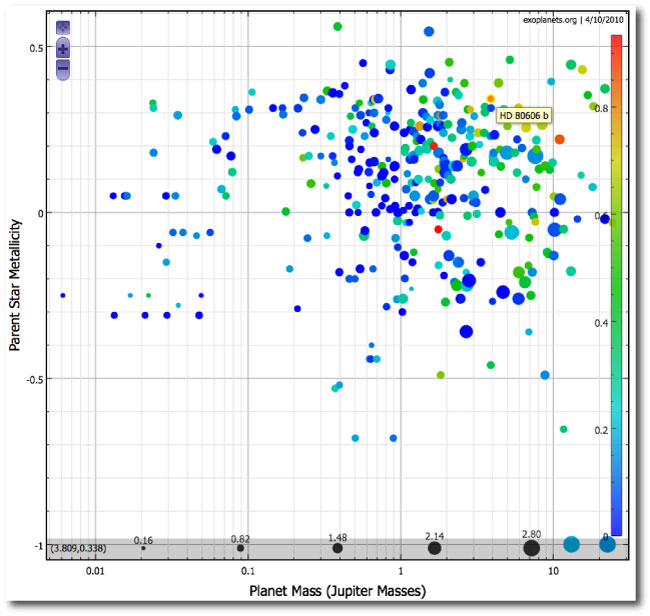
After an initial run of nine transiting planets were found to have sky-projected misalignment angles close to zero, the current count now has 8 out of 26 planets sporting significant misalignment. In the standard paradigm where hot Jupiters form beyond the ice line and migrate inward to reach weekend-length orbits, one would expect that essentially all transiting planets should be more or less aligned with the equators of their parent stars.
The standard migration paradigm, however, leaves at least two questions rather vaguely answered. First, why do the hot Jupiters tend to halt their inward migration just at the brink of disaster? The distribution of orbital periods — slew of selection biases aside — shows a durable peak near ~3 days. Second, why are transiting planets with well-characterized companions so scarce? In general, if one finds a giant planet with a period of ~10 days or more, the odds are excellent that there are further planets to be found in the system. For the known aggregate of transiting planets, and for hot Jupiters in general, additional planets with periods of a few hundred days or less are only infrequently found.

HD 80606b provides a clue that processes other than disk migration might be generating the observed population of hot Jupiters. The planet HD 80606b, its parent star HD 80606, and the binary companion HD 80607 form a “hierarchical triple” system, in which the two large stars provide an unchanging Keplerian orbit that drives the orbital and spin evolution of HD 80606b. If we imagine that HD 80606b and HD 80606 are both subject to small amounts of tidal dissipation, then to plausible approximation, this paper by Eggleton & Kiseleva-Eggleton argues that (i) the orbital evolution of “b”, (ii) the spin vector of “b”, and (iii) the spin vector of HD 80606 itself can be described by a set of coupled first-order ordinary differential equations:
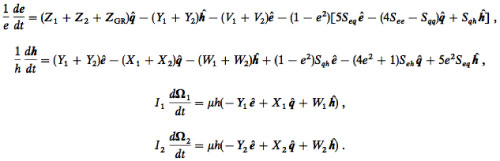
where e and h are vectors describing the planetary orbit, and where Ω_1 and Ω_2 are the spin vectors for HD 80606 and HD 80606b. The equations are somewhat more complicated than they appear at first glance, with expressions such as:
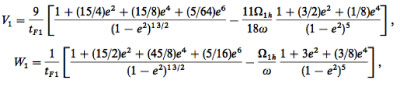
making up the various terms on the right hand sides.
Numerical integrations of the ODEs indicate that solutions exist in which the e and h vectors for `606b are bouncing like a ’64 Impala. Check out, for example, this solution vector animation by Dan Fabrycky (using initial conditions published by Wu and Murray 2003) which shows the leading scenario for how HD 80606b came to occupy its present state.
HD 80606b is imagined to have originally formed in a relatively circular orbit that was roughly 5 AU from its parent star, and which happened to be at nearly a right angle to the plane of the HD 80606-HD80607 binary orbit:
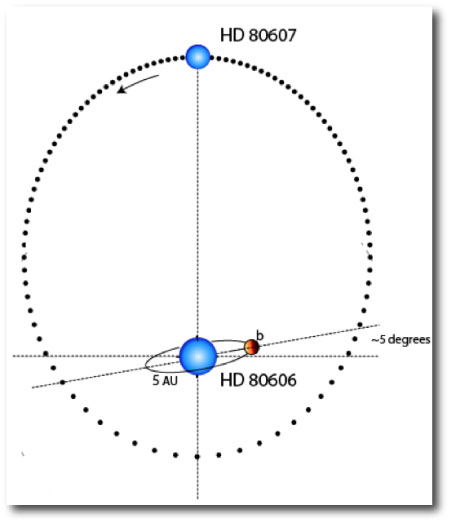
The large mutual inclination led to Kozai oscillations in which ‘606b was cyclically driven to very high eccentricity. During the high-eccentricity phases, tidal dissipation within the planet gradually drained energy from the orbit and decreased the semi-major axis:
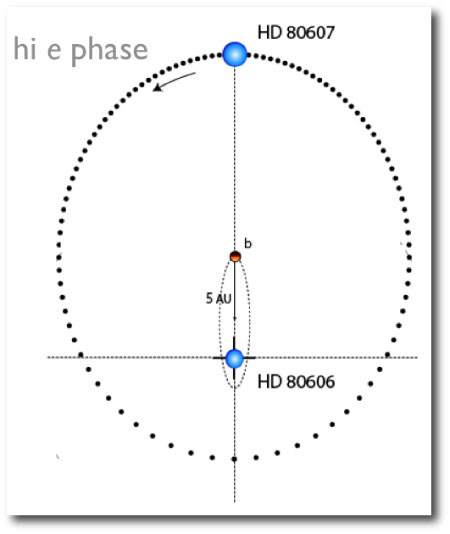
Eventually, the orbital period became short enough so that general relativistic precession was fast enough to destroy the Kozai oscillations, and the planet was marooned on a high-eccentricity, gradually circularizing orbit that is severely misaligned with the stellar equator — exactly what is observed:
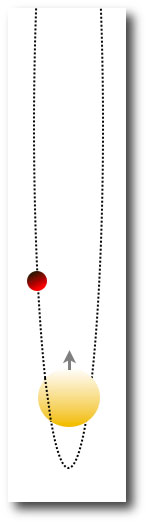
With HD 80606b, the case for Kozai-migration is pretty clear cut. The guilty party — the perturbing binary companion — is sitting right there in the field of view, and the scenario provides an easy explanation for anomalously high orbital orbital eccentricity. The only “just-so” provision is the requirement that the planet-forming protoplanetary disk of HD 80606 started out essentially perpendicular to the orbital plane of its wide binary companion.
The Triaud et al paper and the press release draw the much more dramatic conclusion that Kozai cycles with tidal friction could be the dominant channel for producing of the known hot Jupiters. From the abstract of their paper:
Conclusions. Most hot Jupiters are misaligned, with a large variety of spin-orbit angles. We observe that the histogram of projected obliquities matches closely the theoretical distributions of using Kozai cycles and tidal friction. If these observational facts are confirmed in the future, we may then conclude that most hot Jupiters are formed by this very mechanism without the need to use type I or II migration. At present, type I or II migration alone cannot explain the observations.
Can this really be the case? Might it be time to start reigning in the funding for studies of Type II migration in protostellar disks?
A key point to keep in mind is that Rossiter-McLaughlin measurements yield the sky-projected misalignment angle, λ, between the stellar spin and planetary orbital angular momentum vectors, and not the true misalignment angle, ψ, in three-dimensional space. That is, with transit spectroscopy alone, you can’t discern the difference between the following configurations:
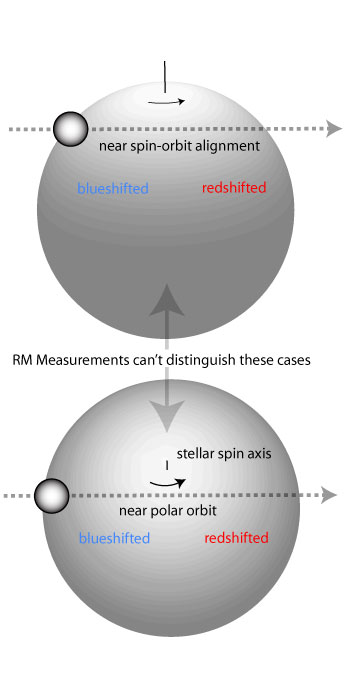
In a paper published in 2007, Dan Fabrycky carried out integrations of the Eggleton-Kiseleva-Eggleton equations for an ensemble of a thousand star-planet-star systems that experience HD80606-style Kozai migration coupled with tidal friction. From the results of the integrations, he constructed a histogram showing the distribution of final misalignment angles, ψ:
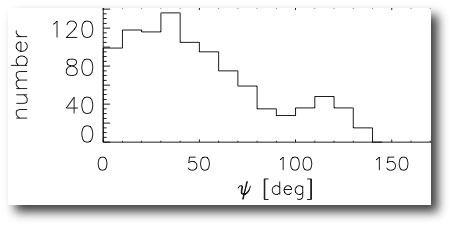
The first nine Rossiter-McLaughlin observations of transiting planets all produced values for λ that were close to zero, in seeming conflict with Fabrycky’s distribution for ψ. The jump-the-gun conclusion, then, was that Kozai-migration is not an important formation channel for hot Jupiters.
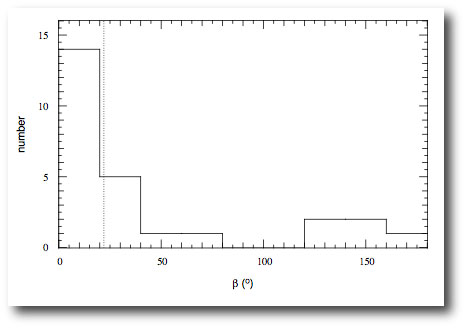
With the spin-orbit determinations that appear in the Triaud et al. paper, there are now a total of 26 λ determinations. A fair fraction of the recent results indicate severely misaligned systems, and Triaud et al. show a histogram over λ (or in their notation, β):
In order to compare the observed distribution of λ measurements with Fabrycky’s predicted distribtion of Kozai-migration misalignments, ψ, Triaud et al. assume that the distribution of spin axes for the transit-bearing stars is isotropic. With this assumption, one can statistically deproject the λ distribution and recast it as a ψ distribution, giving a startlingly good match between Fabrycky’s theory (blue dashed line) and observation:
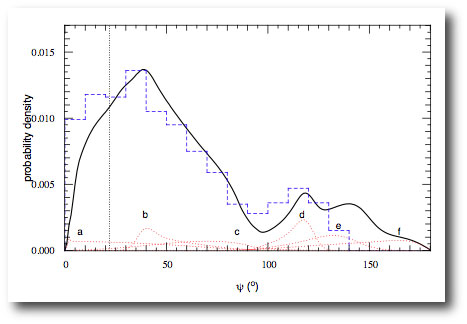
When I first saw the above plot, I had a hard time believing it. The assumption that the spin axes of transit-bearing stars are isotropically distributed seems somewhat akin to baking a result into the data. Nevertheless, it is true that if Kozai migration produces the hot Jupiters, then the current ψ distribution is right in line with expectations.
In early 2009, Fabrycky and Winn did a very careful analysis of the 11 Rossiter measurements that were known at that time. Among those first 11 measurements, only XO-3 displayed a significant sky-projected spin-orbit misalignment. From the sparse data set, Fabrycky and Winn concluded that there were likely 2 separate populations of transit-bearing stars. One population, in which the spins and orbits are all aligned, constitutes (1-f)>64% of systems, whereas a second population, sporting random alignments, is responsible for f<36% of systems (to 95% confidence).
Bottom line conclusion? More Rossiter-McLaughlin measurements are needed, but I think its safe to say that Kozai-migration plays a larger role in sculpting the planet distribution than previously believed. If I had to put down money, I’d bet f=50%.