Monthly Archives: April 2009

Bode’s Law

Posted on by
6

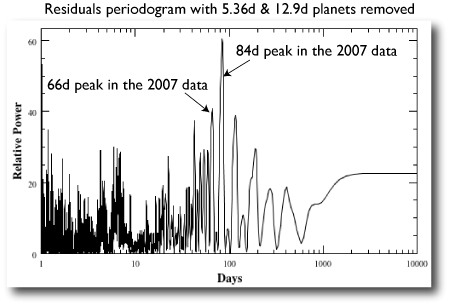
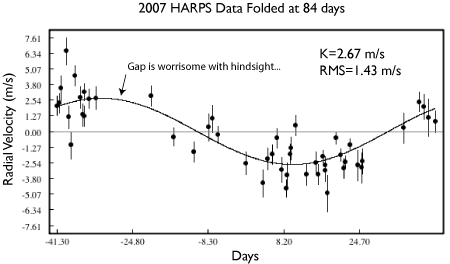
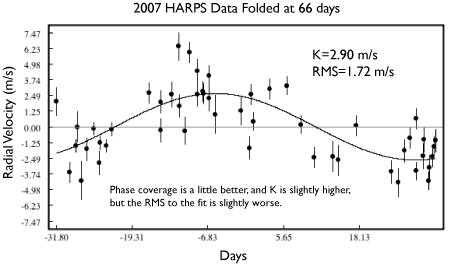
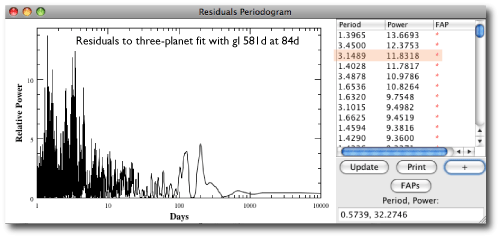
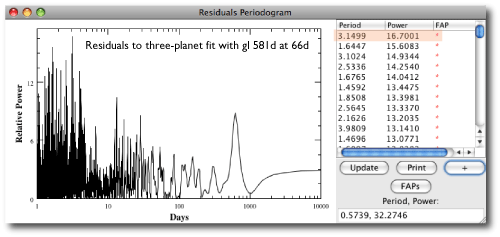
Now I’m certainly not alone in thinking, upon seeing the latest configuration of the Gliese 581 system, Whoa, there’s room for a habitable Earth-mass planet in there…

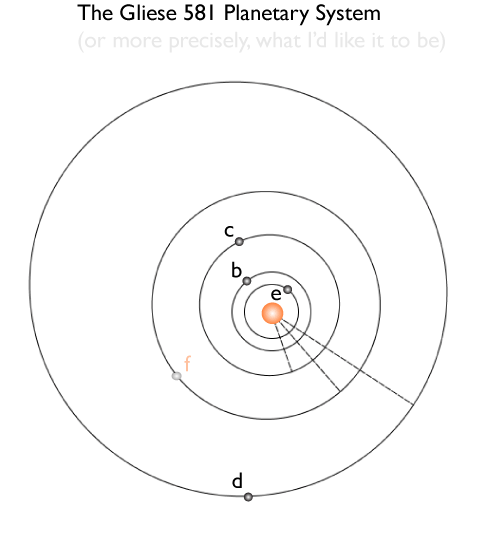
Using the terrestrial planet valuation formula, an Earth-mass planet with a period of 25 days orbiting Gliese 581 is worth 136 million dollars, and needless to say, its detection would be an exciting development. Gliese 581 f seems like such a made-to-order confection that it’s simply got to be there.

Which is a flimsy argument, I admit, but quite frankly, when it comes to Gliese 581, I have no Alpha. I have no idea how and why the Gliese 581 planets wound up with their presently observed properties and configuration. Furthermore, even if one did have a handle on the sequence of events that led to the formation of b,c,d,e and f, and if one wrote that remarkable result up for publication, hardly anyone would believe it. And for good reason. It’s unlikely that the correct blow-by-blow account of what happened in the Gliese 581 protoplanetary disk would lead to any immediately verifiable predictions for any other planetary systems. We’ve observed enough planets now to know that the aggressive nonlinearity of the formation process leads to a bewildering variety of specific outcomes.

It occurred to me that it I might be able to make creatively disingenuous use of Bode’s Law to “predict” the presence of Gliese 581 f at the desired ~25d planetary period. As it stands, Johann Titius pointed out in 1766 that the orbital spacing of the solar system planets is well represented by d=0.4+0.3*(2^i), with i=-Inf, 0, 1, 2, 4, 5, etc. The law worked for Uranus (i=6) and Ceres (i=3), but then famously overperformed by placing a transuranian planet at 38.8 AU. Given that the Titius-Bode relation contains three parameters (a=0.4, b=0.3, and c=2) it’s possible to choose a,b, and c to exactly reproduce Gliese 581 e, b, and c. Unfortunately, the results for d and and f are then rather less than satisfactory, so I decided to abandon a Bode’s law scheme in favor of a straightforwardly bald assertion of Gliese 581 f’s existence.

It’s perhaps for good reason that the Icarus Editorial Office states:

Icarus does not publish papers that provide “improved” versions of Bode’s law, or other numerical relations, unless they are accompanied by some detailed physical/chemical arguments to explain why the new relation is to be preferred.

In the next post, I’ll look in detail at how and when Gliese 581 f can be detected: scenario four.

Aliased

Posted on by
4

Woke up this morning to the startling news that the Geneva team has added an Msin(i)=1.9 Earth mass planet to the Gliese 581 system! The preprint (Mayor et al. 2009) is available from exoplanet.eu, and will appear in Astronomy and Astrophysics. With a radial velocity half-amplitude, K=1.85 m/s, Gl 581e is the lowest-mass planet detected to date.

“The orbital period of the new planet “e” is quite close to pi days. i would mark down a score of -1 for competing planet hunters, whose signals-to-noise are accumulating in proportion to the root of the number of measurements.” said Greg Laughlin, an astronomer at the University of California, Santa Cruz.

In addition to the detection of the new 1.9 Earth-mass planet in the system, the period of Gliese 581d has been revised (to great habitability fanfare) from 84 days to 66 days. Indeed, the new, shorter period raises the habitability value of Gliese 581d from about 0.5 cents to nearly one penny.

As often happens, a strong hint of the new planet was lurking unnoticed in the previously published radial velocity data, and it’s especially interesting to look at the details in this particular case to see how the period revision came about. Let’s work with the 50 radial velocities published by Udry et al. 2007.

The two strongest periodicities in the system come from planets b and c. Removing these planets with the assumption of circular orbits leaves a residuals periodogram that has its strongest peak at 84 days:

The 66 day periodicity is lagging in second place with 66% of the power. Nevertheless, both periodicities provide significant improvement to the fit. An 84-day planet has K=2.67 m/s, and leaves an RMS of 1.43 m/s to the three planet fit:

A best fit 66-day planet has a slightly higher K=2.77 m/s, but leaves an RMS of 1.72 m/s. The chi-square is also higher: 5.10 as compared to 3.65. In the 2007 data, the 84-d planet thus looked quite secure. With hindsight, though, one notices that the phase coverage in the 66-day fit is better than for the 84-day fit. As more data was obtained, it became clear that the 84-day period was an alias of the true 66-day periodicity. Fair enough — RVs are expensive to obtain, and revisions of this sort are an inevitable product of progress.

In the residuals to the fit with the 84-day planet, planet e is present, but it’s masked by a spurious periodicity at 3.45 days,

whereas in the residuals to the fit with the 66-day planet, planet-e is in the #1 spot — not yet significant, but certainly more tantalizing…

Zen++ for film

Posted on by
1

Zen++ for film

Jonathan Langton took the Spitzer 8-micron time-series for HD 80606b and transformed it into a movie of an actual extrasolar planet. The money-minded studio execs, having never seen the the successful prequel, decided that the full 30-hour version might not do well in theaters, so the original “Director’s Cut” had to be edited. The final result? Thirty hours of one-pixel, gray-scale footage have been compressed into a 10-second movie showing the excitement surrounding perihelion at a rate of 3 hours per second.

Be sure to watch for the secondary eclipse!