Monthly Archives: February 2008

Toward Alpha Cen B b

Posted on by
25

Image Source.

Yesterday, I gave a talk at the JPL Exoplanet Science and Technology Fair, a one-day meeting that showcased the remarkably broad variety of extrasolar planet-related research being carried out at JPL. In keeping with the wide array of projects, the agenda was fast-paced and completely diverse, with talks on theory, observation, instrumentation, and mission planning.

The moment I walked into the auditorium, I was struck by the out-there title on one of the posters: The Ultimate Project: 500 Years Until Phase E, from Sven Grenander and Steve Kilston. Their poster (pdf version here) gives a thumbnail sketch of how a bona-fide journey to a nearby habitable planet might be accomplished. The audacious basic stats include: 1 million travelers, 100 million ton vessel, USD 50 trillion, and a launch date of 2500 CE.

Fifty trillion dollars, which is roughly equivalent to one year of the World GDP, seems surprisingly, perhaps even alarmingly cheap. The Ultimate Project has a website, and for always-current perspective on interstellar travel, it pays to read Paul Gilster’s Centauri Dreams weblog.

Interest in interstellar travel would ramp up if a truly Earth-like world were discovered around one of the Sun’s nearest stellar neighbors. Alpha Centauri, 4.36 light years distant, has the unique allure. Last year, I wrote a series of posts [1, 2, 3, 4] that explored the possibility that a habitable world might be orbiting Alpha Centauri B. In short, the current best-guess theory for planet formation predicts that there should be terrestrial planets orbiting both stars in the Alpha Cen binary. In the absence of non-gaussian stellar radial velocity noise sources, these planets would be straightforward to detect with a dedicated telescope capable of 3 m/s velocity precision.

Over the past year, we’ve done a detailed study that fleshes out the ideas in those original oklo posts. The work was led by UCSC graduate student Javiera Guedes and includes Eugenio, Erica Davis, myself, Elisa Quintana and Debra Fischer as co-authors. We’ve just had a paper accepted by the Astrophysical Journal that describes the research. Javiera will be posting the article to astro-ph in the next day or so, but in the meantime, here is a .pdf version.

Here’s a diagram that shows the sorts of planetary systems one should expect around Alpha Cen B. The higher metallicity of the star in comparison to the Sun leads to terrestrial planets that are somewhat more massive.

We’re envisioning an all-out Doppler RV campaign on the Alpha Cen System. If the stars present gaussian noise, then with 3 m/s, one can expect a very strong detection after collecting data for five years:

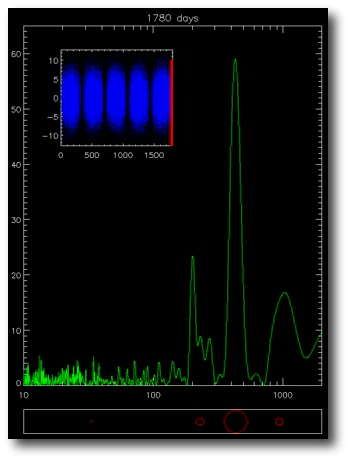
Here’s a link to an animation on Javiera’s project website which shows how a habitable planet can literally jump out of the periodogram.

I think the planets are there. The main question in my opinion is whether the stellar noise spectrum is sufficiently Gaussian. It’s worth a try to have a look…

two for one deals?

Posted on by
5

Image Source.

The Gliese 876 system is remarkable for a number of reasons. It makes a mockery of the notion that the minimum-mass solar nebula has a universal validity. It harbors one of the lowest-mass extrasolar planets known (discovered by our own Eugenio Rivera). And of course, the outer two planets are famously caught in a 2:1 mean motion resonance, in which the inner 0.8 Jupiter-mass planet makes (on average) exactly two trips around the red dwarf for every one trip made by the outer 2.5 Jupiter-mass planet.

As users of the console know, the planet-planet interactions between the Gliese 876 planets are strong enough so that one needs a self-consistent dynamical fit to the system. Even on the timescale of a single outer planet orbit, the failure of the Keplerian model can be seen on a 450-pixel wide .gif image:

The following three frames are from a time-lapse .mpg animation of the Gliese 876 system over a period of roughly one hundred years:


Each frame strobes the orbital motion of the planets at 50 equally spaced intervals which subdivide the P~60 day period of the outer planet. Upon watching the movie, it’s clear that the apsidal lines of the outer two planets are swinging back and forth like a pendulum. This oscillation has an amplitude (or libration width) of 29 degrees, and acts like a fingerprint identifier of the Gliese 876 system.

The derangement of the orbits is reflected in their continual inability to maintain an exact 2:1 orbital commensurability. The first figure up above shows that when planet c has finished exactly two orbits, it has already managed to lap planet b, which was still dawdling down Boardwalk prior to passing GO.

Planet b, however, doesn’t always run slow. The gravitational perturbations between the two planets provide a second pendulum-like restoring action which prevents the bodies from straying from the average period ratio of 2:1, which, over the long term, is maintained exactly. The degree to which the orbits themselves librate, combined with the planets’ abilities to run either ahead or behind exact commensurability is captured by the resonant arguments of the configuration. These can be defined as,

where the lambdas are mean longitudes and the curly pi’s are the longitudes of periastron. The two resonant arguments capture the simultaneous libration of the mean motions and the apsidal lines. The smaller the arguments, the more tightly the system is in resonance.

In the Gliese 876 system, the resonant arguments are both librating with amplitudes of less than 30 degrees. This is evidence that a dissipative mechanism was at work during the formation of the system. Interestingly, however, when one looks at the other extrasolar planetary systems that are thought to be in 2:1 resonance, one finds that the libration amplitudes in every case are much larger. In fact, in the HD 73526 system and in the HD 128311 system, only one of the arguments is librating, while the other is circulating. In this state of affairs, the apsidal lines act like a pendulum that is swinging over the top. In addition, the orbital eccentricites are higher, and the sum of planet-planet activity is strikingly greater (see this animation of the evolution of the HD 128311 system).

A gas disk seems to be the most likely mechanism for pushing a planetary system into mean-motion resonance. Protoplanetary disks are likely, however to experience turbulent density fluctuations. These density fluctuations lead to stochastic gravitational torques, which provide a steady source of orbital perturbations to any planets that are embedded in a disk. For a reasonable spectrum of turbulent fluctuations, it turns out that it’s rather difficult to wind up with a planetary system that is as deeply in resonance as Gliese 876. The conclusion, then, is that Gliese 876-like configurations should be quite rare. Indeed, 2:1 resonances of every stripe should constitute only a minor fraction of planetary systems, and the majority that do exist should either large libration widths or only a single argument in resonance.

If you’re interested in more detail, we’ve submitted a paper that goes into much more detail (Adams, Laughlin & Bloch, ApJ, 2008 Submitted).