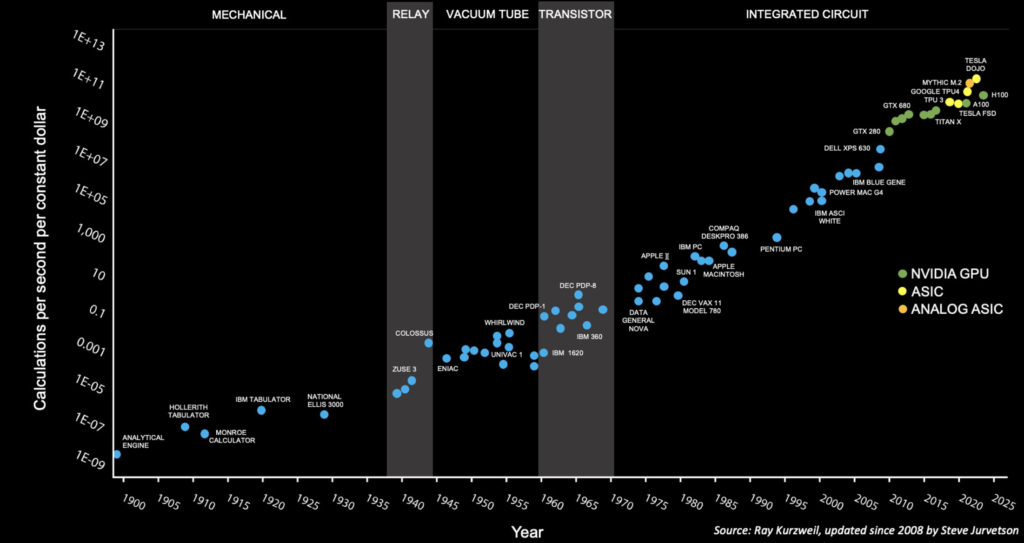
I’ve likely already gone on in these pages about how, consistently, year in and year out, my success rate with hypotheses, with theoretical ideas, runs right at about one percent. “Getting cured”, as they say in the oil patch, will thus require a lot of drilling.
I reminisce with some nostalgia back to the first hypothesis that I can count as a credible idea. In February 1989, an article was published in Nature describing the unambiguous detection of a new pulsar at the exact location of Supernova 1987a in the Large Magellanic Cloud. Shining at 18th magnitude, the freshly squeezed neutron star was consistently detected in optical light over the course of a seven-hour observation, and amazingly, the pulse rate was clocked at nearly 2000 times per second. The signal varied sinusoidally during the course of the night, moreover, in a matter that suggested that a Jupiter-mass object could be orbiting a mere million kilometers above the surface of the newborn neutron star. I still have a faded-toner xerox of the article, covered with scribbled notes and feverish florescent highlighter underscores.
By fortuitous coincidence, when the pulsar discovery was announced, I was enrolled in Stan Woosley’s graduate course on the evolution of massive stars, and so I could feel a tangible excitement, a thrilling shade of cousin-once-removed connection to real scientific action.
And mysteriously, after the initial night of observation, there was zero further sign of the pulsar. Independent groups of observers searched for it and could not find it. Perhaps, went the conventional best guess, perhaps it had been caught shining through a lucky transient window in the debris from the explosion? Or perhaps (and I believe this was Stan’s take) it was an artifact of the detector?
Naw. Those suggestions seemed hopelessly pedestrian. They lacked imagination. Clearly, if an article had been published in Nature, then the observers knew what they were doing. The possibility of error seemed entirely remote. I was seized by the fact that a neutron star spinning at 2000 times per second would be rotating at very close to its breakup velocity. Moreover, that possible Jupiter-mass companion could be the product of a fission event in a proto-neutron star that was born spinning too fast. My mind raced. A fission event would leave the larger remnant spinning very close to breakup, Maybe the resulting primary object it was right at the limit of the maximum neutron star mass. Maybe in the weeks following the one-night observation, it had shed enough angular momentum via gravitational radiation so that the the centrifugal pressure from rotation was no longer sufficient to provide support the object against its self-gravity. I had it! The neutron star was no longer radiating because it was no longer there… it had collapsed into a black hole!
I dove headlong into the theory of the neutron star equation of state. I was neither equipped nor qualified to understand the details of the literature, but it was possible to shard off some order-of-magnitude rules of thumb. I showed my formula-scribbled sheets to Stan, “This has got to be it!”
I have to say, Stan handled it just right — no patronizing over-praise, but also no outright dismissal. I think his words were something to the effect that every theorist is allowed one wild idea (but not two).
Fast-forwarding to February 1991, my focus had shifted almost entirely to trying to front a Skinny-Puppy style dance-Industrial band, and I was barely even attending to my studies. I don’t think I was even aware of the discovery that that pulsar signal was, in actuality, just a subtly shifting flicker from the closed-circuit television camera attached to the Cassegrain focus of the four-meter telescope at the Cerro Tololo lnteramerican Observatory.