
Douglas Adams single-handedly elevated the number 42 to a prominence that it otherwise certainly wouldn’t have.
Not that the atomic number of molybdenum should lack importance. Forty two, moreover (and change) is the number of minutes required to fall through a uniform density Earth in the event that a frictionless shaft were to be somehow dug through the globe.
The issue of falling through the Earth naturally proceeds to the antipodal map. That is, where do you come out if you tunnel vertically?
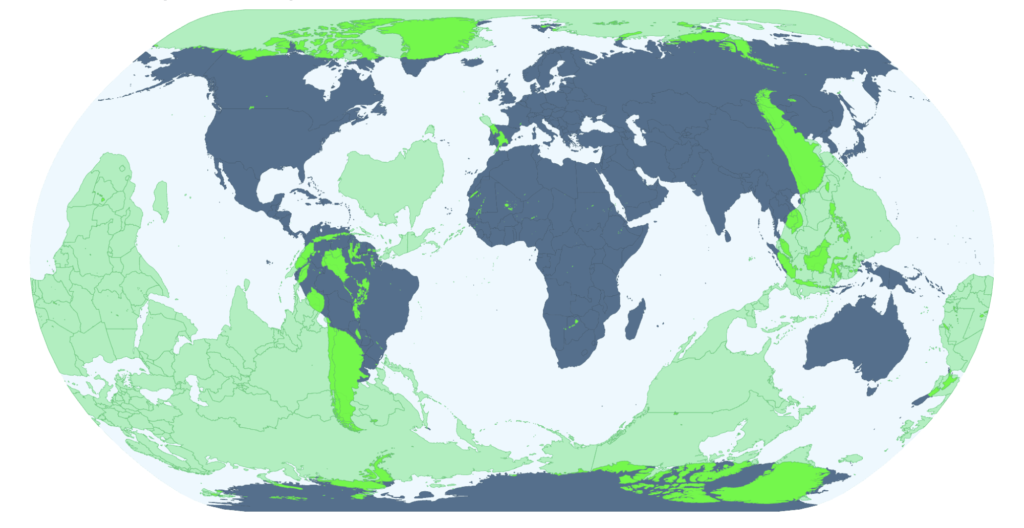
If you’re reading this in North America, you come out in the Indian Ocean, hundreds to thousands of miles from Perth Australia, the nearest big city. The one exception is locations just north of the Sweet Grass Hills of Montana:

which are antipodal to Kerguelen:

In fact, if you’re reading this on land anywhere on Earth, your odds of not emerging in the ocean are rather slim. Only three percent of the globe is comprised of land that is antipodal to land. In essence, the cone of South America runs through China into Siberia on the antipodal map.
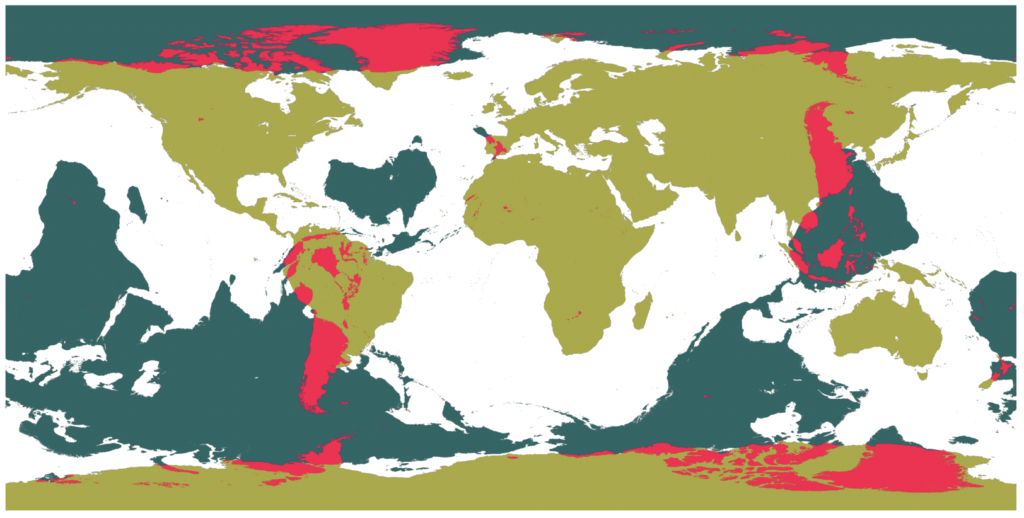
Staring at the map reveals some curious asymmetries. Look at how Australia nestles into the Atlantic, and how Africa fits into the Pacific. Is this just a random superposition? On average we’d expect three times as much land to be antipodal to land than is the case with the present-day Earth. Is this a “thing”, or is it simply a coincidence?
The andecdotal land-opposite-ocean observation can be analyzed by decomposing the Earth’s topography into spherical harmonics and analyzing the resulting power spectrum. In 2014, I wrote an oklo.org article that looked at this in detail. Mathematically, the antipodal anticorrelation — the tendency of topographical high points to lie opposite from topographical low points — is equivalent to the statement that the topographical power spectrum is dominated by odd-l spherical harmonics.
Arthur Adams and I have been looking into the antipodal anti-correlation off and on for a number of years, and have worked up some theories that are almost certainly incorrect (as are essentially all theories that involve and then in their initial construction). Nonetheless, they are provocative and polarizing, and so thus appropriate to the jaded sensibilities of oklo.org’s sparse readership of scientific connoisseurs.
To start, the antipodal anti-correlation has been around at least since the Carboniferous. Paleo digital elevation models exist, and so we can look at the evolution of the topographical power spectrum through time:


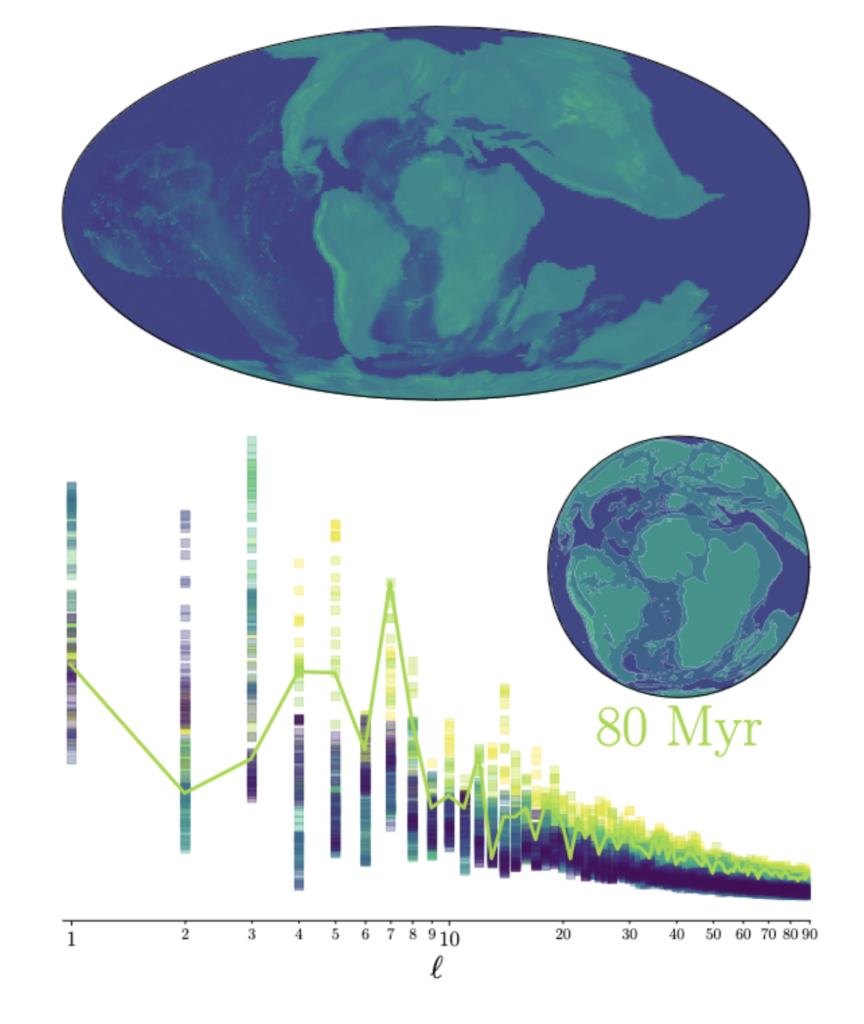
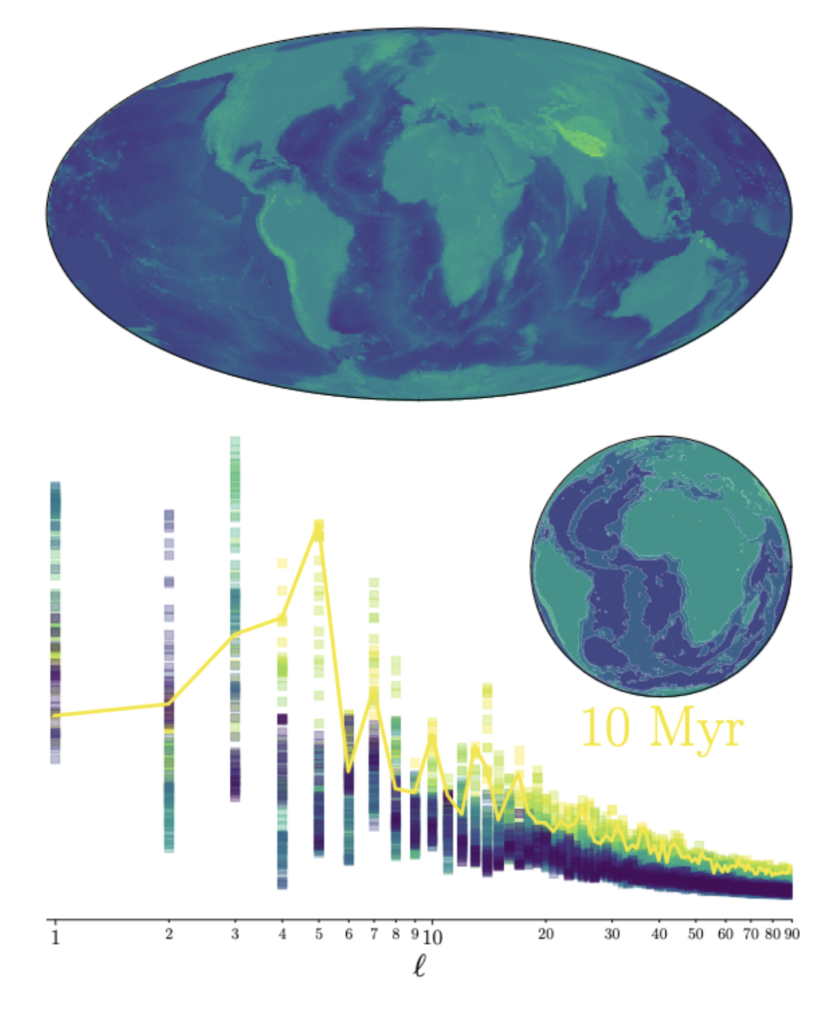

Since roughly 330 million years ago, when the super-continent Pangaea first assembled, the elevation spectrum has exhibited strong powers in the l = 1 harmonic (peaking about 320 million years ago), at the l = 3 harmonic (peaking about 180 million years ago), at the l = 7 harmonic (peaking about 80 million years ago), and most recently at the l = 5 harmonic, which peaked about 10 million years ago and which continues to the present day. The current net anti-correlation is actually near its minimum strength relative to the last few hundred million years of Earth’s history. Is there a physical reason for this marked preference for odd-l modes?
