Last August, SFMOMA put on an exhibition that featured a number of Chuck Close’s hyperrealistic portraits. It was interesting to study the sudden transition between a patchwork of acrylic brush strokes, as in the cell-phone close-up snapshot just above, and an image that makes sense as a whole.

The recent public release of the Kepler data triggers an effect that’s a bit like stepping back rapidly from one of Close’s portraits. Suddenly, a huge swath of the planetary distribution connects with a larger picture. This effect holds especially true when one looks at the list of systems that harbor multiple transiting candidates.

With the census of radial velocity planets, it’s often quite difficult to determine whether a signal is originating from a single planet on an eccentric orbit, or a pair of planets participating in 2:1 resonance. The only really well-characterized unambiguously resonant RV system is Gliese 876, where the combination of large Ks, a long observational base, and rapidly unfolding 30-60-120d orbits has allowed the dynamics of the resonance to be revealed in detail.

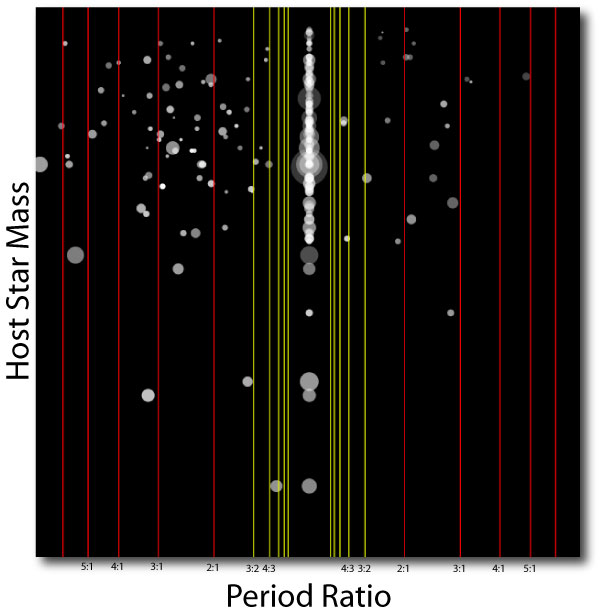
The 115 Kepler two-transit systems indicate right away that systems like Gliese 876 are intrinsically rather rare. In the illustration below, I’ve taken each of the two-transit systems, and identified the larger member of the pair. I’ve then plotted the period ratio, P_small/P_large as the x coordinate, the parent star’s mass as the y coordinate, the temperature of the planets as a grayscale (saturating to white at 1500K), and the sizes of the symbols in proportion to the observed radii.

The immediate impression from the diagram is that the systems are not overwhelmingly clustered around the simple integer commensurabilities. Low-order mean-motion resonances among the extrasolar planets are the mild exception, and not the rule.

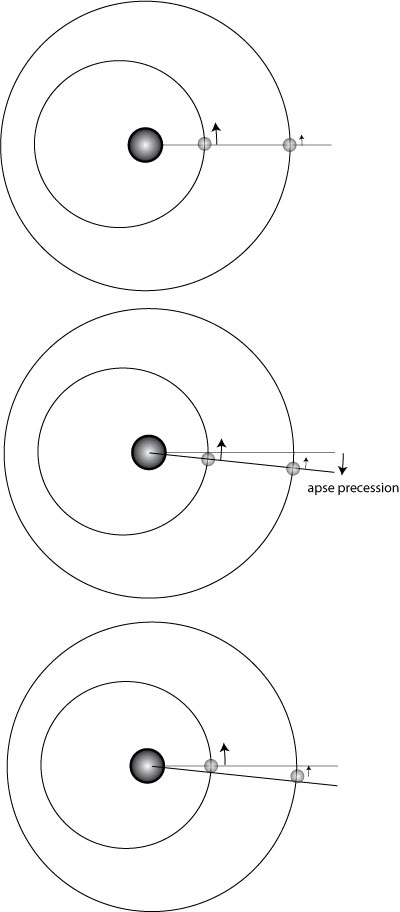
That said, the resonant systems are clearly present. Of the forty 2-transit systems with inner-outer period ratios lying between 2.0 and 3.0, six of them have period ratios between 2.02 and 2.05. The chances of a concentration like this occurring purely by chance is considerably less than 1%. Furthermore, the fact that the clustering occurs a percent or two above the exact 2:1 commensurability can be understood in terms of the dynamics of resonance. When one has two massive planets deep in a resonance, with a significant angular momentum deficit, then the system apse precesses in a retrograde direction (as is the case with Gliese 876). The resonance is controlled by a restoring force that drives conjunctions to occur at periastron. This means that if one observes along a fixed line of sight, then the inner planet is seen to orbit a bit more than two times as often as the outer planet.