
It’s been rather arduous past few days as the HST Cycle-18 proposal deadline — 5 PM PST, Friday Feb. 26th, to be exact — bore down like a freight train.
During the past year, I’ve become quite intrigued by the remarkable (and well known) HST observation by Vidal Madjar et al. (2003), who discovered that the Lyman-alpha transit depth of HD 209458b is a whopping 15% (as opposed to the mere 1.5% of the star’s light that gets blocked during the optical transit). The implication of this result is that the planet is surrounded by an outflowing, escaping wind of hydrogen, and the discovery has sparked a lot of theoretical work.
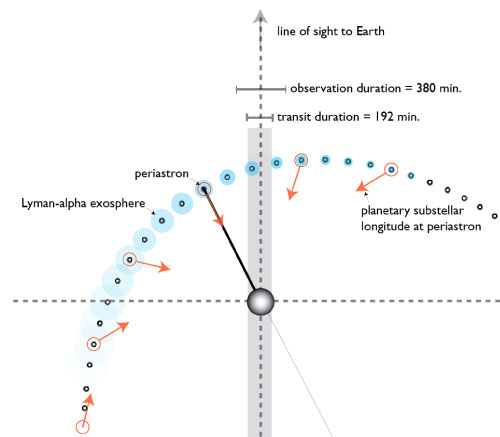
A good test for planetary outflow hypotheses is to see what they predict for eccentric planets that undergo drastic changes in stellar heating during the course of the orbit. Fred Adams and I have been working on hydrodynamical models for these situations, and it soon became clear that oklo.org fave HD 17156b, the P=21.2d, e=0.67 transiting planet provides an intriguing observational opportunity for HST/STIS. HD 17156 is currently the fourth-brightest known parent star of a transiting extrasolar planet (after HD 209458, HD 189733 and HD 149026) and it lies in HST’s so-called continuous viewing zone for part of the year. This means that a full transit can be observed without having to take those leisurely once-per-96-minute pit stops every time Earth blocks the view.
The geometry of the transit, furthermore, is such that the planet is getting its maximum sunburn just a few hours after transit egress. Our calculations indicate that it should take the upper atmosphere only a matter of hours to react to the increased heating, so we’re optimistic about the possibility that not only will HST detect a deep transit in the UV, but that it might even be able to detect the Lyman-alpha transit depth increasing during the course of the transit. Here’s the basic idea:
As of a few minutes ago, the proposal was received safe and sound at STScI, so now it’s time to kick back, wait, and see if it passes muster with the TAC…

Wow, that is fascinating to think about it.
What can we expect for a transit light curve shape?
Would I be correct in expecting that the time between the exosphere transit and the planet transit would be less on the ingress than it would be on egress? And can we expect a more ‘slanted’ transit light curve as the exosphere expands during the transit itself?
To clarify: would the (exosphere’s first contact – the planet’s first contact) be < (exosphere's fourth contact – planet's fourth contact)?