As the decade draws to a close, it’s hard not to be amazed at the progress that’s been made on every research front related to extrasolar planets.

An area that I think is now ripe for progress comprises coordinated multi-observer checks for transits by super-Earth/sub-Neptune planets. There are now over thirty known extrasolar planets with Msin(i)’s less than that of Gliese 436b (which tips the scales at 23 Earth masses). Of these, only CoRoT-7b has so far been observed to transit, and it’s very probable that the current catalog of low-mass RV-detected planets contains one or more transiting members. Needless to say, it’d be very interesting to locate them.

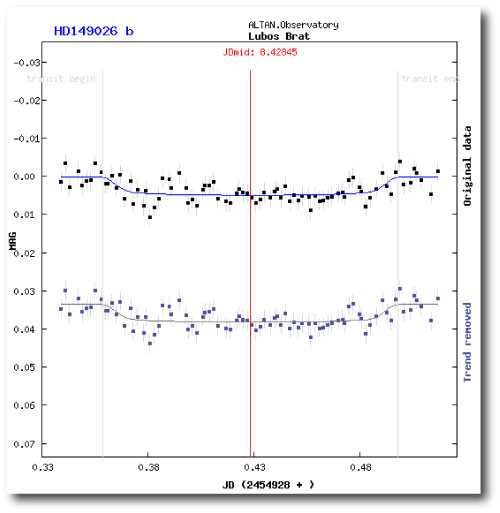
To my knowledge, the lowest-amplitude transits that have been observed by amateur astronomers have been those by HD 149026b. This anomalously dense Saturn-mass planet induces a photometric transit depth of roughly 0.4%.  State-of-the-art amateur detections show the transit very clearly. Here’s an example (the observer was Luboš Brát of the Czech Republic) taken from the TRESCA database:

The identification of transits by small planets certainly won’t be a picnic. Super-Earths and  sub-Neptunes orbiting G and K stars present targets that are intrinsically much tougher than HD 149026. Unless the parent star is a red dwarf, the expected transit depths will generally be less than 0.1%, and it’ll be extremely difficult for a single small-telescope observer to obtain a definitive result.

On the other hand, if a platoon of experienced observers mount a coordinated campaign on a single star, then there’s a possibility that a startlingly good composite light curve might be obtained. In theory, if one were to combine the results from sixteen independent observers, one could obtain a light curve of the equal signal-to-noise as the HD 149026b curve shown above, but for a planet with a transit depth of only 0.1%.

I spent time this weekend making sure that the transitsearch.org transit predictions for the known RV-detected low-mass planets are as up-to-date and accurate as possible. I found that HD 7924 is a good candidate star with which to test a coordinated observing strategy. The star harbors a low-mass RV-detected planet was announced earlier this year (discovery paper here):

HD 7924b has Msin(i)~10 Earth Masses, a P=5.3978d orbital period, and a 6.7% a-priori chance of being observable in transit. The (folded) photometry in the discovery paper is of quite high quality, and shows that the star is not photometrically variable. The photometry also indicates that transits with depth greater than 0.05% are probably not occurring. The parent star, HD 7924 is a K-dwarf, with a radius of something like 78% that of the Sun, which means that if the planet is a sub-Neptune it’ll have a central transit depth of order 0.075%, whereas if it is a rocky object, the depth will likely be less than 0.05%. The 1-sigma uncertainty on the time of the transit midpoint is about 0.35 days. The parent star has V=7.2, and with Dec=+76 deg, it’s circumpolar for high-latitude observers (RA=01h 21m).

Here are the next predicted transit midpoints (dates and times are UT):

HJD        Y    M  D  H  M
2455182.04 2009 12 16 12 51
2455187.01 2009 12 21 12 14
2455192.41 2009 12 26 21 48
2455197.81 2010  1  1  7 21
2455203.20 2010  1  6 16 54
2455208.60 2010  1 12  2 28

Because HD 7924b’s period is known to an accuracy of 0.0013 days (2 minutes), participating Northern-hemisphere observers can obtain data during any of the upcoming opportunities. Their light curves, once standardized, can in theory be stacked to obtain increased precision. It would be very interesting to get a sense of the practical limits inherent in such an approach. I think the best way to test the limits is to give the observations a try!