
Image Source.
The range of planetary orbits that are observed in the wild is quite a bit more varied than the staid e < 0.20 near-ellipses in our own solar system. For regular oklo readers, the mere mention of Gl 876, 55 Cancri, or HD 80606, is enough to bring to mind exotic worlds on exotic orbits.
Non-conventional configurations involving trojan planets have been getting some attention recently from the cognescenti. Even hipper, however, is a configuration that I’ll call the 1:1 eccentric resonance. Two planets initially have orbits with the same semi-major axis, but with very different eccentricities. Conjunctions initially occur close to the moment of apoastron and periastron for the eccentric member of the pair.
Here’s a movie (624 kB Mpeg) of two Jupiter-mass planets participating in this dynamical configuration.
At first glance, the system doesn’t look like it’ll last very long. Remarkably, however, it’s completely stable. Over the course of a 400-year cycle, the two planets trade their angular momentum deficit back and forth like a hot potato and manage to orbit endlessly without anyone getting hurt.

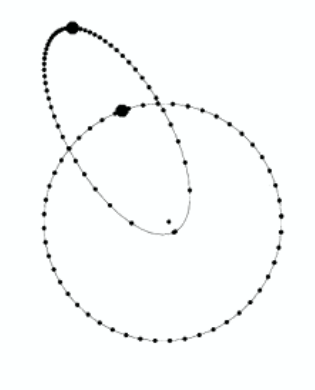
Here’s an animation (1 MB Mpeg) which shows a full secular cycle. The red and the blue dots show the planet positions during the two orbit crossings per orbit made by one of the planets. It’s utterly bizarre.
These animations were made several years ago by UCSC grad student Greg Novak (who’ll be getting his PhD this coming summer with a thesis on numerical simulations of galaxy formation and evolution). As soon as we can get the time, Greg and I are planning to finish up a long-dormant paper that explores the 1:1 eccentric resonance in detail. In short, these configurations might be more than just a curiosity. When planetary systems having three or more planets go unstable, two of the survivors can sometimes find themselves caught in the 1:1 eccentric resonance. The radial velocity signature of the resulting configuration is eminently detectable if the planets can be observed over a significant number of orbital periods.

Taking a look at the behaviour of the 1:1 solutions for the HD 128311 and HD 82943 systems proposed by Goździewski and Konacki, they seem to be doing a similar kind of thing (but with mutual inclination being involved in all the fun as well).
Incidentally, what does this configuration look like in a rotating reference frame? Is it any different from a quasisatellite?
Hi Andy,
If memory serves, I think that the Gozdziewski and Konacki solutions are indeed a specific example of the 1:1 eccentric resonance. There’s a huge variety of available configurations once mutual inclination is allowed. It would be interesting to watch them vibrate in 3D over secular time scales.
In the rotating reference frame, one sees that the 1:1 resonance is indeed a retrograde quasi-satellite.
best,
Greg