
Regular oklo readers all know that HD 209458 b is a lot bigger than it’s supposed to be.
In a previous post, we saw that the theoretical models that provide reasonable matches for the other 9 transiting planets predict that HD 209458 b’s radius should be slightly larger than Jupiter’s radius. The observations, on the other hand, make it clear that the planet is actually has a diameter about 1.35 times larger than Jupiter. HD 209458 b is by far the best-studied exoplanet, so it’s of more than passing interest to understand why it’s so large.
There’s general agreement that HD 209458 b must be privately tapping an unusual source of internal heat. Somehow, a lot of extra energy is being generated in the planetary interior. The surplus heat allows the planet to maintain an expanded outer envelope, and hence endows the planet with a larger overall size. The big question is: what is the anomalous extra heat source? A few years ago, I was enthusiastic about the idea that there might be a second companion planet that is gravitationally perturbing HD 209458 b, forcing it to maintain a slightly eccentric orbit. This eccentricity would be continually damped as a result of tidal interactions with the parent star, which would generate a sufficient amount of interior heating. Such a state of affairs is analogous to the heating of the inner Jovian satellites. The heat generated by tidal friction lends Io its off-the-hook volcanism, and maintains Europa as the Astrobiology poster world.
Unfortunately, however, the perturbing companion model no longer seems to be a viable explanation of HD 209458 b’s large size. That is, if you use the systemic console to fit to the HD 209458 b radial velocities, you’ll find that there is very little latitude for inserting significant extra planets. Try it and see, and upload your fits to the systemic back-end.
Josh Winn (MIT) and Matthew Holman (Harvard-Smithsonian CfA) have written a paper that presents an interesting hypothesis for resolving the HD 209458 b radius dilemma. Winn and Holman propose that the planet is caught in a so-called Cassini state, which is a resonance between spin precession and orbital precession. In a future post, I’ll give a heuristic discussion of the dynamics of how this situation can arise, and how the Cassini states work, but in short, if HD 209458b is trapped in the “Cassini state 2”, then its spin axis will lie almost in the orbital plane. Like all hot Jupiters, the planet will spin once per orbit, but it will literally be lying on its side as it orbits the parent star. A synchronous planet in Cassini state 2 will experience a large amount of tidal heating, even in the complete absence of any other planets in the system.
I like the Winn-Holman hypothesis because it’s potentially testable. If the planet is in Cassini state 2, then the pattern of illumination on the surface, and hence the time-dependant global infrared signature, will be very different than if it is locked into the standard upright configuration. In the standard scenario, a hot Jupiter has a fixed substellar point on its equator that does not wander significantly as the planet executes its orbit. One hemisphere of the planet is in perpetual day, while the other hemisphere experiences an endless night. Hydrodynamic calculations by James Cho and his collaborators (link), and by Adam Showman and his students (link), suggest that hot Jupiters should have a single strong equatorial jet that advects heat from the hot dayside to the cool night side. The oklo splash image has been adapted from Cho’s calculations, and shows this jet in action (see this post for more discussion).
I’ve been advising UCSC Physics graduate student Jonathan Langton, who has recently begun a study of what the flow pattern on a hot Jupiter should look like if the planet is caught in Cassini state 2. If the planet’s rotation axis lies in the orbital plane, and if the planet spins on its axis once per orbit, then the play of light and shadow across the planetary orb has a pattern that is totally unlike our seasons here on Earth. At the north and south poles, of a spin-synchronous Cassini-state-2 planet, the parent star rises, passes directly overhead, and then sets once per orbit. At one special spot on the equator, on the other hand, the star is always visible, and additionally passes directly overhead once per orbit. At the opposite spot on the equator (which we’ll call the anti-stellar point), the star never fully rises, but rather peeks half of its diameter above opposite horizons once per orbit.

Jonathan has made two short .avi format animations that help to illustrate the situation. In the first animation, we hover above the point on the equator that receives maximum illumination. In the second animation, we hover above the point on the equator that receives the least illumination. The mythology on such a world would likely be pretty interesting.
When a spin-synchronous planet is illuminated in this bizarre manner, the flow pattern on its surface should be very different than the flow pattern that would occur if the planet is in the standard upright configuration. Jonathan has finished a preliminary set of simulations using the so-called shallow water approximation which indicate that this is indeed the case. (The shallow water approximation is a 2-dimensional method for simulating atmospheric dynamics on the surface of the planet under the assumption that the depth of the fluid is much smaller than the horizontal scales of interest. Use of this approximation doesn’t require us to assume that the red-hot Jupiter is actually covered with water!)
Here are two of Jonathan’s .avi format animations that show the (still very) preliminary results. The first animation [11 MB, modem users watch out!] shows the evolution of the temperature distribution (on the anti-stellar hemisphere) for a planet in Cassini state 2. Here’s a snapshot at a particular moment in time:
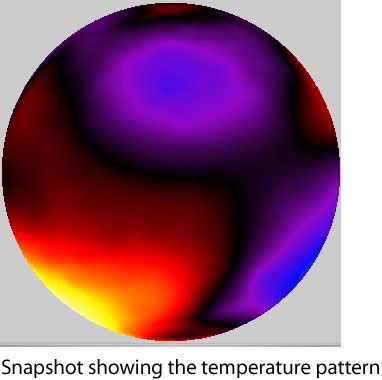
The second animation [12 MB] shows the distribution of vorticity across the planet surface. The vorticity at a particular spot in a fluid flow can be thought of as the ability of the flow to cause a tiny imaginary paddle-wheel to spin. Here’s a snapshot from the animation. The high-vorticity orange structure is a giant fiery hurricane-like storm on the surface of the planet:
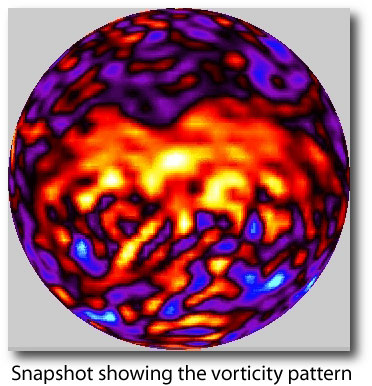

So the planet doesn’t have any bands or jets, but instead has a giant cyclone? Is the vorticity pattern also for the antistellar hemisphere, and what does it look like on the substellar one?
BTW the link to the vorticity animation should be http://www.oklo.org/wp-content/images/eta200_10_20vort.avi
Andy,
Yes, that is our preliminary interpretation of the results. They’re currently being run at higher resolution to verify the conclusion. The vorticity animation hovers above the substellar hemisphere. The antistellar hemisphere point of view looks pretty similar, since the vortex seems to be traveling around the planet.
Thanks for noticing the incorrect link. Should be fixed now.
best,
Greg
As I recall, a plot of average longitudinal velocity as a function of latitude showed ~3 zonal jets, in good qualitative agreement with Cho et al [2003]. Also, it’s not immediately obvious to me that the jets will necessarily show up on the vorticity pattern.
The entire configuration seems to revolve around the planet with a period of ~3 days, so that there’s not a lot of difference here between the substellar and anti-stellar hemispheres. In this case, we were using fairly weak forcing and a fairly long radiative equilibrium time, so that’s perhaps not unexpected.
Pingback: systemic - flowchart
Pingback: systemic - hot and bothered