It was like the opening pages of a thriller. In the gathering dusk of an early winter evening last year, the postman handed me a package with a Belgian postmark and a cryptic symbol.

Inside, wrapped in layers of translucent paper, were two books, both in French. Nothing else. Needless to say, I was intrigued…
Dialectique du Monstre by Sylvain Piron revealed itself (with the use of Google Translate) to be a close study of the life and work of Opicinus de Canistris (1296-c.1353), a mysterious, psychologically tormented clerical official attached to the Avignon Papacy. The book is filled with reproductions of Opicinus’ elaborate parchment diagrams, which are like figments of the fever dreams of Archimedes or Leonardo; bizarre maps and masses of symbols harboring intimations just out of reach, a taproot into unseen connections between individuals, cities, whole worlds.
A while back, I wrote of the Electra Hypothesis, the idea that as the planet binds itself and its bit processes into an ever more interconnected web of radio links and optical fiber, its computational edges and nodes will develop into something of a sequel to Lovelock’s Gaia. Although layered in ambiguity, and separated by a gulf of time and mindset, Canistris seemed to have been drawn toward a similar notion.
The second book, opaquely titled 6/5, vaults the web of interconnection squarely into the modern world. Written by Alexandre Laumonier, the Sniper in Mahwah, it is a history of modern electronic markets and the rise of machines. In contrast to Dialectique du Monstre, it connects not to the past but to the future. The changes, computerization, machine learning, algorithms, that have swept over the financial markets are now spreading ever more thoroughly into an ever-wider range of endeavor.
The title 6/5 is a compressed code for a set of developments that have unfolded mostly out of view. The first part of the book, 6, refers to the floored number of milliseconds for a signal to travel from Chicago to New York on the fastest optical fiber. The second section, 5, alludes to the faster-than-glass signaling over the same route by microwave, which has now dropped two notches below that round number, to 3.982, within a sliver of the vacuum latency on the great circle connecting the endpoints.
A node of Electra’s graph. Hundreds of billions of dollars in coded trades rush daily through the towers of this Appalachian ridgeline.
For nearly a year, I’ve left a latin phrase at the top of the site… Pythagoreorum quaestionum gravitationalium de tribus corporibus nulla sit recurrens solutio, cuius rei demonstrationem mirabilem inveniri posset. Hanc blogis exiguitas non caperet.
The translation of the phrase is connected to the pythagorean three-body problem, another obliquely related topic involving descending integers that has seen regular rotation on oklo.org. A remarkable feature of Burrau’s original version of the problem (masses of 3, 4, and 5 started from rest under Newtonian gravity at the vertices opposite the sides of a 3-4-5 right triangle) is that the solution is almost, but not quite periodic. At time, T~15.830, bodies 4 and 5 almost collide, while body 3 nearly comes to rest. In a paper from 1967, Szebeheley and Peters show that a slight adjustment of the initial positions is sufficient to transform the situation into one that repeats itself endlessly.
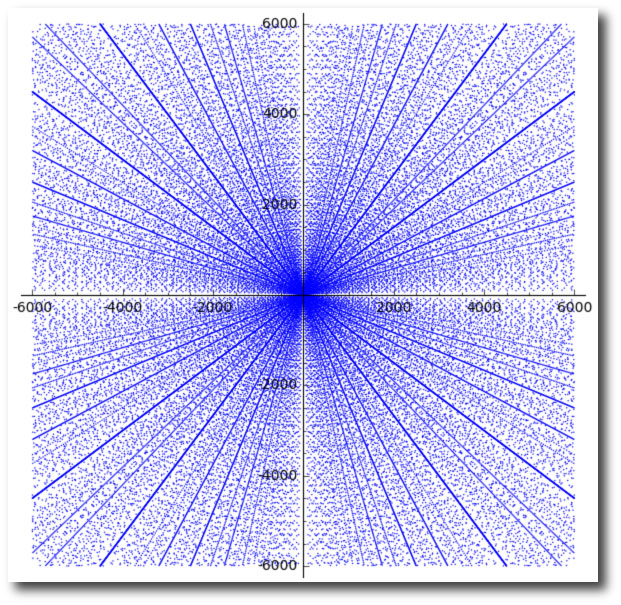
The integers 3, 4, and 5 are a single example drawn from the infinite set of Pythagorean triples, combinations of integers that correspond to the lengths of the the sides of right triangles. Each triple defines a variation on the original Pythagorean three-body problem, and I believe it’s the case that not a single member of this infinity of initial conditions will generate a periodic solution.
Scatter plot of the legs (a,b) of the first Pythagorean triples with a and b less than 6000. Negative values are included to illustrate the parabolic patterns. (Source: Wikipedia)
With a nod to Fermat, this assertion can be recast as a conjecture:
There exist no periodic solutions to any of the Pythagorean gravitational three-body problems. There may exist a truly marvelous demonstration of this proposition that this weblog has no space to contain.
Or at least it is true for every spot check that I’ve computed. For example, the tortured path of 20-21-29:

To place a tiny obstacle in the crush of progress, a translation into Latin beyond what Google can yet achieve seemed in order. I contacted Alexandre, who forwarded the request to Sylvain, who transmitted the following:
Pythagoreorum quaestionum gravitationalium de tribus corporibus nulla sit recurrens solutio, cuius rei demonstrationem mirabilem inveniri posset (could be found) /esse posset (could be). [Le verbe exstare (exister, être présent avec force) conviendrait mal àcette modalité.] Hanc blogis exiguitas non caperet.
Translation in English of “[Le verbe exstare (exister, être présentavec force) conviendrait mal à cette modalité]”: the verb “exist” would not be good here. inveniri posset seems to be the best solution.




Pingback: HFT in my backyard | S02E00 | Sniper In Mahwah