This Fall quarter, I taught a class for undergraduates on order-of-magnitude estimation in physics with a focus on astronomical examples. And on the last day of class, with final exams looming, what could be better that the time-tested stress relievers provided by the Fermi Paradox and the Drake Equation?
In Los Alamos National Laboratory publication LA-103110MS, “Where is Everybody?” An Account of Fermi’s Question, Eric Jones describes how Enrico Fermi, Emil Konopinski, Edward Teller, and Herbert York were diverted into their famous lunch-time conversation in the summer of 1950. While walking to the cafeteria, they were discussing news reports of UFOs, and an associated New Yorker cartoon that explained why the public trash cans in New York City were disappearing.
The flying saucers of the early 1950s hold a special fascination. A compound of Cold War anxieties — nuclear weapons, communists, infiltrators — they are silvery and remote, icons of minimalist design from a time when the space age was truly, rather than retro- futuristic.
Indeed, much of my own interest in astronomy can be traced to 50’s-era flying saucers. In the Bicentennial summer of 1976, after finishing third grade, I got a paper route delivering the Champaign-Urbana Courier. One of my customers, Mrs. Barbara Houseworth, had a garage full of cast-off books that she collected for an annual drive. I spent a great deal of time examining them whenever I visited to collect the subscription fee. I was particularly drawn to the pulpy paperback books — especially the ones with clay-coated photographic inserts — that covered the Bermuda Triangle, Bigfoot, the Loch Ness Monster, and Flying Saucers. All matters that seemed to merit the most urgent scientific concern.
At the top of my list was Gray Barker’s They Knew Too Much About Flying Saucers, published in 1956. I was so taken with it that Mrs. Houseworth simply gave me the book.
Gray Barker was an intriguing character, a closeted gay man in mid-century West Virginia who took a certain delight in channeling the fears and neuroses of the American masses into money-making volumes. Barker’s invention of the three men in dark suits, in particular, achieved a lasting cultural resonance. There is more about him at the UWV Center for Literary Computing, and he is the subject of several recent documentaries.
The message in the Cold War flying saucer books was crystal clear. Watch the Skies. And I did — on many clear dark Central Illinois nights with a Sears catalog 50mm refracting telescope…
Back to Friday’s class. We adopted the following form for the Fermi-Drake equation
$${N} = \Lambda ~f_{\star \rm{app}}~f_{\rm pl}~f_{\rm quqHP}~f_{\rm life}~f_{\rm macro}~f_{\rm intel}~f_{\rm tech}~L\,,$$
where \(N\) is the number of broadcasting civilizations in the galaxy, \(\Lambda\) is the number of stars formed per year in the Milky Way, \(f_{\star \rm{app}}\) is the fraction of stars with main sequence lifetimes long enough to support the development of a broadcasting civilization, \(~f_{\rm pl}\) is the fraction of stars with planets, \(~f_{\rm HP}\) is the average number of “habitable” planets per star, \(~f_{\rm life}\) is the fraction of these habitable planets that develop life, \(~f_{\rm macro}\) is the fraction of life-bearing planets that develop macroscopic life, \(~f_{\rm intel}\) is the fraction of macroscopic life-bearing planets that develop an “intelligent” life form (e.g. one that can orient itself abstractly in time), \(~f_{\rm tech}\) is the fraction of intelligent species that develop an understanding of the Maxwell Equations and build radios, and \(L\) is the civilization lifetime in years.
We defined and estimated two versions of \(L\). \(L_{\rm radio}\) is the average length of a time that a civilization leaks modulated electromagnetic signals into space. \(L_{\rm extinct}\) is the lifetime of the civilization, marked from the understanding of Maxwell’s equations to the point where the equations are collectively no longer understood.
The first few terms in the equation have been elevated from the realm of science fiction. I’ve adopted values of \(~\Lambda=10\,{\rm stars~yr^{-1}}\), \(~f_{\star \rm{app}}=0.75\), and \(~f_{\rm pl}=0.75\). Note that \(~\Lambda=10\,{\rm stars~yr^{-1}}\) is admittedly on the high side, even for 4.5 Gyr ago when star formation was somewhat more prevelant in the Galaxy.
Here is the table of values for the unknown terms, as estimated by the class members. I tried not to influence the results by telegraphing currently fashionable guesses. Twenty responses were collected:
| \(f_{\rm HP}\) | \(f_{\rm Life}\) | \(f_{\rm Macro}\) | \(f_{\rm Intel}\) | \(f_{\rm Tech}\) | \(L_{\rm Radio}\) | \(L_{\rm Extinct}\) |
|---|---|---|---|---|---|---|
| 0.10 | 0.01 | 0.3 | 0.1 | 0.2 | 1000 | 100000 |
| 0.10 | 0.70 | 0.01 | 0.6 | 0.001 | 500 | 10000 |
| 0.40 | 0.60 | 0.01 | 0.1 | 0.9 | 500 | 3000 |
| 0.20 | 0.90 | 0.08 | 0.4 | 0.002 | 500 | 500 |
| 0.01 | 0.90 | 0.05 | 0.001 | 0.2 | 1000 | 10000 |
| 0.01 | 0.1 | 0.1 | 0.01 | 0.001 | 1000 | 1000 |
| 0.10 | 0.01 | 0.1 | 0.1 | 0.01 | 100 | 1000 |
| 0.40 | 0.1 | 0.05 | 0.5 | 0.6 | 100000000 | 1000000 |
| 0.01 | 0.4 | 0.01 | 0.01 | 0.9 | 1000 | 10000 |
| 0.30 | 0.001 | 0.032 | 0.6 | 0.001 | 200 | 200 |
| 0.01 | 0.8 | 0.1 | 0.7 | 0.9 | 1000 | 1000 |
| 0.10 | 0.0001 | 0.01 | 0.001 | 0.02 | 500 | 150 |
| 0.10 | 0.2 | 0.1 | 0.01 | 0.1 | 10000 | 100000 |
| 0.10 | 0.9 | 0.25 | 0.01 | 0.5 | 10000 | 500000 |
| 0.30 | 0.001 | 0.01 | 0.6 | 0.9 | 500 | 3000 |
| 0.30 | 0.05 | 0.3 | 0.01 | 0.01 | 1000 | 1000 |
| 0.10 | 0.01 | 0.1 | 0.00001 | 0.00000001 | 300 | 5000 |
| 0.30 | 0.01 | 0.00001 | 0.01 | 0.0001 | 5000 | 5000 |
| 0.05 | 0.01 | 0.03 | 0.3 | 0.015 | 1000 | 150 |
| 0.02 | 0.01 | 0.1 | 0.01 | 0.001 | 100 | 100 |
With results:
Civilizations Currently Broadcasting in the Milky Way Galaxy
Average # 16,875
Median # 0.0016
Standard deviation 73,500
Max 337,500
Min 2.8125e-13
Civilizations Currently Present in the Milky Way Galaxy
Average # 185
Median # 0.013
Standard deviation 735
Max 3,375
Min 2.8125e-13
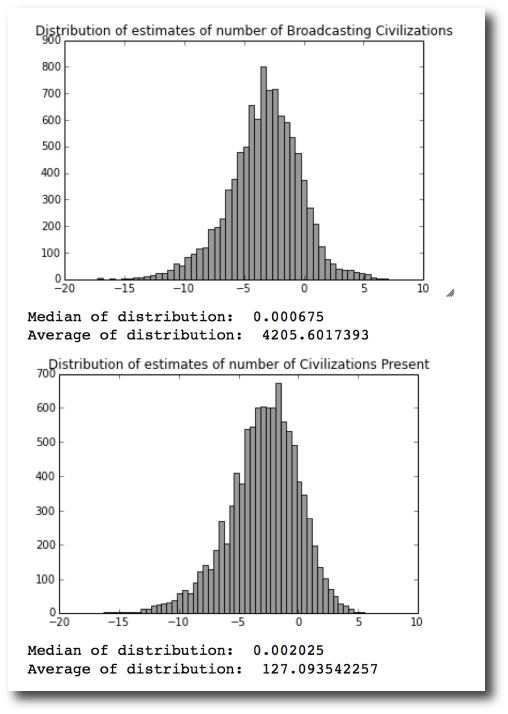
A smooth distribution of estimates for \(~{N}\) can be generated by drawing randomly from the list of estimates for each uncertain term in the equation, and then repeating for many estimates of \(~{N}\). Here are the histograms of estimates for the number of civilizations broadcasting from the galaxy and the number of civilizations present in the galaxy. The \(x\)-axes are \(\log_{10}N\).
The estimates point to the possibility that a civilization broadcasts for longer than intelligent members of the species exist. Two people implied this, by submitting values \(L_{\rm radio}>L_{\rm extinct}\). Looking at the table, there is one case where \(L_{\rm radio}\gg L_{\rm extinct} \gg \langle L \rangle\). The large values for \(L\) submitted by this person are causing the Average estimate for \(~{N}\) to substantially exceed the median estimate for \(~{N}\).
Adopting the \({ N=0.002}\) median of this distribution implies we need to look through \(\sim{n=500}\) galaxies to find the nearest broadcasting civilization, and that our nearest neighbors are \(\sim{ 8}\) Megaparsecs away. By the time one receives a message and replies to it, the intended recipient has long since gone extinct.