Image source: Drew Detweiler

The Pythagorean version of the gravitational three-body problem is very simple to state.

Assume that Newtonian Gravity is correct. Place three point bodies of masses 3, 4, and 5 at the vertices of a 3-4-5 right triangle, with each body at rest opposite the side of its respective length. What happens?

This particular problem seems to have been first posed in the late 1800s by the German mathematician Meissel, who mysteriously asserted that the motion of the three bodies should be periodic. That is, he felt that they would come back to their exact starting positions after executing a complex of intermediate motions. A first attempt at the solution — using numerical integration with a variable stepsize — was published in 1913 by Carl Burrau. He was able to map out the intial trajectories through several close encounters, but he was unable to integrate far enough to determine what eventually happens.

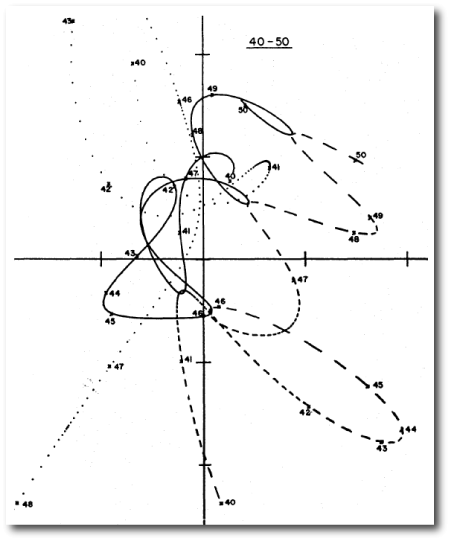
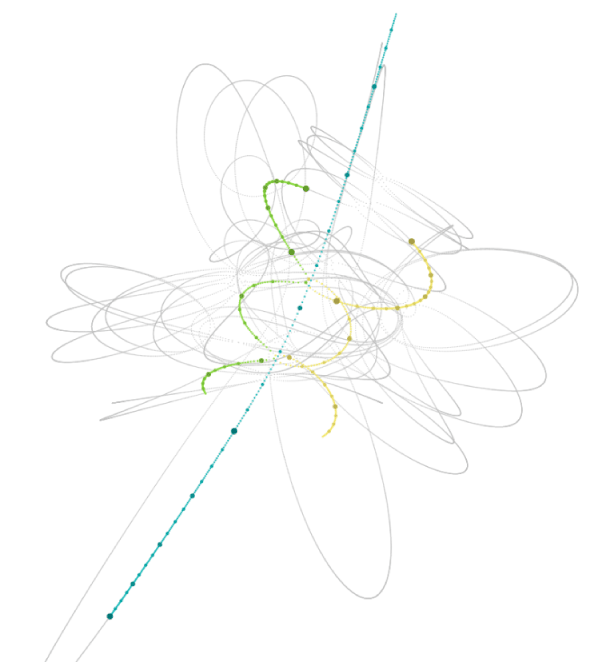
The correct solution was found in 1967 by Szebeley and Peters, who used the technique of three-body regularization to resolve the succession of close encounters. Here’s one of their diagrams showing a segment of the complicated motion.

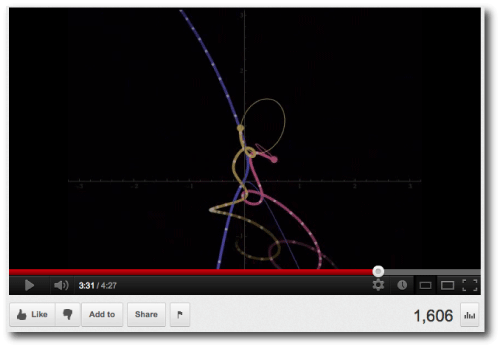
The Szebehely-Peters paper is fun to read. It emphasizes that this nonlinear problem is surprisingly tricky to solve, and that it shows the classic sensitive dependence on small variations in the initial conditions. For example, here’s a link to a recent, attractively rendered YouTube video that animates the trajectories and osculating orbits, as obtained via an implementation that uses Mathematica’s NDsolve.

Screenshot source.

Unfortunately, however, a careful analysis shows that the motion from 2:47 through the end of the video is completely incorrect…

I’ve always been struck by the fact that there’s a fascinating subtext to the trajectories of the three bodies if they are interpreted as a narrative of interpersonal relations. An initial value problem for a set of six coupled, first-order ordinary differential equations unfolds to telegraph a drama of attraction, betrayal, redemption, triumph and loss.

This summer, I had an opportunity to collaborate on the development of a scored, choreographed 3-minute 45-second performance of the problem which was premiered last month at the ZERO1 Biennial in San Jose. Our goal was to simultaneously convey the interpretive subtext while adhering to an fully accurate set of trajectories. It took a lot of work and was quite an intense experience. From the description at the ZERO1 site:

Three dancers in illuminated costumes create a live video visualization of the elliptic-hyperbolic solution to the classic Pythagorean three-body problem. A custom light tracing application detects light emitted from LEDs on the dancers’ soft circuitry costumes to create a visual model of their trajectories across the 2D plane of the stage. This realtime graphic visualization is projected on a large screen behind the stage in order to provide the audience with a birds eye perspective of their complex motion.

The use of digital technologies presents challenges for contemporary choreographic methods as data visualization guides movement through performative space on scientifically accurate trajectories. Live accompaniment from three musicians enhances physical performance as each body is interpreted through movement and sound. Feelings of longing, connection, and isolation are intertwined as the bodies are flung apart by the same gravitational forces that draw them together.

(That last sentence could more properly read, The bodies are flung apart despite feeling only attractive gravitational forces.)

To give a better sense, here are some notes and diagrams from mid-way through the process, as the choreography and the rehearsals were beginning to gel.

It’s particularly fascinating how the immediate outcome of the near-return to the pythagorean condition at the halfway mark is so different from how things unfold at the start of the piece. I like the interpretation that body 4 is somehow lazy at this point, or late to realize the import of the situation, and is marginalized as a result. This is the first real opportunity for bodies 3 and 4 to express emotion — shock for body 4, joy for body 3.

In the following measures, body 4 is marginalized, sulky, scheming, whereas body 3 is doing its best to impress, in the set of looping, private engagements. A reverie! The successive body 3-5 interchanges should _highlight_ the difference in masses between 3 and 5. Body 3 is light footed, fleet, body 5 glides smoothly, deliberately, (but not dully) as an anchor.

Body 4 must come back from its runout with a renewed sense of determination and purpose. The ensuing encounter between 4 and 5 must somehow convey 4’s charms and strengths. In a very real sense, this encounter is the tipping point that determines the outcome for all time. This is where the youtube video went off the rails.

As a consequence, there should be a sense of unfulfillment in the next body 3-5 encounter (a grasp, a gaze that fails to connect?) which sets up 3 to dive through on the way to its penultimate run-out. In this sequence, body 3 must somehow fail to live up to the expectations that it so brightly promised. The outcome is now determined, and the bodies know it, although the audience doesn’t.

While body 3 is at the arc of its final run-out, body 4 is weaving a spell on body 5, cementing the outcome ever more decisively. Indeed, Body 5 is only briefly engaged as 3 makes its final dramatic run through body 4 and 5’s orbit. The final sequence of encounters between body 4 should grow ever more identical, signaling the finality of the outcome.