It’s no exaggeration to assert that Galileo’s unveiling of Io, Europa, Ganymede and Callisto counts among the epic scientific discoveries of all time.

And certainly, it’s fair to say that the Galilean satellites of Jupiter constitute the original exoplanetary system. The Galilean satellites have been producing scientific insights for over four hundred years. Nearly all of the modern exoplanetary discoveries have antecedents — some quite recent, some centuries old — in Jupiter’s four moons.

The Galilean satellites can all be observed in transit across the face of Jupiter, and as early as 1656, the Sicilian astronomer Giovanni Hodierna, with his Medicaeorum Ephemerides, emphasized the importance of transit timing measurements for working out accurate predictive tables. In the late 1660’s, University of Bologna Professor Giovanni Cassini’s timing measurements and associated tables for the Jovian system were so impressive that he was tapped by Jean-Baptiste Colbert and Louis XIV to become director of the newly established Paris Observatory.

Giovanni Domenico Cassini (1625-1712). Prior to holding the directorship of the Paris Observatory, he was the highest paid astronomer at the University of Bologna, having been appointed to his professorship by the Pope.

Throughout the 1670s and 80s, Cassini wrestled with the fact that accurate transit timing measurements for the Jovian satellites create serious difficulties for models in which the moons travel on fixed orbits. Irregularities in the transit timings made from the Paris Observatory led to Ole Roemer’s determination of the finite speed of light in 1676, and by the early 1700s, observations of transit duration variations revealed that rapid nodal precession occurs in the Jovian system.

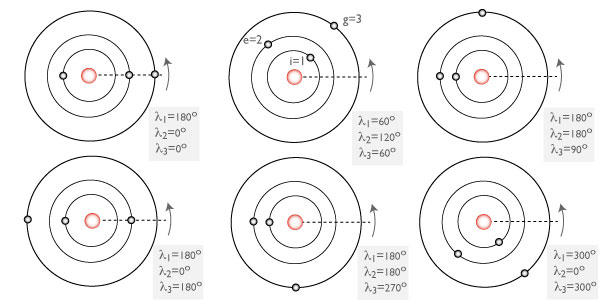
By middle of the Eighteenth Century, adequate data were in hand to demonstrate that a very curious relationship exists between the orbits of Io, Europa, and Ganymede. In 1743, the Swedish astronomer Pehr Wilhelm Wargentin (the first director of the Stockholm Observatory) published tables which made it clear that the 1:2:4 ratio in periods between Ganymede, Europa and Io is uncannily exact. Wargentin’s tables implied that a triple eclipse (in which all three satellites transit at once) would not occur until 1,319,643 CE at the earliest, and that the “argument”

between the mean longitudes of the satellite orbits is maintained to an extraordinary degree of accuracy. Geometrically, this means that the satellites engage in a cycle of six successive moon-moon conjunctions during the course of one Ganymedian orbit, and in so doing, manage to continually maintain ?_L=180°:

Laplace realized that a dynamical mechanism must be responsible for maintaining the cycle of conjunctions, and in 1784, was able to show that the angle ? is subject to a pendulum-like oscillation. If the satellites are perturbed slightly, then over the time, the satellite-satellite interactions conspire to cause ? to oscillate, or librate, back and forth about the equilibrium value of 180°. His theory for the satellites allowed him to derive the masses of the moons, and also predicted that the oscillation period for ? would be 2270d 18h.

In Laplace’s time, the observations were not accurate enough to sense any measurable amplitude for the libration — it appeared that the satellites were perfectly placed in the 1:2:4 resonant condition. We now know, however that ? librates with a tiny amplitude of 0.064°, and that the period of oscillation is 2071d, quite close to the value predicted by Laplace. Yoder and Peale (1981) have shown that the highly damped libration of ? can be understood as arising from a near-balance between tidal dissipation in Jupiter and tidal dissipation in Io. The presence of a dissipative mechanism has allowed the marble to have settled almost precisely into the bottom of the bowl.

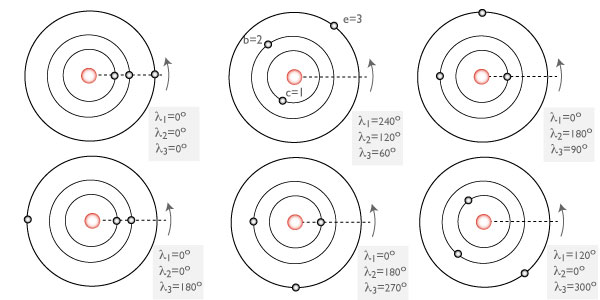
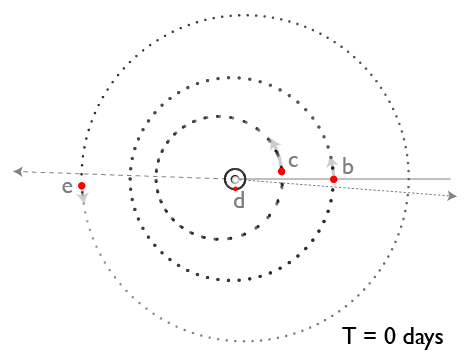
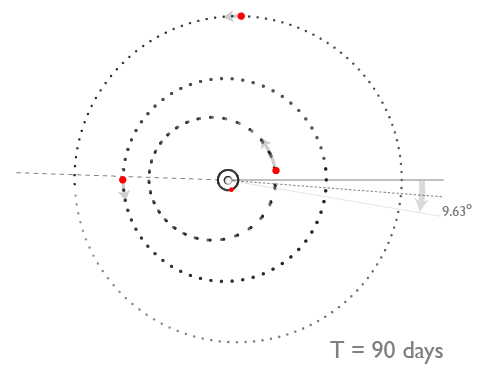
On this evening’s astro-ph mailing, our team has posted a paper that describes our discovery of a second example of a Laplace three-body resonance. Continued radial velocity monitoring of the nearby red dwarf star Gliese 876 has shown that the well-known P~30d and P~61d giant planets in the system are accompanied by an additional planet with a mass close to that of Uranus and an orbital period P~124d. In contrast to the Jovian system, the best fit to the observations shows that the Laplace relation is librating around ?=0°, and that triple conjunctions do occur. The diagram above is easily modified to convey the schematic geometry of the new system:

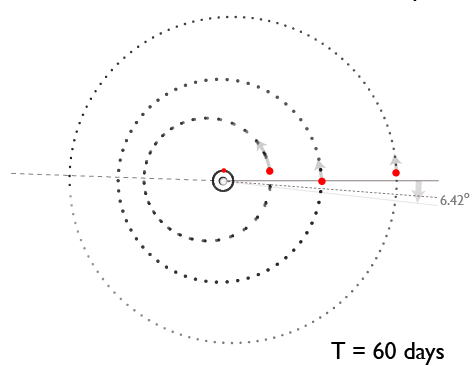
The actual state of affairs, however, is more complicated than shown in the above diagram. The total mass of planets in the Gliese 876 system is about 1% the mass of the central body, whereas Jupiter is roughly 5000 times more massive than its satellite system. This means that the Gliese 876 planets experience proportionally larger mutual gravitational interactions than do the Galilean satellites. In addition, the orbits are much more eccentric, and the planet-planet secular interaction causes a rapid precession of 14° per orbit of the outer planet. We can, however, plot the orbits in a co-precessing frame in order to view the cycle at four equal time intervals:

The libration of the Laplace argument, ?, around zero has an amplitude of ~40°, indicating that the GJ 876 “pendulum” packs a swing that’s 625 times larger than that of the Galilean satellites. Indeed, when the system configuration is integrated forward in time for hundreds of years, it’s clear that a simple pendulum equation is not able to describe the evolution of the Laplace angle. The oscillations are chaotic, with a Lyapunov time measured in a mere hundreds to thousands of years, and the theory, especially if there is a non-coplanar component to the motion, will require Laplace-level expertise in the use of the disturbing function…

There’s more… stay tuned for the next post.