It’s not often that a near-doubling of the planetary census arrives in one chunk, and so the paper detailing the latest Kepler results is of quite extraordinary interest.
It’s definitely going to be tricky to use the results in the Kepler paper to draw secure new conclusions about the true underlying distribution of planets. Nevertheless, the results look quite intriguing from the standpoint of back-of-the-envelope speculations.
Details: the paper contains a list of 312 candidate planets originating from 306 separate stars. A further 400 stars with candidate planets have been held back (see yesterday’s post), largely because they are either bright enough for high-quality Doppler follow-up at less-than-exorbitant cost, or harbor candidates with radii less than 1.5 that of Earth, or both. The paper states that the 312 candidate planets were primarily culled from an aggregate of 88,196 target stars dimmer than magnitude 14. The analysis is based on two blocks of photometry, one lasting 9.7 days (starting on May 2 2009) and one lasting 33.5 days (starting on May 13 2009).
The candidates have a slightly eclectic selection of associated data. The main table lists a radius, a transit epoch, and an orbital period for each candidate. There’s information about the parent stars as well, including apparent magnitude, effective temperate, surface gravity, and stellar radius. This is enough to make some intriguing plots. For example, the splash image for this post is a Hertzsprung-Russell diagram charting the locations of the candidates’ parent stars. The sizes of the points are directly proportional to the planet radii, and the color code is keyed to estimated planetary effective temperature. Most of the planets have surface temperatures of order 1000K or more, but there’s one rather singular object in the list, a 1.34 Rjup candidate on a 10389.109(!)-day orbit about a 9.058 solar radius G-type giant that (if it’s a planet) would have a photospheric temperature of order 180K. Certainly, a 1.34 Rjup radius is intriguing for such an object, as any non-pathological cold giant planet should be the size of Jupiter or smaller. Presumably, if the light curve showed evidence of a Saturn-style ring system, or better yet, an Earth-sized satellite, then KIC11465813 would chillin’ in the V.I.P. room.
A question of great interest is whether the list of candidates can add support to the recent radial velocity-based result that a large fraction of ordinary stars in the solar neighborhood are accompanied by a Neptune-or-lower mass planet with an orbital period of 50 days or less.
To get a first idea, I did the following quick (and extremely rough) Monte-Carlo calculation. I took 88,196 stars, and assumed that half of them have a planet with an orbital period drawn uniformly from the 1-d to 50-d orbital range. I then drew the planet masses uniformly from the 1-Earth-mass to 17-Earth-mass range, assumed Neptune-like densities of 1.6 gm/cc, circular orbits, and random orientations. For simplicity, the parent stars’ masses and radii are distributed uniformly from 0.7 to 1.3 times the solar value. I assumed that the 88,196 stars were observed continuously for 33.5 days, and require two transits to appear within the observation interval for a candidate to count. In keeping with the redaction policy, candidates are rejected if their radii were less than 1.5 that of Earth.
The simulation suggests that ~1100 candidate planets should be present in a 88,196 star sample. Encouragingly, this is at least order-of-magnitude agreement, although there’s a hint that the Kepler yield might be lower than what the RV results are implying. It will be very interesting to see what a more careful comparison has to say…

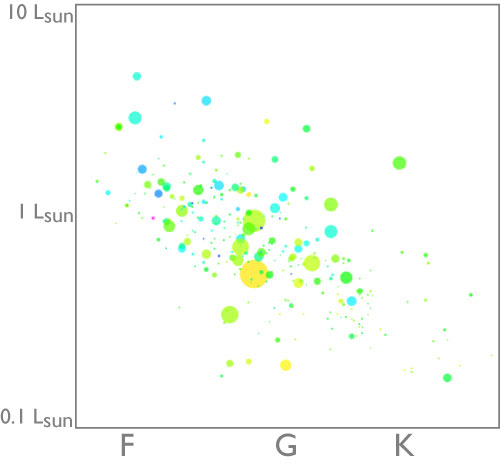
Surely the 10,000+ d period planet is a typo in the chart. They state that all candidates had multiple transit observations.
I think it might be right — I think it says somewhere in the paper that some of the appendix candidates are based on a single transit. (The paper is a little obscure in places).
I dunno, the paper also states that the list includes objects which have only a single transit for purposes of completeness (page 5). Unless of course all periods over about 15 days or so are typos? I guess a 28 year period means no-one’s going to be able to claim a solid characterisation for a while…
If indeed it is not a typo, how would they determine the period of the planet with only a single transit?
Good question Hungry…
I guess you have to make the assumption the orbit is circular and use the transit duration to estimate the orbital period. Not sure how you’d handle the effect of inclination on the duration, perhaps the shape of the transit combined with limb darkening models, or maybe just take i=90 degrees?
Was giving it a little more thought.
A ~28 year period around a giant star is going to produce a very long transit duration. A sampling rate of twice per hour (as is given in the paper) may be enough to determine the impact parameter via the ingress/egress shape, allowing the linear velocity across the stellar disk to be known with unusually high accuracy.
Then it’s trivial to solve for an orbital period.
@nhermis
To determine the period with only a single transit observed, they must have used the transit duration. They mention using that info on p.4-5 in item 1 to check for consistency. For single-transit events, they must have assumed a stellar mass and radius based on the Kepler input catalog info and calculated a predicted period based on transit duration. Must have also assumed an equatorial transit.
Just my 2 cents. It makes sense if they’re just trying to get a quick & dirty estimate.
Again, may not be necessary to assume any value of b if the ingress and egress was sufficiently long to measure with a 30 minute cadence.
@ drpepper
As I eluded to in the post just above yours, if the transit lasts a very long time, the sampling rate may be high enough to constrain the impact parameter, and there will be no need to assume an equatorial transit.
Sorry for the double post, It didn’t seem to post it the first time.
Even if you know b, don’t you still need an independent eccentricity constraint to get a period?
Indeed. You’d have to assume some value for the eccentricity for that to work.
Kepler will probably not observe this planet in transit again. RV monitoring may be the best way to constrain its orbital period.
@cwmagee
Technically yes, but as long as the eccentricity is not too high AND the transit is not near perihelion or aphelion, your period estimate will still be pretty good.
@Hungry4info2
Speed of the transit could tell you.
@ atomic7732
Transit duration is not only a function of the orbital velocity, but of the impact parameter. Without knowing the impact parameter, the transit duration of a long period planet with grazing transit is matched by the transit duration of a short period equatorial transiting planet.
Pingback: Populär Astronomi - » Meningsfulla blinkningar från andra solsystem