
In a nutshell, here’s the question: “What are the odds that the planets will experience a dramatic orbital instability before the Sun turns into a red giant and destroys the Earth?”
In a nutshell, here’s the answer: “About 1%.”
I’m very happy that it’s now possible to write a full follow-up report on last summer’s post about UCSC physics undergraduate Konstantin Batygin’s work on the long-term stability of the solar system.
Recapping last summer’s post:
The long-term stability of the planetary orbits has been a marquee-level question in astronomy for more than three centuries. Newton saw the ordered structure of the solar system as proof positive of a benign deity. In the late 1700s, the apparent clockwork regularity of interaction between Jupiter and Saturn helped to establish the long-standing concept of Laplacian determinism. In the late Nineteenth Century, Poincaré’s work on orbital dynamics provided the first major results in the study of chaotic systems and nonlinear dynamics, and began the tilt of the scientific worldview away from determinism and toward a probabalistic interpretation.
In recent years, it’s become fairly clear that the Solar System is dynamically unstable in the sense that if one waits long enough (and ignores drastic overall changes such as those wrought by the Sun’s evolution or by brushes with passing stars) the planets will eventually find themselves on crossing orbits, leading to close encounters, ejections and collisions.
Desktop PCs are now fast enough to integrate the eight planets into the future for time scales that exceed the Sun’s hydrogen burning lifetime. This makes it possible to explore future dynamical trajectories for the solar system. Over the long term, of course, the planetary orbits are chaotic, and so for durations longer than ~50 million years into the future, it becomes impossible to make a deterministic prediction for exactly where the planets will be. The butterfly effect implies that we can have no idea whether January 1, 100,000,000 AD will occur in the winter or in the summer. We can’t even say with complete certainty that Earth will be orbiting the Sun at all on that date.
We can, however, carry out numerical integrations of the planetary motions. If the integration is done to sufficient numerical accuracy, and starts with the current orbital configuration of the planets, then we have a possible future trajectory for the solar system. An ensemble of integrations, in which each instance is carried out with an unobservably tiny perturbation to the initial conditions, can give a statistical indication of the distribution of possible long-term outcomes.
Here’s a time series showing the variation in Earth’s eccentricity during a 20 billion year integration that Konstantin carried out. In this simulation, the Earth experiences a seemingly endless series of secular variations between e=0 and e=0.07 (with a very slight change in behavior at a time about 10 billion years from now). The boring, mildly chaotic variations in Earth’s orbit are mostly dictated by interactions with Venus:

Mercury, on the other hand, is quite a bit more high-strung:
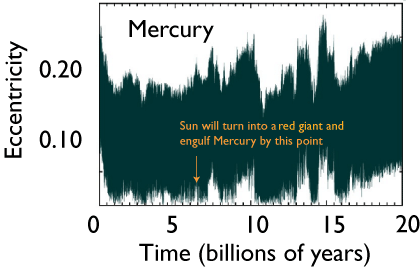
These two plots suggest that the Solar System is “good to go” for the foreseeable future. Indeed, an analysis (published in Science in 1999) by Norm Murray and Matt Holman suggests that the four outer planets have a dynamical lifetime of order one hundred quadrillion years (ignoring, of course, effects of passing stars and the Sun’s evolution).
Work by Jacques Laskar, on the other hand, who is Laplace’s dynamical heir at the Bureau des Longitudes in Paris, suggests that the inner solar system might be on far less stable footing.
Laskar performed the following experiment (described in this 1996 paper, which is well worth reading). Using an extremely fast (but approximate) numerical code which incorporates more than 50,000 secular perturbation terms involving the eight planets, Laskar integrated the current configuration of the Solar System 2 billion years into negative time. He then made four “realizations” of the solar system in which Earth’s position was shifted by a mere 150 meters in different directions. These four nearly identical variations of the Solar System were each integrated backward in time for a further 500 million years. Due to the highly chaotic nature of the system, each of Laskar’s four simulations spent most of the computational time exploring entirely different dynamical paths within the Solar System’s allowed phase space.
When the four integrations were complete, Laskar examined the individual orbital histories and selected the trajectory in which Mercury’s eccentricity achieved its largest value. The Solar system configuration at the time of this greatest eccentricity excursion was then used as a starting condition for a second set of four individual 500-million year integrations. At the end of this second round of calculations a new set of starting conditions was determined by again selecting the configuration at which Mercury’s excursion was the largest.
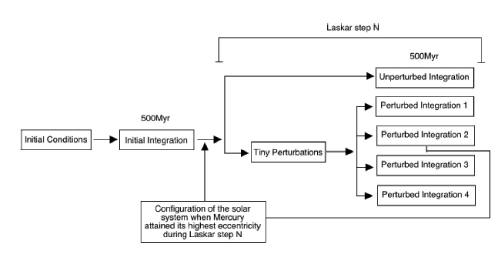
Here’s a diagram that flowcharts (using positive time) the basic idea underlying Laskar’s bifurcation method:
After 18 rounds, which when pieced together yielded a 6 billion year integration, Laskar observed that Mercury’s eccentricity had increased to e>0.5. Mercury, and indeed the entire inner solar system, had gotten itself into extremely serious trouble. A secular integration scheme can’t handle close encounters, though, and so the final gory details were left to the imagination. Nevertheless, it was clear that by the end of Laskar’s simulation, Mercury was in line to suffer a close encounter with Venus, or a collision with the Sun, or an ejection from the Solar System. The 1996 Laskar integration was the first explicit demonstration of the Solar System’s long-term dynamical instability. In essence, it brought a 300-year quest to a dramatic head.
I read Laskar’s paper in 1999, shortly after the discovery of the Upsilon Andromedae planetary system spurred me into a crash-course study of orbital dynamics. His calculations seemed to raise some really interesting questions. What is the dynamical mechanism that destabilized the inner Solar System? Was the elevation of Mercury’s eccentricity a consequence of the secular perturbation approach that he applied? Would his bifurcation strategy find a similar result when used with direct numerical integration of the equations of motion?
Two years ago, I told Konstantin about Laskar’s experiment, and we decided to see if we could answer the questions that it raised. As a first step, Konstantin set about replicating Laskar’s simulation strategy with full numerical integrations. All told, this required over a year of computing, including a lot of effort to make sure that the buildup of numerical error was kept under control.
Our version of Laskar’s method works as follows (and is shown in the flow chart above). First, a direct integration spanning 500 million years, ~100 Earth Lyapunov times, is made using the current Solar System configuration as a starting point. Picking up at the integration’s endpoint, five solutions for 500 million years are computed. Four of these use initial conditions in which Earth’s position is shifted, while one uses the unaltered solution. Because initial uncertainties diverge exponentially with time, a shift of 150 meters in Earth’s position 500 million years from now corresponds to an initial error today of order 10^-42 meters — ten orders of magnitude smaller than the Planck scale. After the five bifurcated trajectories are computed, the solution in which Mercury attains the its highest eccentricity is preserved to the nearest whole million years, and five new trajectories are started.
Much to our amazement, the bifurcation strategy is capable of showing Mercury the door in a hurry. In our first complete experiment, only three Laskar steps were required in order to coax Mercury into a collision with Venus at a time 861.455 million years from now:
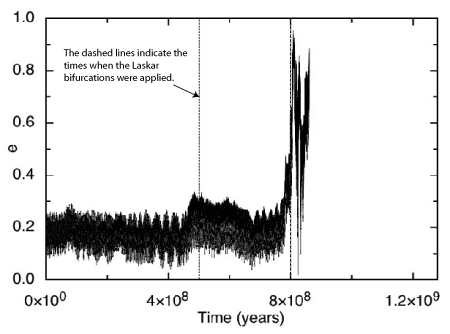
And it wasn’t only Mercury that ran into problems. At t=822 million years, shortly after Mercury’s entrance into a zone of severe chaos, Mars — rovers and all — was summarily ejected from the Solar System:
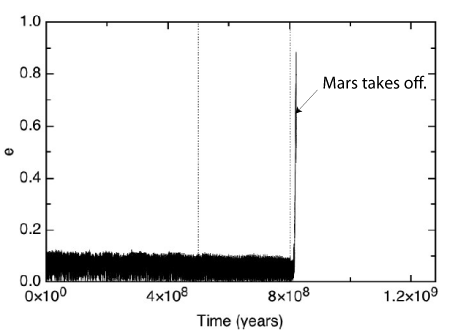
This is some pretty heavy stuff. We have a direct numerical solution of Newton’s equations in which the solar system goes unstable well before life on Earth is expected to perish. (Can GR save the day? Read the paper.)
So what’s the mechanism that causes the instability?
At first, we thought that the dynamics were stemming from an overlap of mean motion resonances, but we were able to show that isn’t the case. In the end, Konstantin used the technique of synthetic secular perturbation theory to demonstrate that the culprit is a linear secular resonance with Jupiter. In short, Mercury winds up in a situation where the resonant argument (omega_1 – omega_5) librates between +19.8 and -43.56 degrees for three million years. The result is a steady increase in Mercury’s eccentricity to a dangerously high value:
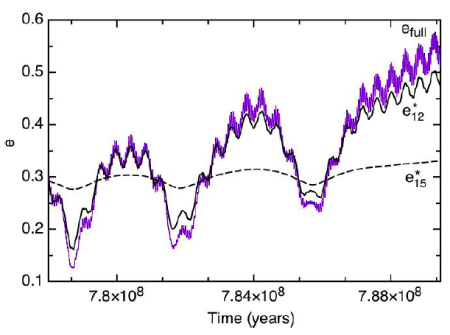
The evolution of Mercury’s orbit is driven both directly by Jupiter, and to a greater extent by Jupiter’s influence transmitted through Venus. It’s an amazing, scary possibility, and the full details are in the paper.
Needless to say, we were thrilled when the full picture came together. We wrote up our work and submitted it to the Astrophysical Journal in mid-January. I got in touch with the UCSC public affairs office with an eye toward issuing a press release once our paper cleared the refereeing process.
Then, to our total astonishment and dismay, we were scooped! It turns out that Jacques Laskar himself has also been working on the problem. On February 22nd, he posted an astro-ph preprint of a paper that will be appearing in Icarus. He beat us to the punch with a basic result that’s fully in line with what we found. Here’s his astro-ph abstract:
A statistical analysis is performed over more than 1001 different integrations of the secular equations of the Solar system over 5 Gyr. With this secular system, the probability of the eccentricity of Mercury to reach 0.6 in 5 Gyr is about 1 to 2 %. In order to compare with (Ito and Tanikawa, 2002), we have performed the same analysis without general relativity, and obtained even more orbits of large eccentricity for Mercury. We have performed as well a direct integration of the planetary orbits, without averaging, for a dynamical model that do not include the Moon or general relativity with 10 very close initial conditions over 3 Gyr. The statistics obtained with this reduced set are comparable to the statistics of the secular equations, and in particular we obtain two trajectories for which the eccentricity of Mercury increases beyond 0.8 in less than 1.3 Gyr and 2.8 Gyr respectively. These strong instabilities in the orbital motion of Mecury results from secular resonance beween the perihelion of Jupiter and Mercury that are facilitated by the absence of general relativity. The statistical analysis of the 1001 orbits of the secular equations also provides probability density functions (PDF) for the eccentricity and inclination of the terrestrial planets.
Rather ironically, Laskar did not use his bifurcation method to solve the problem. By sticking with his secular code, he’s able to get a big speedup over direct numerical integration, which allowed him to perform a suite of 1001 straight-line integrations of the secular equations. The resulting statistics of these allow him to place a 1-2% probability of Mercury going haywire within 5 billion years. (With general relativity included, this number is probably closer to 1%, although his integrations in the GR case haven’t finished yet.)
So sadly, no UCSC press release will be forthcoming. Priority of discovery goes to the Bureau of Longitudes, and our paper, which will be appearing in the Astrophysical Journal, will be providing dramatic confirmation of the mechanism by which the Solar System can come undone.
Our paper (Batygin, K. & Laughlin, G. 2008, Astrophysical Journal, In Press.) is available on astro-ph.

Very interesting. Is the instability inherent in the orbits of the planets, or is it that we cannot predict what future physical changes to the planets will do their orbits in the long run (e.g. redistribution of mass due to plate tectonics, or large asteroid collisions, etc)?
And what would be the first sign that a “haywire” event was about to happen? How much warning would there be of such an event–are we talking millions of years or just a few hundred?
Sounds like a fascinating subject for a science fiction novel!
Hi Tactius,
the instability observed here is entirely inherent to the orbits. The unstable solutions are simply possible scenarios for the Solar System’s future. In fact, there were no asteroids present in our numerical model, and all bodies were treated as point-masses.
The mechanism which drives Mercury’s eccentricity to high values is linear secular resonance, so one would look to the frequency of the difference of perihelion precession rates of Mercury and Jupiter for a warning. If this frequency goes to zero, we’re in trouble. However, a secular cycle takes place over million year time-scales, so we would have a pretty early warning. For instance, right now, d(Omega1-Omega5)/dt ~ 1arcsec/yr = 1 cycle/1.3Myr.
This would be a pretty cool novel indeed! :)
If I understand the paper correctly, you aren’t including tidal forces in the integration. Would the effect of tides to circularise the orbit disrupt the resonance?
Hi Andy,
tidal dissipation would no doubt attempt to save the day. Both, the circulization of the orbit and the decrease of semi-major axis would affect Mercury’s precession rate, but of course the actual damage depends significantly on the Q. My instinct is that tidal dissipation is too slow in competition with linear secular resonance, and Mercury would have the chance of attaining e > 0.7 before the tidal forces would significantly alter the g1 eigenfrequency.
Incredibly beautiful work.
Two naive questions from someone who works in an entirely different domain (protein folding):
Could it be possible to generalize the results and obtain a back-of-the-envelope estimate of the number of rogue planets in the Galaxy, for example?
Moreover: if the chances of such planets to cross our planetary system are probably small or negligible (given the little cross-section), maybe the odds of them perturbing comets or other objects in the Oort cloud are significant. Again, what could be those odds? Could these rogue planets have a significant role in the evolution of solar systems?
Hi Devicerandom,
Interesting idea – I think in order to get a rough estimate of the number of rogue planets, it would pay to study the dynamics of the earlier stages of planetary systems’ evolution in general, since the dynamics are more violent. Given that the process of planetary formation can be well modeled, with a large amount of computer power, one could get a probabilistic estimate.
I believe that the perturbative effect of rogue planets to the Solar System is rather negligible, and is probably lost in the soup of extrasolar perturbations. Nevertheless, I think rogue planets are pretty cool.
I can’t but agree that rogue planets are cool objects, so I can’t but think about them now…
I think in order to get a rough estimate of the number of rogue planets, it would pay to study the dynamics of the earlier stages of planetary systems’ evolution in general, since the dynamics are more violent.
Right, wasn’t thinking of that.
Sorry if I insist, but… In your opinion, what order of magnitude can we expect for the average number of planets that are ejected from a star system?
Let me spam a bit my estimates… Your 1% estimate for the ejection of the inner planets of the solar system in its lifetime is pretty high. If, even taking into account early stages of planet formation the average is much less (say 0.1-0.001%), it means that in the Galaxy there is something like 10^7-10^8 planetary bodies not bound to any particular star. Which sounds impressive, but is a pretty small number, because there could be much less of these objects than stars – our chances to encountering one close in our solar system are far less than meeting an actual star. However they would be not exactly rare. Is there any chance to detect such objects? They look incredibly tricky to find to me (much more than bound exoplanets), but…
Much more titillating would be to find that a substantial percentage of stars, in their early formation, eject planetary bodies. What you say -and the little I know- about the “violence” of early planet formation seems to point towards that. This would mean that the Galaxy is teeming with such objects -say, 10-100 billion rogue planets. Seems fascinating.
I am also thinking that such objects would tend to accumulate, since they are basically cold objects that do not undergo a significant evolution.
Sorry for my trivial late-night babble…
Hmmm… if we assume that the dynamical structure of our Solar System is at least somewhat representative of other systems, in a planetary system’s total lifetime, I would expect an average of ~ 6±5.5% of its planets to escape. Then again, my guess could be completely off (It has happened before :).
It is indeed intriguing to think about the fate of these objects, once they have escaped. Dave Stevenson (Nature, 1998) wrote a paper about the possibility of life being sustained on interstellar planets due to geothermal processes.
As far as detection goes, I have no idea ultra-precise gravitational lensing perhaps?
Have you guys looked at the periodicity of eccentricity changes?
This might be worthwhile if you wish to continue this research. The reason is that the periodicity of the Earth’s change in orbital parameters are recorded geologically. Milankovitch cycles are climactic cycles caused by the Earth’s axial tilt, precession, and eccentricity. They have been investigated at least as far back as 2e8 years, so if you want to “ground-truth” your models of eccentricity evolution, this would be one way to do so.
If you’re interested, a place to start is:
Olsen, P.E., and Whiteside, J.H., 2007, Pre-Quaternary Milankovitch cycles and climate variability, in Gonitz, V. (ed.), Encyclopedia of Paleoclimatology and Ancient Environments, Earth Science Series, Kluwer Academic Publishers, Dordrecht, the Netherlands (in press).
Of course, since precession and axial tilt are dominated by lunar effects, you’d need to include a moon in future runs to compare them…
Pingback: ¿Es estable el Sistema Solar? (o Mercurio y Venus colisionarán, y Marte abandonará el Sistema Solar, según simulaciones numéricas) « Francis (th)E mule Science’s News