Janus and Epimetheus Source: JPL

Last week, I wrote a post about the negative heat capacity of self-gravitating systems. I never cease to find it remarkable that if you drain energy out of a system that is held together by its own gravity (such as a giant planet, or a cluster of stars), then that system gets hotter. There really is such a thing as a free lunch, brought to you courtesy of the attractive gravitational force.

A collection of bodies orbiting a larger body is a self-gravitating system, and therefore will also display a negative heat capacity. We illustrated this with the idea of a satellite running through a cloud of dust. Friction between the satellite and the dust heats both bodies up, and they radiate energy away to space. The satellite simultaneously spirals into an orbit with higher velocity, and hence a higher kinetic energy, or temperature.

A family of orbital trajectories known as horseshoe orbits present a riff on this basic principle. A horseshoe orbit occurs when two bodies, with slightly different orbital periods, start off in near-circular orbits on opposite sides of a large central mass. The body with the shorter orbital period eventually attempts to overtake the body with the longer orbital period.

As the short-period body catches up with the long-period body, an attractive gravitational force is exerted between the pair. This force pulls the short-period body forward, and pulls the long-period body back. That is, the gravitational interaction leads to an exchange which drains orbital energy from the long-period (leading) body, and gives energy to the short-period (trailing) body. This exchange causes the bodies to swap orbital periods. The long-period body gets a shorter period, and the short-period body gets a longer period. In a frame that rotates with the average orbital velocity of the pair, the two bodies eventually come in to contact again on the opposite side of the star, and the process is repeated. Again and again in an mindlessly delicate cycle.

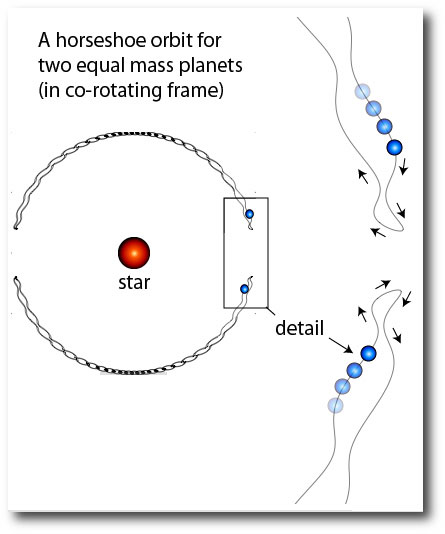
The orbital trajectory in the above figure is lifted and adapted from a paper in the Astronomical Journal that I wrote with John Chambers. In that paper, we studied a number of weird co-orbital planetary configurations, and speculated that they might eventually be observed using the radial velocity method. If you can’t fit a particular data set with the console, the horseshoe configuration is always a good thing to check.

In our own solar system, there are two small Saturnian moons, Janus and Epimetheus, which are caught in a horseshoe-like orbit. The splash picture for today’s post shows a Cassini photograph of these moons taken near the time during which they exchange periods.

One of the most useful features of systemic console is its ability to sonify radial velocity waveforms. The soundfiles are produced by making a full integration of the equations of motion, hence all of the nonlinear gravitational interactions between the bodies are incorporated into the sound. When the console is used as a nonlinear digital synthesizer, the horseshoe orbits provide a method for producing amplitude modulation of a tone. To see how this works, launch the downloadable console, and set up the following system (just ignore the radial velocity data, since we’re not interested in fitting, but rather just in waveform generation):

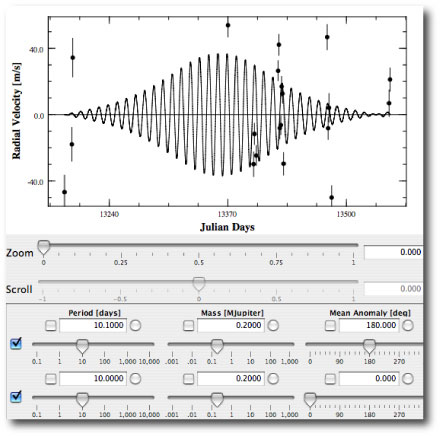
That is, set up two 0.2 Jupiter mass planets with mean anomalies of 0 and 180 degrees. Make the period of one planet 10.1 days, and the other 10.0 days. For simplicity, keep the eccentricities at zero. Clicking the integration box shows the resulting radial velocity waveform. When the planets are on opposite sides of the star, their radial velocity influences on the star cancel. When they are on the same side of the star, their radial velocity influences are additive. This gives an overall modulation envelope on top of the fundamental ~10.05 day period. Use the sonify button to create a 220 hz tone out of this system:

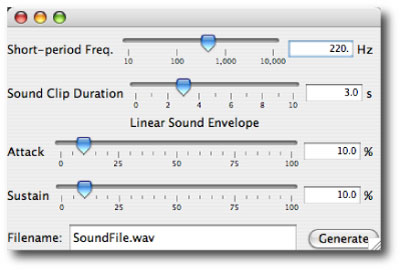
Here’s a link to the resulting .wav file. The amplitude modulation (or tremolo) can clearly be heard.

Try building some more complex sounds by nesting horseshoe orbits, and using unequal masses. If you get something cool, e-mail me at laughlin ucolick edu.