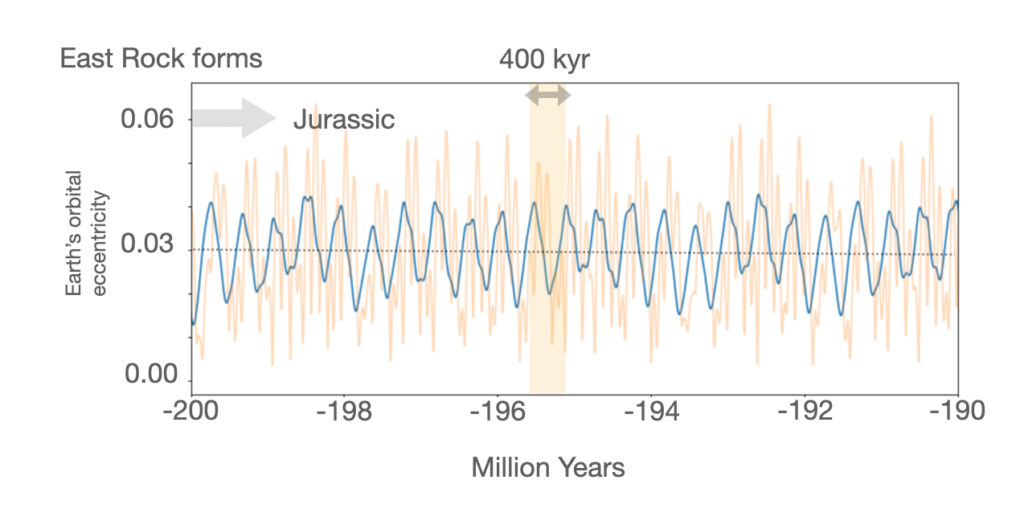
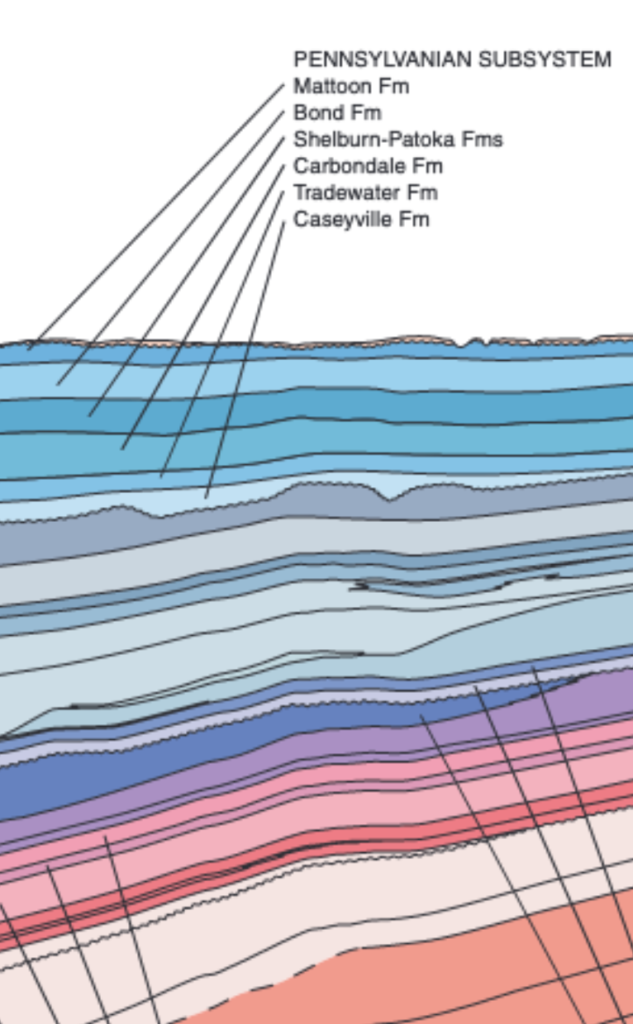
Geologically speaking, not much has happened in Illinois since the Permian. In particular, in the ultra-flat vicinity of Urbana where I grew up, there is no exposed bedrock at all. If one takes the effort to dig down through meters of topsoil and glacial till, one eventually hits gray, unmetamorphosed 320-million year old sediments from the Carboniferous — the Mattoon Formation — the crumbly picture of a disappointing drill core.

Something about those miles of dull strata directly underfoot instills a vicarious appeal into the IGS maps for the entire state. And while they are dominated by the vast bland extent of the coal-rich Illinois basin, the margins of the map hint at strange and exotic features, including one, Hicks Dome, that’s so weird that it merits its own circular inset.

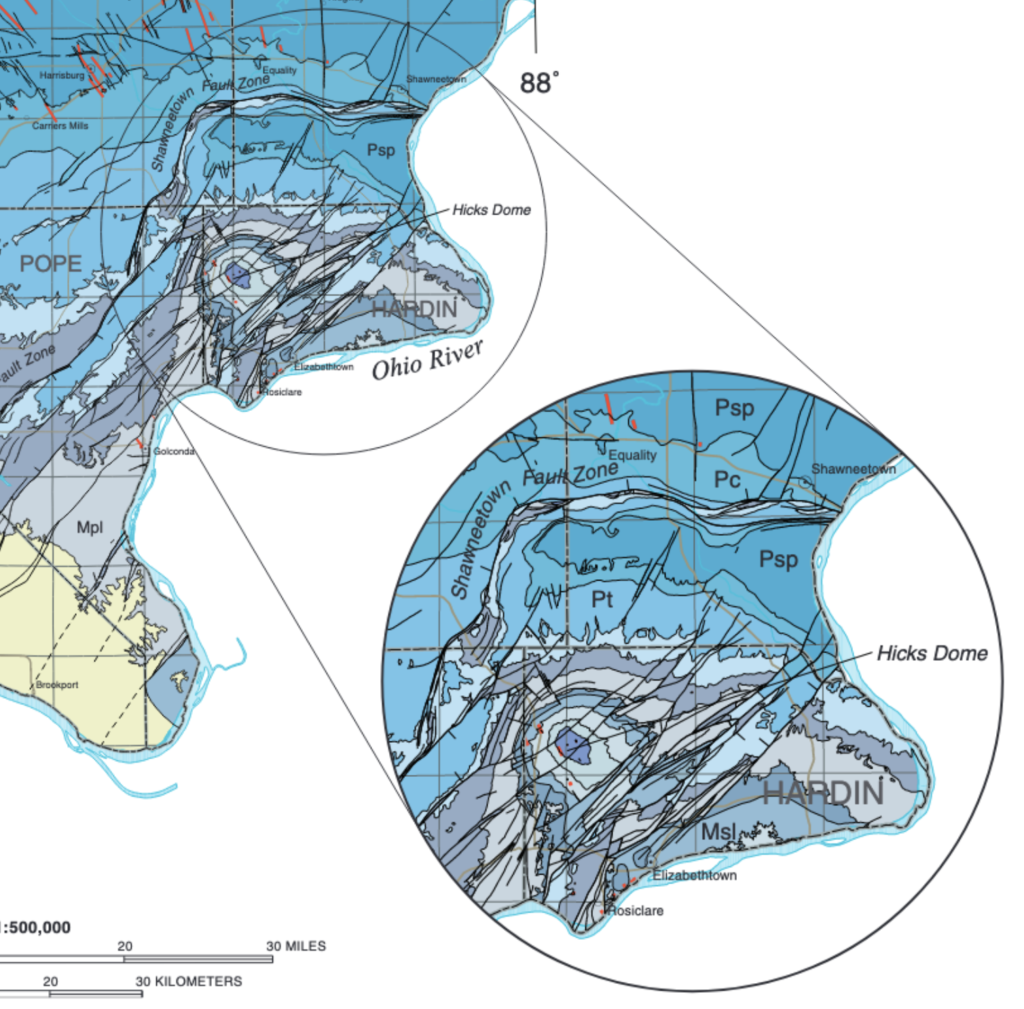
The southeastern tip of Illinois is riddled with faults, and pocked by a mysterious, crater-like 275-million year old blemish that is still clearly visible in aerial photographs. The strata that comprise this feature — the Hicks Dome — were pushed up thousands of feet by a carbon dioxide-driven explosion that brecciated the rock miles below and squeezed dikes of lava through cracks toward the surface.

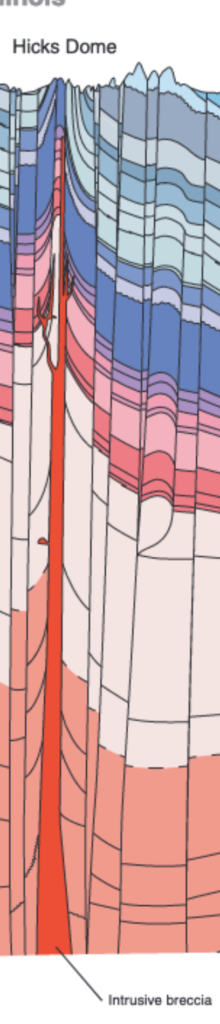
The resulting igneous rocks, which are colored red in the diagram just above, can be extracted from drill cores. Mineralogical tests indicate that the lava ascended at least 25 km from a source of origin in the upper mantle. Then later, during the Jurassic, geothermally heated brines seeped through the faults that shattered the sediments and interacted with limestone to form fabulous fluorite crystals.

An even more remarkable example of a deep-Earth intrusion is located in Arkansas, 383 miles southwest of Hicks Dome. The Prairie Creek Diatreme, more evocatively known as the Crater of Diamonds, is a 106-Myr old igneous pipe filled with solidified lamproite lava that was driven upward (as also occurred at Hicks Dome) by exsolving CO2 gas from a source at least 100 miles down. The crater, moreover, is indifferently salted with actual diamonds, including the occasional big-deal gem.

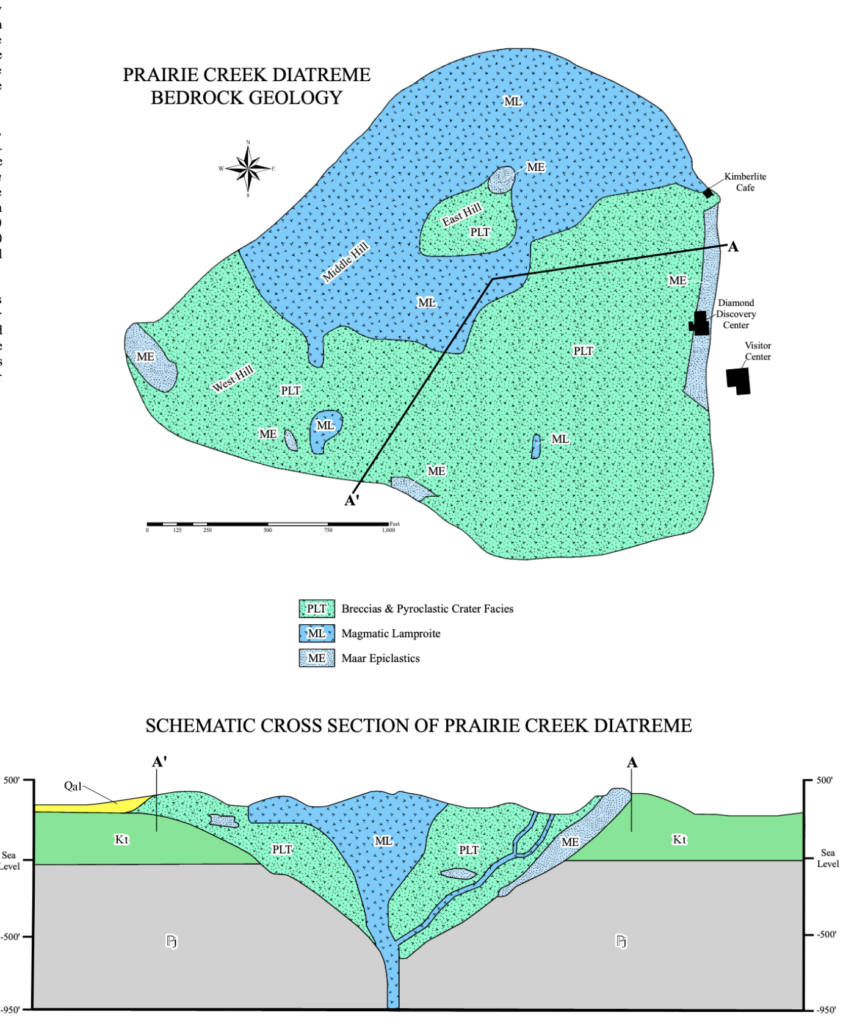
Diamonds are metastable when removed from deep mantle conditions, and so in order for them to survive a lava-soaked mix-mastered trip to Earth’s surface, the transport has to be rapid. The lamproite that brought up the diamonds must have smashed its way through a hundred miles of rock with a vertical velocity of order a hundred miles per hour, a marshaling of forces that is undeniably impressive, and indeed, at first glance, completely non-intuitive.

Satisfyingly, a hundred and six million years after the cryptoexplosion, Arkansas is running the lamproite pipe as a State Park, offering end-runs around de Beers at very reasonable rates:

Earth’s last diamond-bearing eruptions occurred tens of millions of years ago. It’s a good thing they aren’t every-day occurrences. Methane gas, however, is currently causing new-school cryptoexplosions that leave ominous lake-filled craters in the permafrost of the Siberian tundra.

On Earth, the crypto prefix can generally be detached from cryptoexplosions once the techniques of laboratory and field geology have been brought to bear. Kimberlite eruptions may seem superficially crazy, but the basic mechanism of their operation is increasingly well understood. Truly mysterious explosions need to occur off Earth, in locations where it’s not yet possible to go in and root around after the fact…

All the small things. Truth cares truth brings. I’ll take one lift. Your ride best trip… Vintage Blink played in the background. Tubular radio bulbs placed a diffuse glow on the distressed wood and polished concrete surfaces. The researcher pushed away a half-finished bowl of microgreens and, before taking another sip of single-origin espresso, eyed me with a look somewhere between amusement and concern.

“I mean really. You sound like a relic. You’ve gotta move on. You’ve gotta get with the times. ‘Oumuamua is so 2020. Everyone who’s anyone now is working on UAPs.”

It’s true that the cutting-edge has progressed to bigger and weirder things. Indeed, it’s now been over four years since ‘Oumuamua raced out of sight, and I can’t seem to let that mysterious cosmic visitor out of mind.

The ISO story has been worn smooth through years of retelling, and the details are probably well known to anyone who reads oklo.org: ‘Oumuamua entered the Solar System on a strongly hyperbolic trajectory consistent with a pre-encounter galactocentric obit that was quite close to the local standard of rest. It closed to within 0.25 AU of the Sun. Then, just after passing Earth’s orbit on its outbound leg, it was detected by Pan-STARRs at the end of the third week of October, 2017. Global follow-up efforts with space and ground-based telescopes were quickly mounted. ‘Oumuamua was observed to have a strongly varying light curve, no detectable coma, a slightly reddish color, and it experienced a small but significant non-gravitational acceleration on its way out.

For over a year, I was very enthusiastic about the possibility that ‘Oumuamua’s properties could be explained by appealing to a composition rich in molecular hydrogen ice. Darryl Seligman and I published a paper outlining this idea, which generated a fair amount of interest in the wider media. Last year, however, Yale graduate student Garrett Levine carried out a very detailed investigation to trace how macroscopic objects rich in molecular hydrogen ice might form in the cores of the densest, coldest molecular clouds. Our final conclusion was that while it’s not impossible, it’s very difficult for the present-day Universe to manufacture solid H2. The microwave background temperature just isn’t quite cold enough yet…

Recently, Metaculus (which has been undergoing rapid development) launched an on-line journal featuring fortified essays in which an in-depth article on a topic of interest is linked to a set of questions on which readers can predict. Garrett wrote an essay the outlines the future detection and research prospects for ISOs. Everyone’s encouraged to read it and place predictions.

Music from your formative years stays with you — generally in latent form, but at other times echoing resurgently through the amorphous cycles of nostalgia that stretch out into decades.

For me, it was the era of The Sisters of Mercy, New Order, The Psychedelic Furs, and Depeche Mode. Listening to the old LPs sometimes occasions a near-electric jolt when stanzas that seemed obscure are suddenly infused with stunning up-to-the-moment relevance. Stuck inside of Memphis with the mobile home, sing…

Several days ago, I noticed a new Metaculus question with a curious, almost clickbait-worthy title, When will we meet grabby aliens?

The reference is to a recent paper by Hanson, Martin, McCarter and Paulson that has been getting traction in response to write-ups by Scott Aronson and others. Hanson et al.’s abstract rebrands as “grabby”, a subset of extraterrestrials that would appear to bear certain similarities to the antagonists in Starship Troopers.

The parameters of the GC model determine how fast and in what manner space-time fills up with grabby civilizations, and are specified by (1) the rate at which grabby civilizations emerge, (2) the rate at which they expand, and (3) the number of “hard steps” (bottlenecks) in the so-called Great Filter, whatever it is that prevents non-living matter from making the transition to living matter.

The Hanson et al. abstract strikes me as a more or less point-by-point rephrasing of Everything Counts by Depeche Mode. Aside from the line about Korea (maybe misheard along the lines of “Here we are now in containers”?) everything in the song is fully relevant.

The grabbing hands grab all they can
All for themselves, after all
It’s a competitive world

Given the model assumptions, grabby civilizations blister out within the universe in a manner determined by the values of the three parameters. The paper has an attractive figure that illustrates one particular outcome, with 193 randomly candy-coated GCs appearing over several Hubble Times across a 2D slice 41.7 billion light years on a side.

The paper’s take-away argument is that we’re living at some point in the clear space above the GC surfaces, and at some point in the future we’ll either become a GC or we’ll be steamrolled by one. Moreover, it’s argued that at the present moment, it’s likely that a “third to a half of the universe is within grabby-controlled volumes.” Hmm.

The Metaculus question asks for predictions of the probability distribution over the number of years before we or our descendants encounter a GC. At the moment, the median of the community PDF is a staggering 22.7 billion years, with a significant peak at 2 billion years. Clearly, the emerging consensus is that this question might take a while to resolve.

Herman Bondi, Tommy Gold and Fred Hoyle’s steady state theory of cosmology introduced the so-called perfect cosmological principle, which holds that the universe is homogeneous and isotropic in both space and time. Two papers outlining the their theory appeared in 1948, and maintained considerable influence until evidence that the Big Bang occurred became incontrovertible. A satisfying anecdote relates that the steady-state theory was inspired by the circular plot of the British post-war horror film, The Dead of Night.

If a horror movie can act as the aesthetic pivot for a debunked cosmological theory, it stands to reason that Depeche Mode may have pointed toward the resolution of the Fermi Paradox. The key lies in the fact that if it’s a competitive world, then

Everything counts in large amounts.

When one talks about aliens and grabby extraterrestrial civilizations, one is really talking about computation. And if grabby computation is irreversible and device-based, then planets are really nowhere. They just don’t matter. A wind of catalyzed nano-devices within the outflow from a single dust-spewing extreme asymptotic giant branch star can accomplish of order 10^62 bit operations, a factor of ten million times more than a “habitable” planet can muster over 5 billion years if totally covered with solar panels. Again, when it comes to the big picture, planets are completely irrelevant.

Here’s a link to our working paper, The Black Clouds, which discusses how extreme Asymptotic Giant Branch stars can be commandeered in the service of computation. We might just be immersed in a colored region, and the WISE sources in the Mollweide projection above might just be our unfriendly local GC.

Or, as the song says,

Confidence taken in
By a suntan and a grin.

A few years ago, I put up several posts describing Metaculus, the online prediction site that I co-founded with Anthony Aguirre and several other partners. In the interim, the site has grown substantially. It’s now logged roughly half a million predictions from a community of more than 10,000 users on a panoply of nearly 7,000 questions. Among the subset of binary questions that have resolved, the track record shows that Metaculus’ Brier Score stands at an impressive 0.117.

As the site has grown we’ve added staff, including a full-time CEO and a CTO, and a roster of analysts and question writers. We’re running real money competitions, including a $50K forecasting tournament on topics related to the development of artificial intelligence.

Many oklo.org readers may find interest in the Fermi-Drake question series, where we’re accumulating predictions on the terms of the famous equation for N.

Beyond N, there are many active questions that touch on astrophysical topics.

including the ultimate question:

currently registering a 71% probability of resolving positively.

Writer’s block. Procrastination. Envy of those for whom words flow smoothly! Luxurious blocks of text. Paragraphs, Essays, Books.The satisfying end results of productivity made real.

Or, as Dorothy Parker put it, “I hate writing, I love having written.”

Over the past few years, this dynamic has kept me both keenly and uneasily interested in natural language generation — the emerging ability of computers to produce coherent prose. In a post that went up just under four years ago, I reported on experiments that used Torch-rnn to write in the vein of Oscar Wilde and Joris-Karl Huysmans, the acknowledged masters of the decadent literary style. A splendidly recursive quote from the Picture of Dorian Gray has Wilde describing the essence of Huysmans’ A Rebours.

Based on a 793587-character training set composed of the two novels, 2017-era laptop-without-a-GPU level language modeling — which worked by predicting the next character in sequence, one after another — could channel the aesthetic of décadence for strings of several words in a row, and could generate phrases, grammar and syntax more or less correctly. But there was zero connection from one sentence to the next. The results were effectively gibberish. Disappointing.

In the interim, progress in machine writing has been accelerating. Funding for artificial intelligence research is ramping up. Last year, a significant threshold was achieved by GPT-3, a language model developed and announced by OpenAI. The model contains 175 billion parameters and was trained (at a cost of around $4.6M) on hundreds of billions of words of English-language text. It is startlingly capable.

A drawback to GPT-3 is that it’s publicly available only through awkward, restrictive interfaces, and it can’t be fine-tuned in its readily available incarnations. “A.I. Dungeons” anyone? But its precursor model, the 2019-vintage GPT-2, which contains a mere 1.5 billion parameters, is open source and python wrappers for it are readily available.

For many years, oklo.org was primarily devoted to extrasolar planets. Looking back through the archives, one can find various articles that I wrote about the new worlds as they arose. One can also look back at contemporary media reports of the then-latest planetary discoveries. Here’s a typical example from a decade ago, the beginning of an article written by Dennis Overbye for the New York Times.

In collaboration with Simone Williams, a Yale undergraduate student, we scraped the media archives from the past two decades to assemble a library of news articles describing the discovery of potentially habitable extrasolar planets. Once all the articles were collected, we developed a consistent labeling schema, an example of which is shown just below. The Courier-font text is a summary “prompt” containing the characteristics of the planet being written about, as well as a record of the article’s source, while the Times-font text is the actual article describing an actual detected planet (with the title consistently bolded in san serif). In this case, it’s another piece by Dennis Overbye from 2007 reporting Gliese 581 c:

A benefit of the GPT series is that they are pre-trained. Fine tuning on the corpus of articles takes less than an hour using Google cloud GPUs.

And the result?

Here’s an imaginary article describing the discovery of a completely manufactured planet (albeit with a real name) with completely manufactured properties.

It’s definitely not perfect, but it’s also not that bad…

East Rock rises abruptly from the flat New Haven city streets that surround it. Approaching from the south or the west, its diabase ramparts rear up forbiddingly.

While most of the East Coast’s ranges date to the continental collisions that assembled Pangea, the igneous intrusions and the sedimentary rocks of central Connecticut are roughly half as old and stem from Pangea’s demise. East Rock Park is a Jurassic Park, and two hundred million years ago, the rifts that eventually grew to become the Atlantic Ocean were opening just south of town. The rift valley floor was sinking, sediment was accumulating to fill the growing depression, and the sill of lava that eventually solidified into East Rock was squeezing out in a thick viscous sheet.

Several miles north of East Rock, an extensive road cut reveals layers of sediment from near the Jurassic-Triassic boundary. Beds of reddish sandstones and fused conglomerates of mud and pebbles are tilted at an angle of about 10 degrees, a remnant of the sinking and foundering that the rock layers suffered after they formed. The strata are varied and clearly visible, representing sediments that accumulated in a rift valley that alternated between a seasonal playa during dry periods and long-lived lake bed during wet periods.

Near the dawn of the Jurassic, New Haven was located in the tropics. During rain-soaked epochs, the shores of the rift lakes were a year-round riot of green with pterosaurs soaring in the skies. Perhaps there was nothing overt in those long-departed scenes to suggest that the end-Triassic extinction was either near or was already underway. And now, two hundred million years later, the layered record of ancient climate change stands mute and unvarying as the engines of loaded dump trucks roar and strain against the freeway grades.

A close look at the road cut shows a banding pattern that starts to repeat as one ascends from the lower exposed layers at the left of the photo to the upper exposed layers on the right. A look at the literature indicates that the rate of deposition in Central Connecticut 200 million years ago was about 1 millimeter of sediment per year, so the span recorded in the exposure is about 20,000 years. The repetition reflects one precession cycle of Earth’s spin, which dictates how the seasons align with the varying distance from the Sun stemming from the eccentricity of Earth’s orbit.

The sedimentary record in the New Haven area from the period of Pangea’s rifting is continuous over something like 20 million years, and the tilted layers of rocks fill Connecticut’s central valley to depths measured in miles. Cores drilled through this colossal lens of sediment reveal that Earth’s ancient orbital eccentricity variations are faithfully recorded in the strata.

In the course of an afternoon, with a laptop and the Rebound code, one can integrate the full Solar System back to the moment when the hardened lava that makes up present-day East Rock was glowing toothpaste-red and pushing its way into the then-newly lithified strata.

Looking back over the past five million years, Earth’s secular eccentricity variations are plainly apparent. In particular, the ~400 kyr envelope produced by the beating of the Venus-dominated g₂~7.2”/yr and Jupiter-dominated g₅~4.3”/yr secular frequencies is clearly visible.

This ~400 kyr (or more precisely, 405 kyr pattern) has been remarkably stable over Earth’s history. Running the clock back to the dawn of the Jurassic 200 million years ago, it shows no real change in character from the present. The plot just below runs for 10 million years forward from the formation of East Rock. A low-pass filter has been applied to the full eccentricity variation (shown by the light orange curve) to show the 400 kyr variation swinging up and down. Just as it does today.

In the late 1950s, orbital measurements of the Martian moon Phobos were interpreted to suggest that the satellite’s orbit was decaying faster than expected. This prompted the Russian astrophysicist Iosef Shklovsky to propose a “thin sheet metal” structure for Phobos, thereby explaining its anomalous acceleration and implying that it is of artificial origin.

The ensuing jolt of public interest in this hypothesis spurred an invigorating side-line for Shklovsky, who progressed from a drably monochrome list of equation-heavy papers — replete with sober titles such as On the Nature of the Fine Structure of Emission of Active Regions on the Sun — to glamorously teaming up with Carl Sagan to (among other things) advocate examination of “paleocontact” with extraterrestrials and for scrutiny of myths and religious lore for indications of influences from out there.

My guess is that it’s quite likely Shklovsky was well aware that promoting a field that later generated efforts such as Erich von Daniken’s Chariots of the Gods, and the History Channel’s Ancient Aliens was largely just for fun. There is, after all, no harm in broadening the public’s exposure to a wide variety of ideas. Right?

As described on his Wikipedia page, on the occasion of a visit to the Berkeley Astronomy Department, Shklovsky was memorably asked by a graduate student if UFO sightings are as common in the Soviet Union as in the United States.

“No,” he replied. “In this area the Americans are far more advanced than us.”

Last weekend, there was an engrossing article in the New York Times.

Titled, ‘A Frankenstein’ that Never Lived, the piece’s top-line summary runs, “On Jan. 4, 1981, the effects-heavy production opened and closed on the same night. Forty years later, the creators revisit a very expensive Broadway flop.”

According to the article, prior to the open, hopes for success of the big-budget enactment of Mary Shelley’s 1818 classic had run high, but the show’s prospects were dashed in large and immediate measure by Frank Rich’s dreadful review in the Times. Rich’s write-up brims with both arch sarcasm and gut-punch lines such as, “we feel nothing except the disappointment that comes from witnessing an evening of misspent energy.” Reading the article, I can feel a queasy, visceral sympathy for everyone who worked on that production.

At the end of the last century, Fred Adams and I were riding high on our forecasts for the denouement of the entire cosmos. Our trade book — The Five Ages of the Universe — had, to our great thrill, just been published by an imprint of Simon and Schuster, and we were enjoying the modest acclaim that had proceeded from dividing the entire past and the entire future of the Universe into five thumbnail-friendly eras of time.

The sales, the buzz, and the idle dreams of pop-culture stardom all came to a crashing halt from one day to the next when the New York Times ran its review of our book. I can recall the sinking feeling at the moment when our agent called Fred to let us know what had happened. “Brace yourself.” I think that was what she said.

Dick Teresi’s review was entitled, “The First Squillion Years”, and the title telegraphed the intent. It starts out bad, it gets progressively worse, and finally ends rather crushingly, with “Imagine an astronomer looking back at us ages hence. Perhaps he can read the bound galleys in my hand. Maybe he will be kinder than I have been here.” Yikes.

It’s amazing, however, how quickly one recalibrates. The book tour that had been in the cards was scaled way back to a handful of local appearances, with Borders Books in Ann Arbor standing in as the high point. Sales dried up. Just like that, I was back to trying to find bugs in Fortran codes. Over time, it became clear to me that it was almost certainly just as well.

Rather amusingly, the distant future is currently having something of a moment. There have been several new trade books on the topic, including at least one that got a review in the Times that was entirely different in tone that the one we drew. And then, a fantastic coda for the whole episode arrived unexpectedly a week or two ago as I was leafing through a recent issue of the New Yorker.

I’ve always enjoyed Roz Chast’s cartoons. She has a great sense of humor. It was oddly gratifying to see that she’d somehow been seized to lift out our eras and our thumbnails, elevating them to a full-page cartoon.

Time has a way of sliding by. More than five years ago, I wrote a blog post with a suggestion for a new cgs unit, the oklo, which describes the rate per unit mass of computation done by a given system:

1 oklo = 1 bit operation per gram per second

With limited time (and limited expertise) it can be tricky to size up the exact maximum performance in oklos of that new iPhone 12 that I’ve been eyeing. Benchmarking sites suggest that Apple’s A14 “Bionic” SoC runs at 824 32-bit Gflops, so (with Tim Cook in charge of the rounding) an iPhone runs at roughly a trillion oklos. Damn.

Computational energy efficiency also keeps improving. Proof-of-work based cryptocurrencies such as Bitcoin have laid the equivalency of power, money and bit operations into stark relief. The new Antminer S19 Pro computes SHA-256 hashes at an energy cost of about one erg per five million bit operations, a performance that’s only six million times worse than the Landauer limit. There is still tremendous opportunity for efficiency improvements, but the hard floor is starting to come into view.

For over a century, it’s been straightforward to write isn’t-it-amazing-what-they-can-do-these-days posts about the astonishing rate of technological progress.

Where a calculator like ENIAC today is equipped with 18,000 vacuum tubes and weighs 30 tons, computers in the future may have only 1000 vacuum tubes and perhaps weigh only 1½ tons.

And indeed, there’s a certain intellectual laziness associated with taking the present-day state-of-the-art and the projecting it forward into the future. Exponential growth in linear time has a way of making one’s misses seem unremarkable. “But I was only off by a few years!”

Fred Adams was visiting, and we were sitting around the kitchen table talking about the extremely distant future.

We started batting around the topic of computational growth. “Given the current rate of increase in of artificial irreversible computation, and given the steady increase in computational energy efficiency, how long will it be before the 10¹⁷ Watts that Earth gets from the Sun is all used in service of bit operations?”

As with many things exponential, the time scale is startlingly sooner than one might expect: about 90 years. In other words, the long-term trend of terrestrial economic growth will end within a lifetime. A computational energy crisis looms.

In any conversation along such lines, it’s a small step from Dyson Spheres to Kardashev Type N++. If you want to do a lot of device-based irreversible computation, what is the most effective strategy?

A remarkably attractive solution is to catalyze the outflow from a post-main-sequence star to produce a dynamically evolving wind-like structure that carries out computation. Extreme AGB (pre-planetary nebula phase) stars have lifetimes of order ten thousand years, generate thousands of solar luminosities, produce prodigious quantities of device-ready graphene, and have photospheres near room temperature.

We (Fred and I, along with Khaya Klanot and Darryl Seligman) wrote a working paper that goes into detail. In particular, the hydrodynamical solution that characterizes the structures is set forth. We’re posting it here for anyone interested in reading.

As we remark in the abstract, Possible evidence for past or extant structures may arise in presolar grains within primitive meteorites, or in the diffuse interstellar absorption bands, both of which could display anomalous entropy signatures.

For well over a year now, oklo.org has languished on Bluehost’s servers. No new posts. No maintenance whatsoever. The PHP installation was so dated that for months, visits to the site received nothing but a cryptic SQL fail. An hour with technical support was sufficient to bring the site back up, but the result was disheartening. The URL was landing hard, with an insecure SSL warning, a creaky WordPress theme that shouted “mid-aughts”, and an alarmingly wanton disrespect for the aspect ratios of the once-carefully embedded images.

New decade. New resolve.

The name on the site header now matches the site URL. Systemic referred to the long-lapsed Systemic Console project which Aaron Wolf and I started in 2004. Later, Stefano Meschiari took over the code base, and developed the software to pearlescent degrees of refinement. Yet the intangibles that generated the thrill in the Doppler velocities have all but faded, now that an essentially Earth-mass planet orbits at an essentially temperate distance from Proxima Centauri, and rumors circulate of a signal of order a GHz rather than a meter per second.