Saturn’s polar axis is tilted relative to the plane in which Saturn orbits the Sun, and the plane of Saturn’s orbit is itself tilted with respect to the averaged orbital plane of the Solar System’s planets.

Pieces of popular scientific writing often start with an engaging “hook”, but the foregoing statement doesn’t do a particularly good job. Saturn and its rings do, however, do a good job of showing off their tilts — their obliquities, to use the vernacular. Saturn gradually shifts in appearance as the Sun’s illumination angle changes, and over time the creeping ring shadows even affect Saturn’s climate. Certainly, at the moment when the rings slice edge-on to the solar rays, the system presents a very different appearance than when the ring plane is inclined.

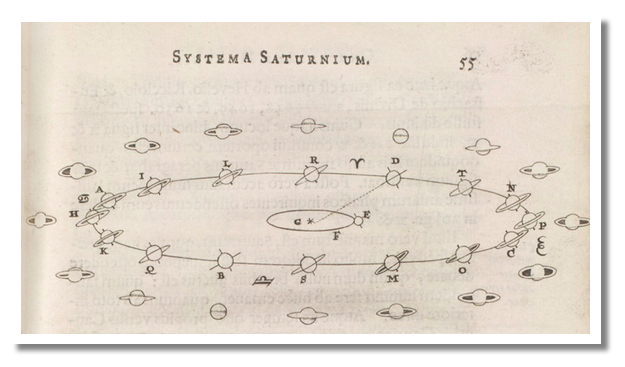
The geometry was first understood by Christiaan Huygens. By the mid-1600s, he had drawn a clear diagram showing how Saturn’s tilted pole points in a fixed direction as the planet traces its three-decade orbit.

The obliquities of Saturn and Neptune (26.7\(^{\circ}\) and 29.6\(^{\circ}\) respectively) seem odd. Uranus, tipped to its side and then some (97.9\(^{\circ}\)) is odder still. Naively, one might have expected a Solar System forming from a flat, orbiting disk of gas and dust to have ended with the equators of the giant planets lying in the average plane of the planetary orbits. Jupiter, with its axis tilted at only 3.1\(^{\circ}\) is indeed fairly conforming, but the others are all badly out of alignment. Why?

Moreover, with literally thousands of worlds now in the catalog, one also wonders if spin misalignments are rampant among the extrasolar planets. Could it be possible to infer obliquities even if we have no method to photographically resolve the planets themselves?

Left to orbit freely around a star, the tilted spin pole of an isolated planet will precess like a gyroscope. The cycling of precession is slow in comparison to the rate of the spin itself, and it stems from the torque exerted on the planet by the parent star. If the planet — like Saturn — has satellites, they orbit quickly enough to act as if they were a contributing part of the planet, and the joint set-up of planet plus moons precesses as a unit. The moons and rings stay locked to the orbital plane, and the net effect of the satellites, as far as precession is concerned, is to speed up the rate at which the cycle occurs.

Wheels within wheels… The situation grows more complicated if the orbital plane of a precessing planet also precesses. An orbit whose own pole (or orbit normal) traces a slow overhead circle presents, in effect, its planet with a moving target. With the complication induced by the precessing orbit, how does the spin axis respond?

Some intuition can be obtained by experimenting with tops. Orbital precession can be mimicked by placing a spinning top on a plate and evenly rotating the tilt of the plate, much as if panning for gold.

After some practice, one finds that the plate-top system can be transiently “locked” into a state where the spin axis precesses in the opposite direction — but at the same rate — as the plate. When this happens it’s oddly satisfying, imparting a tactile clue that resonance between the precession of an orbit and the precession of a planet’s spin might be capable of playing a dynamical role.

Another clue is supplied by the motion of Earth’s Moon. In 1693, Giovanni Domenico Cassini, who logged careful observations from the Paris Observatory, concluded that the plane of the Moon’s orbit, in the course of executing a 18.6 year precession cycle about Earth’s equator, maintains a constant angle with respect to the ecliptic (Earth’s orbital plane). He also found that the small obliquity of the moon, which is only 1.5\(^{\circ}\) (compared to 23.5\(^{\circ}\) for Earth) precesses at the same rate of one full revolution per 18.6 years.

In other words, an arrow pointing out of the Moon’s pole always lies in the plane formed by Earth’s orbit normal and the Moon’s orbit normal. This remarkable co-precession of the Moon’s spin axis and its orbit normal received little attention until a landmark 1966 paper in the Astronomical Journal by Giussepe Colombo — who separately, achieved fame for discovering that Mercury exists in 3:2 spin-orbit resonance, turning three times on its axis for every two trips around the Sun. A few years after Colombo’s paper appeared, Stan Peale coined the term Cassini State to describe the dynamical configuration.

That something so fundamental to the motion of the Earth-Moon system was left apparently unexplained from its discovery in 1693 through 1966 seemed puzzling, so I sent a text to Konstantin Batygin.

Indeed they do:

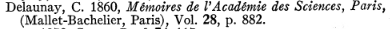
Issues of obscurity, precedence and priority aside, Colombo used Newton’s laws of motion and gravity to demonstrate that the in-sync cycling of the Moon’s spin and orbital axes represents a minimum-energy configuration. In a frame of reference synchronized to its orbital precession, the Moon’s spin pole is analogous to a marble that frictional dissipation has brought to rest at the bottom of a curved bowl. The Moon is said to be locked in a secular spin-orbit resonance.

If a perturbation — a kick — imparts energy to the marble, it will roll around in the bowl. Likewise, if the spin pole of a body in secular spin-orbit resonance is perturbed, the direction that the pole points will wander when viewed in the precessing frame. In his 1966 paper, Colombo worked out how the trajectories traced by a perturbed spin pole will behave.

Colombo also pointed out that a simple geometric construction can be used to illustrate how the spin pole moves. First, imagine the sphere defining all the possible directions that a spin pole can point. The sphere is oriented so that its own coordinate poles are perpendicular to the overall plane of the system under consideration. In the minimum energy configuration, the spin direction, the coordinate pole, and the direction of the orbit normal all lie in a single plane that slices the sphere in half.

If the planet’s spin axis is not damped to the minimum energy configuration, it will slowly trace a path on the sphere when followed in the co-precessing frame. A detailed analysis (which appears in Colombo’s 1966 paper, and which Stan Peale augmented and corrected in 1969) shows that the set of allowed paths (level curves of the Hamiltonian) are determined by the set of possible intersections between a parabolic cylinder and the sphere. Individual paths, corresponding to individual energies of perturbation, are defined by moving the parabolic cylinder back and forth.

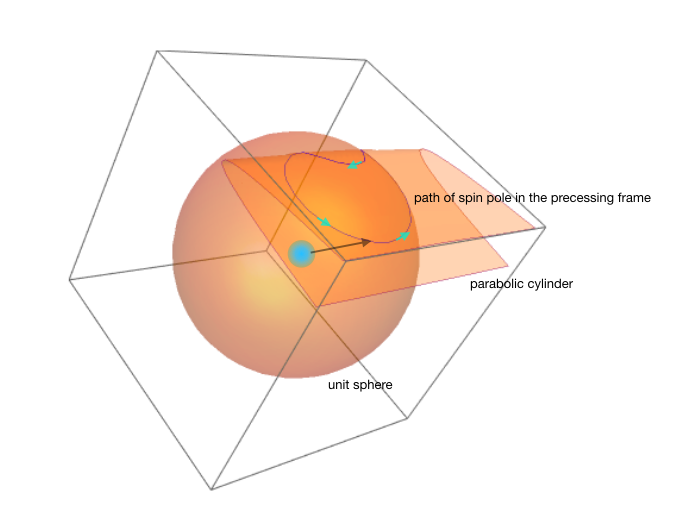
Remarkably, the projection of these intersection paths onto the ecliptic displays a characteristic structure that arises repeatedly in problems involving resonance. The state of co-precession keeps the spin pole of the planet fixed in the perfectly damped configuration, in which the vertex of the parabola just touches the sphere. This vertex point lies at the center of a set of banana-shaped trajectories. Then, when the spin pole of the planet is perturbed, the motion follows a trajectory where the spin pole travels along one of the banana-shaped curves. Inside the shaded region, a full traversal of the curve never entails a full 360\(^{\circ}\) accumulation of angle, and the pole is said to be librating in the resonance.

The Solar System provides several examples of secular spin-orbit resonance. Most prominent from our Earth-bound viewpoint, is the motion of the Moon. The action of tides has damped the motion of its spin pole so that it lies at the core of its sequence of banana-shaped level curves.In a pair of articles [1, 2] published in 2004, Bill Ward and Douglas Hamilton raised the remarkable possibility that Saturn’s spin pole might be librating in a frame that co-precesses with the orbital inclination of the planet Neptune. On the surface, a Saturn-Neptune secular spin-orbit resonance seems nearly unbelievable. I recall hearing Bill Ward describe the work at a conference, a year or so before the papers came out. At that time, I have to admit, I didn’t really understand the details of the talk, other than the the take-away that Neptune was somehow responsible for tipping Saturn over. Although Jupiter and Uranus exhibit substantially larger gravitational perturbations on Saturn than does Neptune, the frequency at which Neptune’s line of nodes regresses happens to almost exactly match the precession rate of Saturn’s pole. Neptune’s orbit, in a sense, shifts at a rate that cuts through the noise to provide a controlling influence that adds up for Saturn.

Once the precession rates of an orbit and a spin pole are locked together, the lock will be maintained even when the orbit’s precession rate slowly changes. As a consequence, if the rate at which the orbit precesses slows down, the planet’s spin pole will slowly tip over so that its precession rate can decline in sync. When that happens on a habitable planet, it’s time to set solar sail for the stars. Closer to home, the long-ago dispersal of planetesimals in the Kuiper Belt led to a slowing of Neptune’s orbital precession. Remarkably, this seemingly minor slowdown seems to have forced Saturn from a small initial obliquity to its current 26.7\(^\circ\).

In addition to affecting Earth’s Moon and Saturn, secular spin-orbit resonance also plays a likely role in the tilts of both Jupiter and Mars (and quite possibly Uranus). It’s fully separate from the phenomenon of spin-orbit resonance, which, for example, maintains Mercury’s spin period at an average rate that is exactly 3/2 times its orbital period.

In the Solar System, the planetary obliquities are readily measured, and have been accurately known for centuries. Orbital precession rates can be calculated either from the well-established techniques of celestial mechanics, or from direct numerical N-body integrations. Even so, secular spin-orbit resonance didn’t garner attention until Colombo’s and Peale’s papers in the 1960s, and even then, it received only limited press. In Murray and Dermott’s Solar System Dynamics, which has become a standard text, the authors state at the outset that Cassini states are not covered in their book. The possible enforced match between Saturn’s polar tilt and Neptune’s orbit went unnoticed until 2004. It thus seems like a long-shot that secular spin-orbit resonances among extrasolar planets have much chance of being a “thing”.

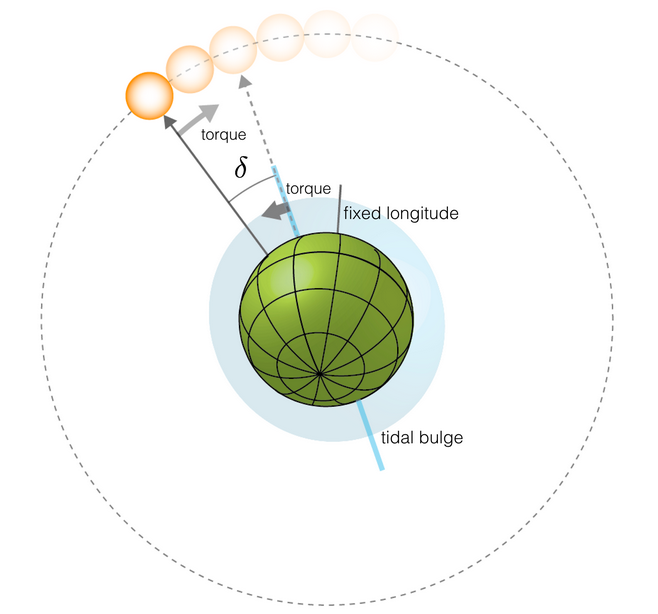
For a planet like Saturn, the slight decrease in the Sun’s gravity from the sub-solar point to the anti-solar point on Saturn’s surface leads to a small tidal deformation of the planet. Friction within Saturn causes Saturn’s rotation to pull this tidal deformation slightly out of alignment, with the net result being a slow decrease in Saturn’s spin rate. The rate of decrease, however, is negligible. It would take many times the current age of the Solar System for Saturn’s spin period to be tangibly modified by this effect.

Tidal forces, however, have an extraordinarily steep fall-off with distance. If Saturn were moved a hundred times closer to the Sun, to a distance where the extrasolar planets are routinely found, the Sun’s tidal influence on Saturn’s spin would be ten billion times stronger.

In the presence of strong tidal forces, the spin period of a planet on a circular or near-circular orbit is brought into sync with the planet’s orbital period. That’s the situation that the Moon finds itself in, and it is also thought to be the case for most of the shorter-period transiting planets that have been discovered by the various ground-based surveys as well as by the Kepler Mission.

In addition to synchronizing the spin, tidal forces also act to align a spin pole with the orbit normal. If, however, a planet is in secular spin orbit resonance of the type we’ve been discussing, the resonant torques can potentially balance the dissipative torques and prevent the planet from being righted.

Tidal dissipation is normally quite self-regulating. If the dissipation caused by tides is strong, then synchronization ensues, and the energy that the dissipation generates drops. If, however, a mechanism exists to thwart synchronization then significant evolution can occur. Io (and to a lesser extent Europa) provide examples. As a consequence of having its eccentricity forced by the resonant interaction between the three inner Galilean satellites, Io undergoes strong tidal dissipation, leading to the famous volcanoes that cover its surface, and to the heavy loss over time of its volatile constituents.

The famous Peale, Cassen and Reynolds article that describes Io’s dissipation belongs near the very top of a list of admired papers. It presents clean dynamical arguments that draw on disparate aspects of geophysics and celestial mechanics to make a non-trivial prediction. And indeed, the paper’s two-sentence abstract is the very model of brevity:

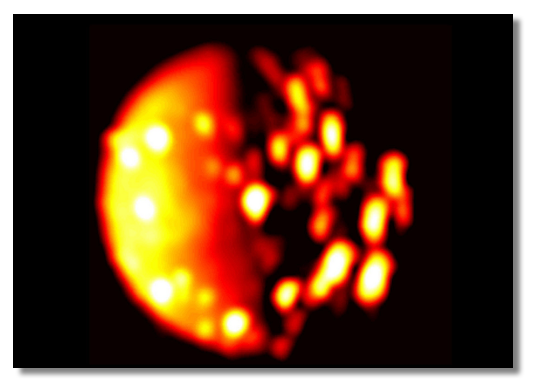
The dissipation of tidal energy in Jupiter’s satellite Io is likely to have melted a major fraction of the mass. Consequences of a largely molten interior may be evident in pictures of Io’s surface returned by Voyager I.

Just days after the March 2, 1979 publication of the paper, Voyager 1 flew through the Jovian system, and recorded Io’s hyperactive volcanism. Here’s a recent photo of Io from NASA’s Juno probe. The picture was taken in the infrared, where it’s pretty clear what’s going on.

In short, the Peale et al. 1979 paper is a tremendous inspiration. For years, I’ve been thinking, could something similar be done with the extrasolar planets?

The Kepler data is certainly the best place to look for opportunity. The precise timing of the planets in Kepler’s multi-planet systems gives the possibility for finding subtle effects that go beyond simple Keplerian orbital motion.

It’s well known that Kepler detected lots of multiple-planet multiple-transiting systems. The planets in these systems tend to lie in the super-Earth/sub-Neptune radius range, and typically have masses of order 5 to 10 times the mass of Earth. A zeroth-order question is what these planets are like and how they got to where they are currently observed.

There is an interesting unexplained clue in the data. One can take pairs of adjacent planets from the Kepler catalog, and plot the period ratios. What one sees is that in the vicinity of low-order orbital commensurabilities, there is a statistically structure in the distribution:

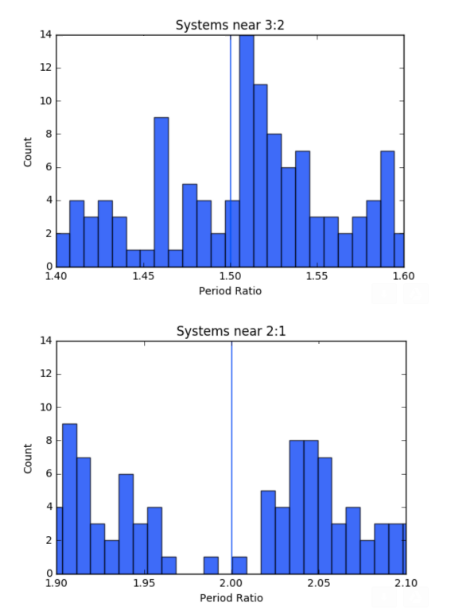
There is an overabundance, or a “pile up” of planets with orbital period ratios that are a few percent larger than the perfect 3:2 and 2:1 orbital commensurabilities, and a relative lack of planet pairs that have orbital period ratios just less than the commensurabilities. It’s as if some mechanism is acting to pry the pairs apart. Moreover, if one looks at the individual sizes of the planets in the distribution, one sees that on average, the radii of the planets that lie just wide of the commensurability are larger than the radii of the planets that have slightly smaller period ratios.

Several theorists have written papers that show this structure, termed “resonant repulsion” can be understood if the participating planets are experiencing a very high rate of tidal dissipation. The difficulty, however, has been that if the standard rate of interior energy dissipation is used, then the rate of dissipation would have to be very high. The planets would have to be extremely inelastic. Earth for example, does fall into this inelastic category because the ocean tides efficiently dissipate energy along shorelines. Most bodies in the Solar System, however, and especially the massive planets – Uranus, Neptune, Saturn and Jupiter – are far less dissipative. In the case of the Solar System’s giant planets, this difference with Earth is of order a factor of a thousand or more.

In a new paper appearing in Nature Astronomy and lead-authored by Yale graduate student Sarah Millholland, we propose a solution. If one or both planets in a pair that has a period ratio lying just outside the low-order commensurability is in secular spin-orbit resonance, and if the spin obliquity is high, then the dissipation within the planet will be large, and indeed large enough to account for the observed effect.

In many respects, the regular satellites of the jovian planets in our solar system resemble the multiple-transiting multiple planet population that was found by the Kepler Mission. Orbital inclinations and eccentricities are small in both types of systems. The orbital periods typically range from days to weeks in both cases, and the mass ratios of satellites to primaries typically tend toward one part in ten thousand. It is thus reasonable to ask why the phenomenon of resonant repulsion die to secular spin-orbit resonance is not found among the jovian satellites, all of which have tiny tilts for their spin poles.

The answer lies in the spin rates of the giant planets, all of which spin relatively rapidly, causing them to bulge significantly at their equators. Jupiter does a full turn in only 9 hours 55 minutes and is noticeably squashed when viewed through a telescope. The quadrupole moment is the jargon for the quantified degree of spin-induced structural flattening. The giant planets’ large quadrupole moments force rapid orbital precession of their satellites. The frequency is substantially higher than the spin precession rates of the satellites can keep up with. As a consequence, all of the major regular satellites of the Jovian planets have their spin axes aligned with their orbit normals.

The parent stars of the Kepler multi-transiting, multiple-planet systems spin much more slowly than Jupiter or the Solar System’s other giant planets. The stars have lost the majority of their spin angular momentum through the process of magnetic braking. The quadrupole moments of the G, K, and M stars hosting Kepler-multiple planet systems are quite small. Our own Sun spins on its axis with a 27-day period, which is fairly typical, and red dwarfs tend to spin even more slowly. As a consequence, the precession periods of the Kepler planet’s orbits are driven primarily by planet-planet interactions and not by the stellar equatorial bulges.

In the plot just below, the natural spin precession frequencies, \(\alpha\)‘s, and the orbital precession frequencies, \(\vert g \vert\)‘s, for the planets in Kepler’s multiple-transiting systems are tallied into histograms. The rate, \(\alpha\) of a planet’s spin precession depends on its internal structure, so that a planet that is highly centrally concentrated (a low \(k_2\)) precesses more slowly than one whose mass is more extended (a high \(k_2\)). The histograms for the spin and orbit rates (\(\alpha\)‘s and \(\vert g \vert\)‘s) show substantial overlap, and both reach peaks near a period of about 3,000 years.

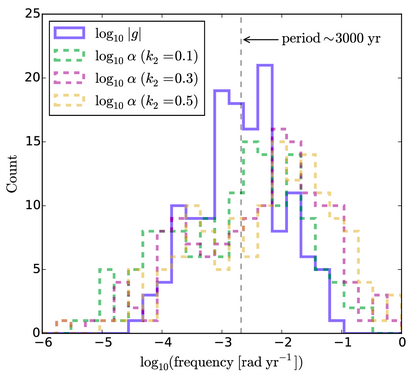
In short, it is a suggestive coincidence that the orbital periods, the masses, the radii and the separations of the Kepler planets combine to generate similar rates of orbital precession and spin precession. This means that capture into spin orbit resonances may be quite likely for these planets.

Capture of a planet into secular spin-orbit resonance will naturally occur if the ratio of the planet’s orbital precession frequency to its spin precession frequency is slowly brought down to unity from above, that is, if \(\vert g \vert/\alpha \rightarrow 1\). This can happen if the planets in a system migrate toward orbital commensurability. This schematic diagram from our paper shows how the process works:

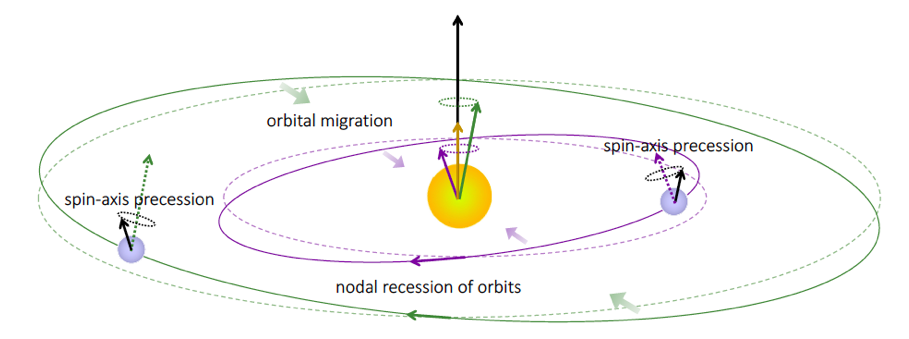
Simulations that track the orbits and the spins of the planets show that the spin precession and orbit precession lock into sync remarkably easily and naturally. Our paper charts several example evolutionary trajectories that look like this one:

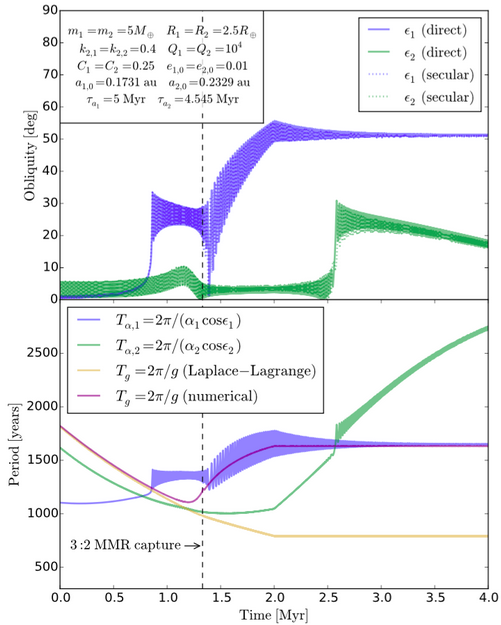
In this particular simulation, two 5 \(M_{\oplus}\) super-Earths experience mild disk-driven migration which slowly pushes their orbits together, and, after \(\sim\)1.3 million years, binds them into a 3:2 orbital mean-motion resonance. As this mean-motion resonance capture occurs, the inner planet of the pair finds that its orbital precession rate has slowed to match its spin precession rate; it is caught in secular spin-orbit resonance. Thereafter, as the orbital precession slows still further (as a consequence of the protostellar disk dissipating), the inner planet’s axis is compelled to precess more slowly as well. In order for the planet to slow its spin precession, it is forced over on its side, to a final obliquity of more than 50\(\circ\).

The simulation charted above runs for just a few million years, but the planetary systems that Kepler observed are generally a thousand times older. The outer planet in the simulation, whose obliquity is traced with the green line in the upper panel, sees its tilt kicked up when the ratio \(\vert g \vert/\alpha\) passed through unity from below but does not end up in spin-orbit resonance. Its perturbed obliquity will drop back to zero after a few tens of milions of years. For the inner planet, however, the situation is different. Torque from the tidal dissipation in the planet balances torque from the precessing orbit, the obliquity remains constant, and an Io-like situation is produced. Obliquity-juiced tides generate ~3 million Gigawatts within the planet, roughly a thousand times the total power that Io produces, and roughly three times more energy per unit mass. The relentless dissipation draws energy from the orbit, forcing the period ratio, over time, to creep up from the initial 3:2 ratio.

The net result of this process, replicated again and again in the Kepler sample, can explain the lack of worlds near the exact m:n integer period ratios and simultaneously account for the pile-ups seen just wide of the perfect commensurabilities.

A nice feature of the theory is that it makes some predictions.

,Capture into secular spin-orbit resonance is easier if a planet has a larger radius. As a consequence, if dissipating oblique planets are what drive the Kepler pairs apart, then the planets on the right side of the period ratio gaps should be (on average) larger than those to the left sides of the gap. Pleasingly, this is exactly what is seen in the data, and it’s a feature that has gone unnoticed until now:

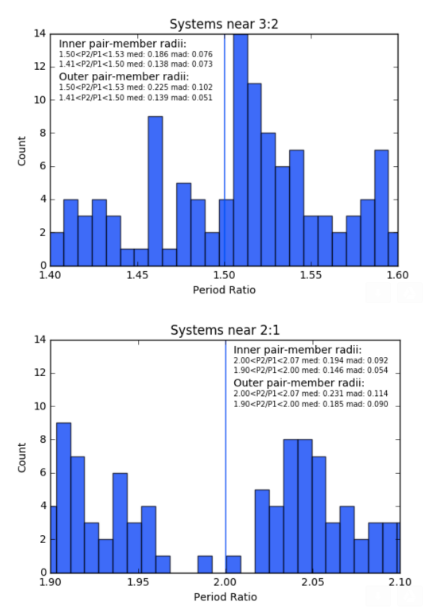
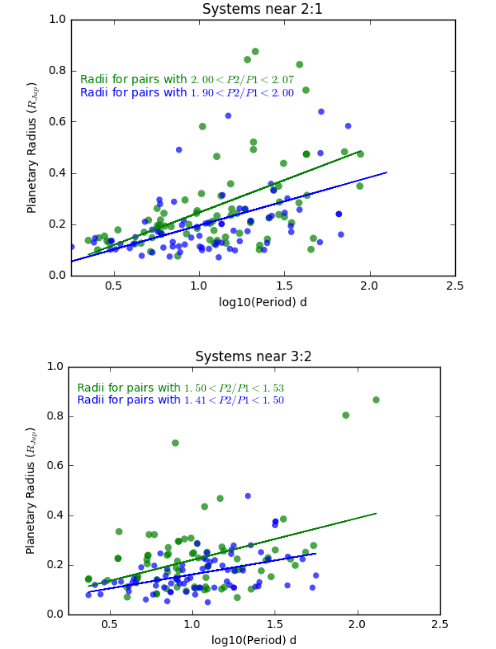
Moreover, larger planets are more dissipative, and so statistically, the radii of planets in the member pairs should increase as the period ratios increase. This effect, while subtler, is also present in the data.

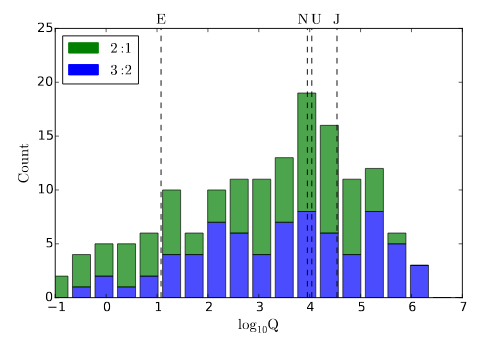
Given the actual structure of the period ratio diagram, one can work out the amount of dissipation required to explain each pair if the ages of the systems are known. Statistically, this allows us to determine what kind of planets we’re dealing with. The details are explained in our paper, but the take away is that the planets in the Kepler-multiple systems likely tend to resemble Uranus and Neptune as far as their internal structures are concerned.

And finally, one last, as-yet untested prediction. If a planet with an orbital period in the range spanned by the Kepler-multiple planet systems has significant satellites, its precession rate will be too rapid for secular spin-orbit resonance to work. As a consequence, oblique planets driving resonant repulsion won’t have significant moons of the type seen orbiting the giant planets in the Solar System.