It’s hard to miss Jupiter and Venus in the early evening sky right now, and later this week, on March 15th at 10:37 UT, they will reach an impressive conjunction, with Venus near maximum elongation (separated by 46 degrees from the Sun) and Jupiter only 3.3 degrees from Venus.
At the time of conjunction, Venus will have an apparent magnitude of V=-4.2 and Jupiter will be at V=-1.9. They are thus both brighter than Sirius, and the display is all the more impressive because the planets are still well above the horizon at the end of astronomical twilight.
The combination of the HARPS Survey and the Kepler data are indicating that the architecture of our solar system is — to at least a modest degree — somewhat unusual. If we were living in a run-of-the-mill planetary system, we could expect to have several planets with ~2x Earth’s radius orbiting with periods of 100 days or less, along with no Jupiter in a Jupiter-like orbit. A pair of standard-issue sub-Neptunes would appear substantially brighter than Venus in the dusk and dawn skies, but night-time displays as impressive as the one we’ve got now wouldn’t occur, since the maximum elongations would be ~30 degrees or less.
Jupiter’s distance from the Sun puts the regular motions of the Gallilean satellites just outside the reach of naked-eye observability, and in a similar vein, Venus’ size and semi-major axis leave it just on the threshold of displaying visible phases. If our eyes were just a little better, the “Copernican Revolution” wouldn’t be a cliche, and Archimedes would have come up with the Universal Law of Gravitation.
Our night sky does, however, give us one very nice order-of-magnitude foothold. The apparent brightness of the outermost visible planet, Saturn, falls exactly in the magnitude range populated by the brightest stars. For example, when Saturn’s rings are at a less-than-full opening angle, the planet has a nearly identical apparent brightness to Alpha Cen A. This means that if one knows the AU, has the telescopic ability to resolve the disk of Saturn, and makes the (shaky) assumption that the brightest stars are Sun-like, and the (less shaky) assumption that Saturn is highly reflective, the distances to the nearest stars can be estimated. Very roughly,
which is close to the true 4.4 light year distance. (A version of this argument was used in the late 1600s to get the first real estimate of the staggering separations between the stars.)
If one also assumes that stars travel at relative speeds that are similar to the velocities with which the planets orbit the Sun, then an extension of the ball-park argument indicates that the configuration of the night sky should be radically altered on a timescale of millions of years. This is indeed the case. There was a cool 1998 article in Sky and Telescope that used the (then-new) Hipparcos data to compute the brightest stars within the last and next five million years. At the dawn of the Pliocene era, Epsilon and Beta Canis Majoris were both of similar brightness to Venus.


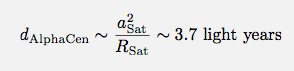
This stood out to me, though I appreciate that you qualify it:
“The combination of the HARPS Survey and the Kepler data are indicating that the architecture of our solar system is — to at least a modest degree — somewhat unusual.”
Of course, there’s a bias here — HARPS and Kepler only find the “big,” close-in planets that aren’t in our Solar System! So of course all of the systems we find will make the Solar System look unusual, by construction.
HARPS, obviously, has nothing to say about the frequency of any analogs of Solar System planets, because it is not sensitive enough to find analogs of our rocky planets (no survey but Kepler is) and has not been operating long enough to find the Jupiter analogs.
Kepler’s current data release can say something about the frequency of planets with periods of < 1 year or so, but the high photometric noise of most Solar-type stars means that even the largest of the Solar System's planets with those periods (Earth) would not have been detected yet in an Earth-like orbit (it's close, but a firm such detection will actually require an extended mission).
As best as I can tell, the Kepler frequencies are not so high as to imply that most stars host planets of the sort that Kepler is finding; is that a correct reading of your simulations with Angie?
In other words, I think that even if most stars hosted Solar System replicas, neither HARPS nor Kepler would be able to confirm or refute that fact.
Of course, if every star had a true Jupiter analog, those would be jumping out of the older surveys by now, but suppose Jupiter is just slightly atypically overweight or close-in for its class: there could be a lot of sub-Jupiters in 15-20 year orbits that are just beyond the reach of the Keck, Lick, and Swiss surveys.
On the other hand, the parameter space to "hide" lots of Solar System analogs is quickly shrinking; in the next 5 years Kepler will tell us about Venus-Earth analogs, and the RV surveys should have some good numbers on the Jupiter analogs.
@jtwright
Greg makes a convincing argument for an unusual solar system because cold Jupiters should have been detected by now and they haven’t. See here :
http://oklo.org/2011/02/13/an-analogy/
Now, if cold Jupiters are rare, so it is our solar system that spots two !
Coming to Earths, I really do not know why this isn’t discussed more widely, but Kepler data points to the rarity of Earth analogs.
Sure the raw data released are only for 16 months of observation :
http://exoplanetarchive.ipac.caltech.edu/cgi-bin/ExoTables/nph-exotbls?kepler=1
Sixteen months are 486 days.
This is equivalent for 3 periods for planets with 162 days period.
Now, what is the mass of the star that a planet with 162 days period must orbit so that it receives the same energy from the sun as Earth ?
I used these two equations :
L/Ls=(M/Ms)^4 where Ls and Ms are the mass of the Sun and L and M the ones of the star, from Wikipedia
P = 2 *pi *d/sqrt(G*M/d) where P is the period, G the gravitational constant and d the distance
I’ll spare you the intermediate passages but, according to my calculations he answer is ~0.71. So, for a any star less than 0.71 solar masses, Kepler has observed at least 3 periods of an Earth.
This looks ok because a mass of 0.71 implies a luminosity of .0254 and a distance from the star of 75.4e6 km for the same energy as the Earth. Plugging these numbers in the equation above gives a period close to 160 days.
Now, if we go back to the data, for all the stars with this or smaller mass there are Earth size planets (or similar) but all have huge temperatures.
Remember that lower luminosity stars than the sun are less noisy when transited by an Earth size planet because the planet obscures a larger portion of the disk and the signal is deeper.
You can repeat the same trick for 2periods and you get a mass of 0.84.
Again, there are Earths, just close and hot.
I do not like this data more than you do, but it looks like there’s a vacuum of Earths right in the habitable zone of lower luminosity stars. It doesn’t look good for normal G stars either.
Kepler data suggests that Nature loves “compact” systems where the planets are very close to the star, like Kepler 11.
Applying the mass-luminosity relationship for the main sequence, which is approximately 3.5 (and it’s quite a while since I did this…) A mass of 0.71 gives: 0.71^3.5 = 0.302, alternatively 0.71^4 = 0.254.
I agree with your distance of 75.4 million km (and using the ‘fourth root’ value in the mass-luminosity relationship). If we are twice as close to a star one-quarter as luminous as our sun, then we’d expect to receive about the same energy/ unit area as the earth. With the light being shifted towards the IR part of the spectrum for lower mass-stars.
We live in exciting times indeed and, in the years ahead; with a greater statistical count the picture will be clearer. The trends that are emerging may well be reinforced (or as expected, some surprises shall emege!).
@Enzo: out of interest how much data folding is required to pick an Earth-size object out of the noise? If more than 3 transits are typically required to spot an Earth in the first place it could lead to an apparent sharp drop-off in the number of Earths.
I think it is the lack of sub-neptune/superEarths that makes our solar system unusual. We grew up learning about rocky planets, and gas planets, and this big size gap in between, but in the rest of the galaxy, that size gap doesn’t exist- those are the most common planets everywhere else.
@pete j
I used ^4 instead of ^3.5 because the Wikipedia article said that it was more accurate fro star with mass between 0.43 and 2 solar masses.
@andy
I do not know but I know that the primary mission of Kepler is 3.5 years and, since one of their objective was to obtain statistics of the number of Earths around G stars, I assume that the Kepler team has done a pretty good analysis on this. If 3 periods are not sufficient then the primary mission of Kepler is too short. Kepler page mentions that “4 transits are required and hence the 3.5 years number”. A statement I do not understand because 4 transits would require 4 years, not 3.5, at least in 50% of the cases.
@Enzo: there was a news release a while back that the stars are noisier than had been predicted at the outset of the mission and that an extended mission will be required to get down to Earth mass planets around solar-type stars.
I’d be very careful about the statistical extrapolation of the Kepler results, there may be interesting properties in how complete the sample is. Furthermore they may well have removed some of the more interesting candidates from the public list: I noticed already that the Kepler-34 and Kepler-35 circumbinary planet systems are not listed there (Kepler-16 is in the list, so it isn’t as if the circumbinary nature is an exclusion factor)
This may be a nit pick, but do giant stars like Epsilon and Beta Canis Majoris maintain constant luminosity for 4-5 million years?