The long-term stability of the planetary orbits has been a marquee-level question in astronomy for more than three centuries. Newton saw the ordered structure of the solar system as proof positive of a benign deity. In the late 1700s, the apparent clockwork regularity of interaction between Jupiter and Saturn helped to establish the long-standing concept of Laplacian determinism. In the late Nineteenth Century, Poincaré’s work on orbital dynamics provided the first major results in the study of chaotic systems and nonlinear dynamics, and began the tilt of the scientific worldview away from determinism and toward a probabalistic interpretation.

In the past ten years, it has become fairly clear that the Solar System is dynamically unstable, in the sense that if one waits long enough (and ignores drastic overall changes such as those wrought by the Sun’s evolution or by close encounters with passing stars) the planets will eventually find themselves on crossing orbits, leading to close encounters, ejections and collisions. The question has shifted more to the following: What (if any) chance is there that the planets will experience orbit crossings within the next 5 billion years?

It’s clear that the probability of the planets going haywire prior to the Sun’s red giant phase is pretty small. Computers are now fast enough to integrate the eight planets forward for time scales of ten billion years or more. Konstantin Batygin, a UCSC physics undergrad who has been collaborating with me, has been running a suite of very long term solar system integrations, and he’s been getting some nice results.

It’s well known that over the long term, the planetary orbits are chaotic. The Lyapunov timescales for the planetary orbits in both the inner and the outer solar system are of order a few million years, which means that for durations longer than ~50 Myr into the future, it becomes impossible to make a deterministic prediction for exactly where the planets will be. . We have no idea whether January 1, 100,000,000 AD will occur in the winter or in the summer. We can’t even say with complete certainty that Earth will be orbiting the Sun at all on that date.

We can, however, carry out numerical integrations of the planetary motions. If the integration is carried out to sufficient numerical accuracy, and starts with the current orbital configuration of the planets, then we have a possible future trajectory for the solar system. An ensemble of integrations, in which each instance is carried out with an unobservably tiny perturbation to the initial conditions, can give a statistical distribution of possible long-term outcomes.

Here’s a time series showing the variation in Earth’s eccentricity during a 20 billion year integration. In this simulation, the Earth experiences a seemingly endless series of secular variations between e=0 and e=0.07 (with a very slight change in behavior at a time about 10 billion years from now). The boring, mildly chaotic variations in Earth’s orbit are mostly dictated by interactions with Venus.

Mercury, on the other hand, is a little more high-strung.

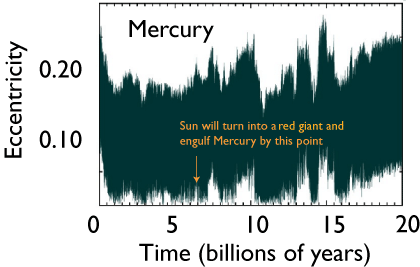
These two plots suggest that the Solar System is “good to go” for the foreseeable future. Indeed, work by Norm Murray and Matt Holman suggests that the four outer planets have a dynamical lifetime of order one hundred quadrillion years. Work by Jaques Laskar, however, suggests that the inner solar system might be on far less stable footing. Konstantin has obtained some very interesting new results on this particular point, which we’ll be sharing in an upcoming post…