Image Source.

Stefano and Eugenio have been making quite a bit of development progress on the downloadable systemic console. A new version of the console (available for beta testing on the systemic backend) is now capable of providing an estimate of the uncertainties on the orbital elements associated with a fit to a particular data set.

Radial velocity data don’t provide an exact determination of planetary orbits. The most obvious shortcoming is that Keplerian orbital fits can’t determine the inclination of the planetary orbits, and so for a given system, we’re only able to measure then mass of the planet multiplied by the sine of the unknown inclination angle. Furthermore, the stellar radial velocity signal created by a planetary system is corrupted by astrophysical noise introduced by the parent star, as well as by noise introduced during the measurement process here on Earth.

Determination of the true uncertainties in a planetary orbital model is a subtle problem (for more detail, see Eric Ford‘s recent work in this area). As a first straightforward step, we’ve implemented the so-called “bootstrap” method of error estimation into the console. The bootstrap works by taking the original data set, and then successively redrawing time + velocity + uncertainties triples from the data with replacement. This procedure creates alternate realizations of the original data set in which some of the original measurements appear more than once, and in which some don’t appear at all. The best-fit parameters obtained by the console are then used as a starting guess to fit the bootstraped data sets. The standard deviations measured from the distributions of orbital elements thus obtained give error estimates for the parameters of the original fit.

The bootstrap routine is menu-accessed, and is simple to use. First, create a fit to a dataset. In the example just below, I’ve fitted to the data for HD 80606:

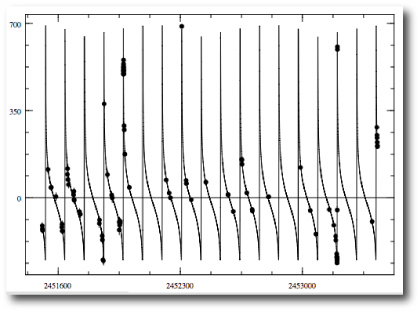
Once the fit has been polished, the bootstrap can be run. In the default configuration it uses Keplerian fitting and does 100 trials.

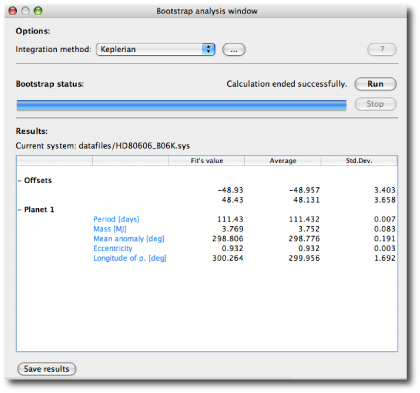
HD 80606 has been observed for nearly 20 orbital periods, and velocities have been obtained at a wide variety of orbital phases. As a result, the orbit is very well constrained. The bootstrap indicates that the uncertainty on the e=0.932 eccentricity is only 0.003. For other systems, such as hd 20782, which also seems to have a high eccentricity:

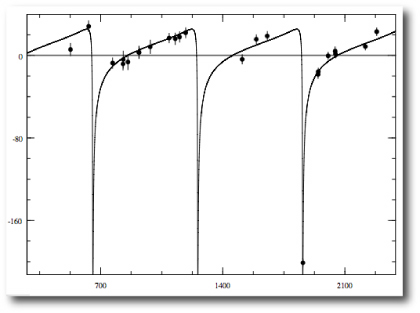
the uncertainty on the parameters is much larger:

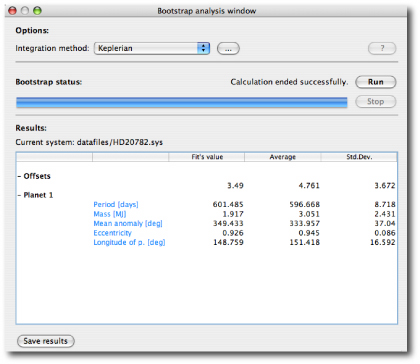
Give the routine a try! In upcoming posts, we’ll talk more about how uncertainty estimates will be incorporated into the planetary catalogs on the backend.