
Image Source.
If you’re a new visitor to the site, welcome aboard! Yesterday’s post talks about the systemic collaboration, and gives an overview of how you can participate.
The interpretation of radial velocity data sets is confounded by the existence of many different model planetary systems that all do a good job of fitting the data from a given star. If you really want to know whether a particular fit is the correct interpretation of the system, then you need to wait for (or make) more observations to see if your fit’s predicted radial velocity curve is confirmed.
For a real planetary system orbiting a real star, it can take years for enough confirming observations to be made, and so it’s useful to have as many criteria as possible for evaluating whether a particular fit is a contender. Orbital stability provides one such criterion.
On the backend, there are many orbital models that have been submitted that give excellent fits to the given data sets. For example, the four configurations shown in the picture just below are all acceptable models for the 14 Her system.
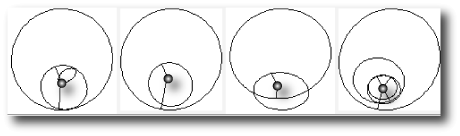
One immediately notices that these orbital configurations look “crowded”. The orbits make close approaches and sometimes even cross. If we let these model systems run forward in time, then we find that the mutual gravitational pulls between the planets lead to catastrophe within a few decades or less. Instead of behaving in an orderly fashion, the orbits execute motions like this:
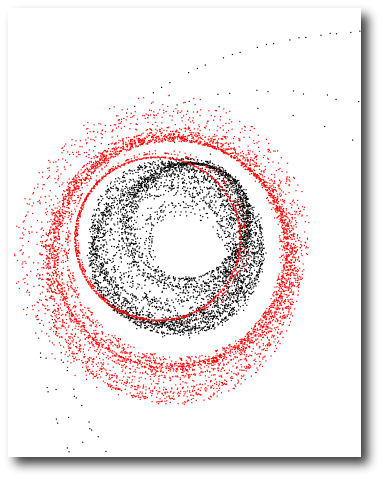
which lead inevitably to collisions and ejections. While it’s theoretically possible that we happen to be observing a particular system just before it experiences disaster, Occams razor strongly suggests that wildly unstable fits are likely spurious. We can safely exclude any configuration that lasts for only a tiny fraction of the stellar ages (which are generally in the 2-10 billion year range).
Participants in the systemic collaboration can evaluate the stability of their models by using the “check long-term stability” function on the console. Stefano has also recently implemented a robot that crawls through the systems residing in the backend database and integrates all of the submitted fits. So far, it has sorted out which systems are unstable on timescales of less than a century, and as time goes on, it’s pushing the integration times to longer horizons. It turns out that a 100-year integration can catch a majority of the systems that eventually go unstable. After that, we expect roughly equal numbers of systems to be lost in each factor-of-ten increase of integration time.
Although we don’t expect to see orbital instabilities play out on our watch, it’s nevertheless likely that planet-planet interactions and their associated instabilities have played an important past role in sculpting the systems that we now observe. For example, Eric Ford and his collaborators have published a highly plausible theory for the formation of the Upsilon Andromedae planetary system that involves a dramatic instability. In their scenario, the system starts out with four planets, and eventually ejects one of them. The outer two survivors are left stunned and reeling, and the dynamical imprint of the disaster survives to the present day. They’ve made an engaging animation (available here) that shows the action blow-by-blow.
This brings up a relevant question. If orbital instability exists among the extrasolar planets, might our own solar system eventually go unstable? Is it possible that Earth will find itself getting dramatically tossed around the solar system in the manner that was experienced by the unfortunate Upsilon Andromedae E?
The question isn’t new, and the stability of the solar system has been at the forefront of interest for the last 350 years. It was first tackled by Newton, who wanted to understand how the orbits of the Jupiter and Saturn would behave over long periods if their mutual interactions were taken into account. Newton put a lot of effort into the problem, and eventually decided that:
To consider simultaneously all these causes of motion, and to define these motions by exact laws admitting of easy calculation exceeds, if I am not mistaken, the force of any human mind.
Newton’s fame, and the fact that he’d written off the problem as too difficult, was a big motivation for succeeding generations of mathematicians. Pierre Simon de Laplace eventually solved the problem of the motions of Jupiter and Saturn, and fully explained their orbits to the accuracy that could be observed in the late 1700s. In Laplace’s model, the solar system is completely stable, and the inherent predictability of his planetary motions contributed to the concept of a rational determinism, and the idea of a clockwork universe.
During its first three hundred years, the problem of the stability of the solar system was attacked using pen and paper. In the past few decades, however, the advent of computers has provided a powerful new tool. We can now make accurate simulations of the trajectories of the planets through space, and look in detail at the solar system’s possible futures. By the 1980s, when hardware and algorithms had progressed to the point were it was possible to integrate the planets millions of years forward into the future, it was found that the solar system is chaotic in a sense originally envisioned by Poincaré. If the position of a planet, the Earth say, is given a tiny change in the computer, then as millions of years elapse, this slight perturbation grows erratically larger. If Earth is displaced in its orbit by a centimeter, then, after several million years, Earth will likely be located somewhere within 2 centimeters of where it would have been had it been given no push at all. After several million years, the degree of uncertainty doubles again, this time to 4 centimeters.
Worrying about such tiny buildups of uncertainty in the position of Earth on its orbit sounds utterly absurd. Nevertheless, like interest compounding in a forgotten account, the accumulation of uncertainty is guaranteed to eventually become significant. After a hundred million years, which is much less than the 4.5 billion year age of the solar system, the position of Earth in its orbit becomes completely impossible to predict. For times 100 million years in the future, we have no firm knowledge of Earth’s trajectory. We have no idea whether January 1, 100,000,000 AD will occur in the winter or in the summer, or even whether Earth will be orbiting the Sun at all.
Poincaré’s great insight was that the realistic physical description of non-trivial systems can involve what we now call chaotic behavior. The weather is an excellent example. Overnight weather forecasts are generally quite accurate. Three-day forecasts are certainly of some utility. Two-week forecasts, on the other hand, are essentially worthless. Although we have a very clear understanding of the laws of physics that govern the behavior of Earth’s atmosphere, we can’t sample global weather conditions with enough precision to make forecasts accurate beyond a few days. If you let out a deep sigh at the complexity of it all, then the air current that you exhale will spur subtle deviations in the flow of air and moisture of the Earth’s surface that become increasingly magnified over time. The aggravated swirl of air from a slap at a mosquito can career into divergences that visit a hurricane on Miami rather than spinning it out into oblivion over the North Atlantic. Although we can’t accurately predict how the pattern of weather fronts and daily high temperatures will look on the 10:00 p.m. News two weeks from today, we do have some idea of what the weather will be. If it is in the middle of the summer, Texas will be hot. Duluth, in January, will be cold. The pattern of erratic day-to-day weather is superimposed over solidly predictable seasonal and regional climates.
We can thus ask the question: Are the movements of the planets predictably chaotic in the same sense as the weather? That is, over billions of years, will the planets wander only within circumscribed bounds, or is a more wild chaos, with orbit crossing, ejections, collisions and the like – a real possibility?
The answer will be a statistical statement. To high probability, the planets will remain more or less on their present courses until the Sun becomes a red giant. Exactly how high a probability is not fully clear. Stay tuned…
