Image Source.
The academic quarter is pulling up to the half-way point at UCSC, and it’s getting tougher to keep up with everything that I’m supposed to do. I’ve been spending a lot of time getting the lectures together, so in the interest of sticking to a schedule of posts, I thought I’d veer from the all-planets-all-the-time approach and show some scanned transparencies from Friday’s class.
The orbit of an idealized planet around an idealized star is a keplerian ellipse. A planet on an elliptical trajectory conserves its eccentricity, orbital period, longitude of periastron, inclination, and line of nodes. The only orbital element that changes over time is the mean anomaly. We can thus say that the Keplerian orbit contains five integrals (constants) of the motion.
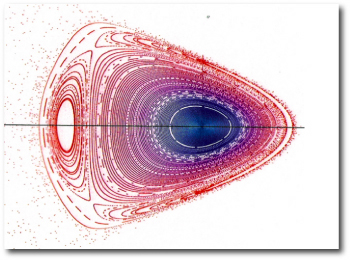
If the potential arises from a mass distribution that’s not a perfect point mass, then in general we won’t have five integrals of motion. It’s interesting to look at a subsection of the weird variety of planar orbits that occur in a two-dimensional potential distribution that looks like this:
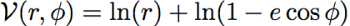
The ln(r) term causes this potential goes to negative infinity at the origin while remaining unbounded at large radii. The second term, in which e is specified to take on values between 0 and 1, lends a modulation that makes the force law non-axisymmetric with respect to the origin. One can roughly think of orbits in this potential as the motion of a marble rolling in a funnel-shaped, lopsided bowl.
The potential function does not change with time, and so the energy of an orbiting particle is conserved. Further, because of the self-similarity of the potential, the structure of orbits at one energy will be an exact copy of the orbit structures at all other energies. Thus, there’s no loss in generality by sampling orbits having only a single total energy (kinetic + potential). In the following sampler of pictures, I integrate the trajectories of single particles launched from the long (+x) axis of the potential with initial velocities always perpendicular to the long axis. The magnitude of the velocities are determined by the total energy choice: particles starting closer to the origin must have a higher initial kinetic energy to offset their more negative gravitational potential energy. I also vary the parameter e.
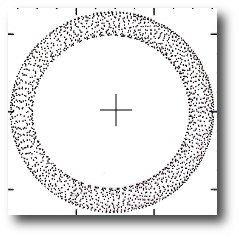
For e=0.2 and an initial position x=0.78, the orbit is reasonably circular, and steady precession smears the excursion of the particle over many orbits into a thin annular region centered on the origin.
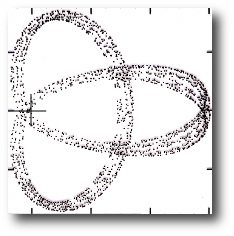
For e=0.42, x=0.55, the particle starts fairly close to its zero velocity curve. It thus falls inward almost to the origin before making a second loop, and then a second approach to the origin which sends it rocketing back up close to its initial position.
Taking e=0.2, x=0.78 leads to a single loop orbit that dives in very close to the origin.

Here’s the result of taking e=0.42 and x=0.55. It’s a good thing the Earth isn’t orbiting in this potential with these particular starting conditions.

This one, which arises from e=0.81 and x=0.85 is pretty cool. Most of the time it runs counterclockwise as viewed from above, but before close approach to the origin it switches to clockwise. One’s tempted to classify it as an Enron orbit. From all appearances it appears to be clocking a steady increase in angle, whereas in reality, when the books are finally audited, it’s accumulating -2pi radians every period.

Choosing e-0.30, x=0.03 launches the particle on a highly chaotic trajectory. This orbit is uniformly sampling the entire area allowed to it by its total energy constraint.

For larger values of the e parameter the orbits often show a fundamentally different behavior. Choosing e=0.72, x=0.22 leads to a motion which is restricted to oscillations of a narrow angular range centered on the long-axis of the potential. The particle is basically rolling back and forth in the narrow valley provided by the high-e potential.
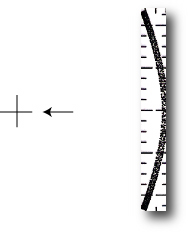
e=0.90, x=0.20 gives an orbit with a similar quality:

Hi everyone,
Although weird potentials and weird orbits can appear in planetary dynamics, they are very prevalent in galactic dynamics. You can look through “Galactic Dynamics” by Binney & Tremaine (1994, Princeton University Press) for examples of
weirdness.
Eugenio
You can look at the Sloan Digital Sky Survey for real weirness!
Pingback: systemic - zoom