
Image Source.
Chalk another transiting exo-planet up on the board. In a preprint released today, Gaspar Bakos and his colleagues in the HATnet project are announcing HAT-P-1b, a large-radius, low-density planet transiting one member of a relatively nearby, relatively bright solar-type binary star.
HAT-P-1b (which orbits the star BD+37 4734) is quite interesting for several reasons. Its 4.46529 day orbit is the longest period yet detected for a transiting extrasolar planet, and its measured radius of 1.36 Jupiter radii is alarmingly larger than the baseline theoretical prediction. The planet contains 0.53 Jupiter Masses, and has a surface temperature near 1100 K, so our models predict that it should have a radius of 0.94 Jupiter radii if it contains a 20 Earth-mass heavy-element core, and a radius of 1.09 Jupiter radii if it’s made of pure solar-composition gas. It’s thus roughly 20-30% larger than it “should” be, which means that something is providing it with a very significant source of extra interior heat.
The large radius of the planet means that the transits exhibit a ~1.5% photometric depth. Deep transits make it easier to obtain data with high signal-to-noise, which means that we can look forward to very accurate follow-up measurements for this system. The presence of a nearly identical companion star at a separation of 11 arc seconds should also help observers obtain good differential photometry. The star is up now, and its well-placed for Northern Hemisphere observers. I don’t think it’ll be long before we see confirmations rolling in from small-telescope observers worldwide. If you’re interested in observing it, the ephemeris table is here.
Where could the extra source of heat be coming from? One possibility is tidal dissipation related to the circularization of an eccentric orbit.
The theory of tides can rapidly slip into thousands of pages of detailed mathematical analysis. Many of the interesting ideas, however, are close to the surface. In the introduction to his still-useful 1898 popular book, “The Tides”, Sir George H. Darwin, the son of the naturalist, and Plumian Professor at Cambridge, wrote:
A mathematical argument is, after all, only organized common sense, and it is well that men of science should from time to time explain to a larger public the reasoning behind their mathematical notation. To a man unversed in popular exposition it needs a great effort to shell away the apparatus of investigation and the technical mode of speech from the thing behind it.
I would actually argue that the situation is quite the opposite. I think it’s easier and better to get a colloquial, heuristic understanding first, and then make an attempt to put the ideas on a sound mathematical basis.
For a planet that (like Hat-P-1b) has an orbital period of less than a month or so, it’s expected that tidal forces will rapidly bring the planet into synchronous rotation, in which the planet spins once on its axis every orbital period. For a circular orbit, this means that the planet always keeps one face to the star, just as the Moon keeps one side toward the Earth. If the orbit is eccentric, however, the planet will not manage to keep one side directly facing the star. Because the planet spends more time at the far point of its orbit, it does more “turning” there, and remarkably, it turns out that the planet always keeps one face pointed toward the empty focus of its elliptical orbit. From the point of view of the star, a fixed point on the planet is seen to librate. The Moon’s orbit is slightly eccentric, and so we can see this effect in time-lapse animations of lunation. See here and also (if you’re not inclined to motion sickness, here).
The tidal bulge of the planet, on the other hand, is forced to always point toward the star, as it’s the star’s gravity that is producing the differential gravitational attraction. This means that once per orbit, the tidal bulge is rocked back and forth across the planet, which produces serious internal heating. The size of the bulge also increases and decreases once per orbit due to the varying distance between the planet and the star, and the resulting oscillation also contributes to the amount of internal tidal heating.
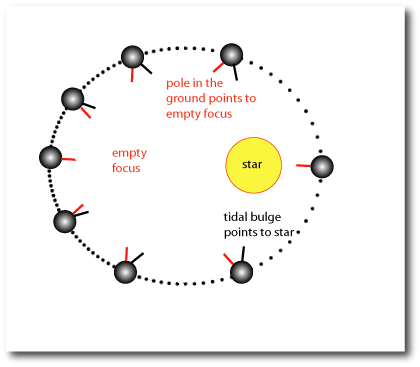
The amount of tidal energy deposited in the planet increases with the square of the orbital eccentricity. A reasonable model for the physical properties of HAT-P-1b indicates that an eccentricity e=0.09 is adequate to generate enough tidal heating to expand the planet to its observed size of 1.36 Jupiter radii. The problem, is that the orbit should circularize on a timescale of less than 1 billion years, whereas the system seems to be about 4 billion years old. Therefore, if a significant orbital eccentricity exists, then there must be a mechanism to maintain the eccentricity. The best candidate is another planet further out in the system.
We can take a quick look to see whether such a situation holds water. A second planet in the system will exert gravitational perturbations of HAT-P-1b, which will cause its eccentricity to vary with time. The picture to have in one’s head is to imagine that the planets are viewed on a timescale that is much longer than an orbital period. If one takes the long view, the motion of the planet is effectively blurred out along the orbit, and one can model the planet as an elliptical wire of varying mass density — heavy near apastron where more time is spent, and light near periastron where the planet spends less time. The interaction between the two planets can then be modeled as the interaction between two flexible elliptical wires. When one does this, and ignores the moment-by-moment motion of the planet, one is making a “secular approximation”. Secular theory was developed to a high art in the 1770s by Laplace and Lagrange, and we can make use of their work to quickly look at how the eccentricities of two mutually interacting planets vary with time.
Over at the transitsearch.org, I have a program which computes a 2nd-order secular theory for each of the known multiple-planet systems, and plots the resulting eccentricity variations as part of the candidate information table . (To see the plots of the secular variations, click on the “planet column” for a multiple planet system such as Upsilon Andromedae).
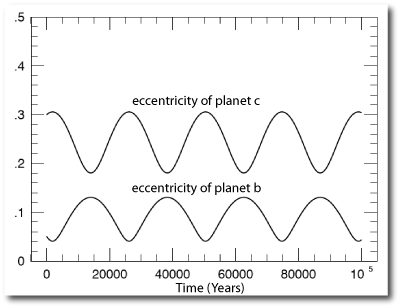
An advantage of using the secular approximation to the dynamics is that one can quickly scan through a range of planet-planet configurations and find out what the perturbative interactions look like. If I add a second planet to the HAT-P-1 system with a period of 50 days, a mass of 0.06 Jupiter masses, and an orbital eccentricity of e=0.30, I get the following long-term variation in eccentricities, in which the eccentricity of planet b has a time-averaged value close to e=0.09:
Is it possible to hide a second planet in the system while remaining consistent with the (still sparse) set of published radial velocity measurements? The downloadable console is ideally suited to quickly answering such a question. It turns out that it’s very easy to get a perfectly adequate 2-planet fit to the data in which a hypothesized perturbing outer planet is capable of maintaining a time-averaged eccentricity e=0.09 for the inner planet. One such fit looks like this:
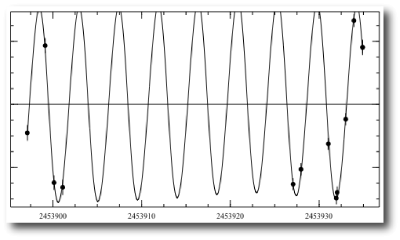
corresponding to a system configuration that looks like this:
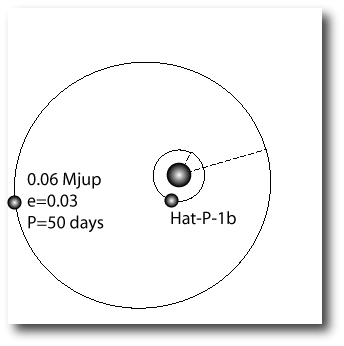
It would be exciting if a planet like the one in the above diagram (or its dynamical equivalent) could be detected. This would tell us that we’re on the right track in obtaining a better understanding of the wide range of observed radii among the known transiting planets. Probably the fastest way to detect the perturbing planet is through accurate timing of the intervals between successive transits. If an outer planet is tugging on the inner planet, then the orbit will fail to be perfectly periodic, and variations will be observed in the amount of time that passes between transits. Matt Holman and Norm Murray have written a paper that describes how this works. They give a rule-of-thumb equation for the transit-to-transit variations that one can expect. For a planet similar to HAT-P-1b, with semimaor axis a1 and period P1, and a pertubing planet with simimajor axis a2 (where a2>a1), period P2 and mass M2, they find that the typical variation of the interval between successive transits is given by
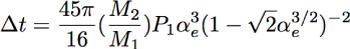
where

For HAT-P-1b and HAT-P-1c (as hypothesized above) delta T works out to about 5 seconds. Variations of this magnitude are readily detected from the ground, and a number of research groups will probably jump right on this problem.

Drake Deming just wrote to say that there’s a typo on the Holman-Murray equation, and that the factor in front is 16/(45 pi). This would bring the time difference Delta T down by close to a factor of 10, and will make the timing differences quite a bit tougher to detect. Over the weekend, I’ll integrate my model system, and get the exact timing discrepancy numbers for the hypothetical 2-planet system described in the post.
-Greg
Pingback: systemic - lightcurves
Pingback: systemic - hot and bothered
Pingback: systemic - Another HAT trick