This post continues the oklo.org posts: (1) the black cloud, and (2) disks.

There are two competing, completely distinct theories that describe how a giant planet like Jupiter can be generated from a protostellar disk of gas and dust. The first theory, formation via gravitational instability, lends itself to large-scale hydrodynamical simulations and extraordinary animations that can be downloaded over the Internet. It’s an easy theory to grasp. The second theory, formation via core accretion, presents a more complicated chain of events, but nevertheless contains the story that seems (in my opinionated opinion) to be most nearly correct. Let’s look at what these two theories say, and let’s examine the evidence in favor of and against each.
In the gravitational instability picture, the outer lagging remnants of the molecular cloud core fall in and land on the protostellar disk, causing it to grow in mass. As the disk mass increases, it begins to be influenced by its own gravity. That is, it starts to feel a tendency to fragment in response to its own weight. Simultaneously, the pressure of the gas in each nascent fragment pushes back and partially offsets the fragment’s inclination toward collapse. Pressure thus acts as a small-scale stabilizing influence against collapse. In addition, the differential rotation of the disk (material closer to the star orbits faster) tries to sheer a growing fragment apart. Differential rotation thus acts as a large-scale stabilizing influence against gravitational collapse.
The question boils down to the following: Does gravity win, allowing a Jupiter-mass planet to rapidly form as a condensation in the disk, or do shear and pressure win, keeping the disk free of giant-planet fragments?
The situation lies within the general framework of a linearized hydrodynamical stability analyses, and can be analyzed mathematically. The analysis leads to a so-called stability criterion, the famous Toomre Q:
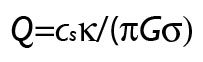
Where c_s is the sound speed in the disk, kappa is the epicyclic frequency, G is Newton’s gravitational constant, and sigma is the disk surface density. If Q<1 at any radius in the disk, then the disk is unstable with respect to m=0 (ringlike) disturbances. If Q is slightly greater than 1, computer simulations show that the disk is prone to strong non-axisymmetric instabilities, and hence experiences exponential growth of disturbances and eventual fragmentation.
As with any seemingly abstruse physical phenomenon, The disk instability analysis can be illuminated with an analogy. In this case, the appropriate analogy involves a rock band, a house party, kegs of free beer, and uninvited punks and thugs.
Neophyte rock bands need to attract audiences for their shows. Hence, they need to provide inducements. Free beer does the trick. Free beer, or more precisely, flyers posted all over a college campus advertising a party serving free beer, act in analogy to the self-gravity of a disk. As I have discovered (through direct experience, back in my reckless, rock-band fronting youth), such a course of action can lead to instability. If you flyer a campus with news of free kegs, then dozens to hundreds of punks and thugs, whom no-one has ever seen before, and whom no-one wants to see again, will descend upon the hapless band’s house-party show. Amplifiers are destroyed. Holes are kicked in sheetrock. The cops show up, and the band does not play. This outcome can be profitably compared to a disk that undergoes a gravitational collapse into Jovian-mass fragments.

[Above: Our bass player (at a show of ours that was shut down by the cops after several songs). He later graduated with a Ph.D. in Physics, after defending his dissertation on 2D quantum black holes.]
In practice, however, the police do not always show up at house-party shows. Sometimes, the band gets to play. This happier outcome is abetted by two stabilizing effects. Just as in the case of the disk gravitational instability, one of these stabilizing effects operates on large scales, and the other operates on small scales. On the large scale, one can create an analog of “differential rotation†with a lack of specificity on the flyers regarding the precise time of the show. Punks drift in. They see that they don’t particularly like how the band sounds. They see the long lines to the kegs. They drift away. The band plays its entire set to a modest audience, and the cops don’t show up. Support on small scales, the analog of “pressure†is provided by a quite different effect: body odor. The thugs that show up invariably smell poorly, and the unpleasantness associated with a sweaty throng of them will drive some away. If the pressure is high enough, that is, if the thugs smell badly enough, then the show proceeds, and instability is again averted.
For readers familiar with the linearized analysis that leads to the Toomre Q criterion, here’s an illustration of how the analogy can be applied to the standard WKB dispersion relation:
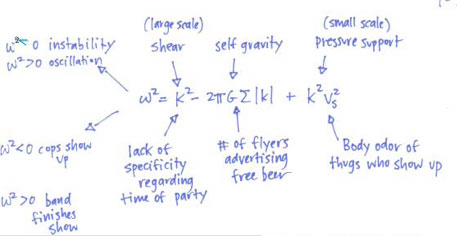
In a future post in this series, we’ll explain why the weight of observational and theoretical evidence seems to be shifting against the gravitational instability hypothesis. The computer simulations, which become ever more impressive with each inexorable tick of Moore’s law, show that in order for fragments to form and then last as planets, the rate of cooling in the disk must be extremely efficient. Rapid cooling robs a nascent fragment of its ability to produce pressure, and hence permits gravitational collapse. Perhaps more importantly, the computer simulations also show that a disk will suffer from a whole panoply of instabilities before its mass grows large enough to trigger the full-blown collapse of Jupiter-like planets.
These instabilities take the form of spiral waves of the same type that occur in spiral disk galaxies such as M51, shown in the HST photo at the top of the post. In a protostellar disk, the spiral wave action pushes pulse after pulse of gas out of the regions of the disk that are in the most danger of fragmenting directly into planets. Some of this gas is forced to large distances from the central star, while the majority flows inward and eventually winds up on the star. In all likelihood, most protoplanetary disks manage to avoid direct fragmentation.


Pingback: systemic - G.I. No
Pingback: systemic - Lonely Planet Guide to the Hyades
Pingback: Centauri Dreams » Blog Archive » Hyades Planet Challenges Formation Theories